Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Ôn tập chương 1: Hệ thức lượng trong tam giác vuông chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Ôn tập chương 1: Hệ thức lượng trong tam giác vuông
a) ;
b) ;
c)
Phương pháp giải:
Áp dụng kiến thức:
1)
2)
Lời giải:
a)
* Ta có:
Suy ra:
Vì nên
*
b)
* Ta có:
Suy ra:
Vì nên
*
c)
* Ta có:
Suy ra:
Vì nên
*
a) ;
b) ;
c) ;
d) ;
e) ;
g) ;
h) ;
i)
Phương pháp giải:
Áp dụng các kiến thức:
1)
2)
Lời giải:
a)
b)
c)
d)
g)
i)
Lời giải:
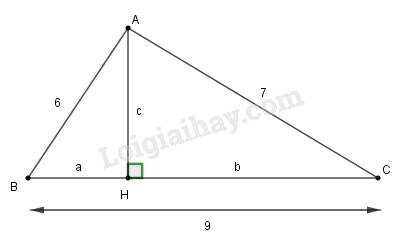
Gọi độ dài đường cao là , hình chiếu của hai cạnh và trên cạnh có độ dài bằng lần lượt là và .
Ta có: ( vì )
Theo định lí Pi-ta-go, ta có:
Suy ra:
Mà (*) nên:
Thay vào (*), ta có:
Suy ra:
cạnh bên có độ dài là 6.
Phương pháp giải:
Áp dụng tính chất về cạnh và đường cao của tam giác cân.
Vận dụng định lí Py-ta-go vào các tam giác vuông.
Lời giải:
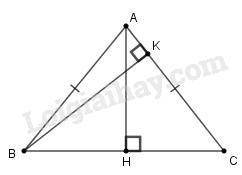
Giả sử cân tại có
Vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến. Suy ra (tính chất tam giác cân)
Suy ra:
Áp dụng định lí Pi-ta-go vào tam giác vuông , ta có:
Từ (1) và (2) suy ra:
Suy ra:
Vậy
a) Chứng minh:
b) Chứng minh đồng dạng
c) Tính tổng bằng hai cách
Cách 1: Sử dụng kết quả ở câu b);
Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.
Phương pháp giải:
- Áp dụng định lí Py-ta-go trong tam giác vuông.
- Các trường hợp bằng nhau của tam giác.
- Sử dụng: Trong tam giác ABC vuông tại A thì
Lời giải:
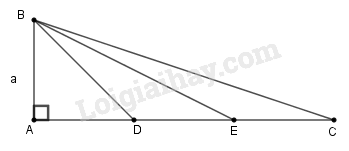
a) Ta có:
Áp dụng định lí Pi-ta-go vào tam giác vuông , ta có:
Suy ra:
Ta có:
Vậy
b) Xét và , ta có:
(1)
(2)
Từ (1) và (2) suy ra đồng dạng (c-g-c).
c) * Cách 1:
Ta có: đồng dạng
Mặt khác:
(3)
Trong , ta có:
(tính chất góc ngoài) (4)
Lại có: (vì ∆ABD vuông cân tại A) (5)
Từ (3), (4) và (5) suy ra:
* Cách 2:
Ta có:
Trong tam giác , ta có:
Suy ra:
Trong tam giác vuông , ta có:
Suy ra:
Suy ra
Vậy
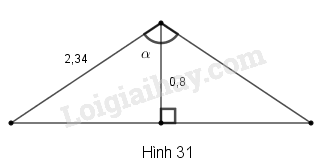
Vận dụng kiến thức :
Trong tam giác ABH vuông tại H thì , từ đó tìm độ lớn góc .
Lời giải:
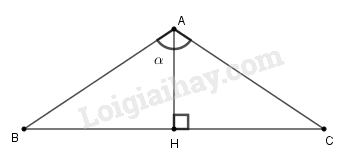
Hai mái nhà bằng nhau tạo thành hai cạnh AB, AC của một tam giác cân ABC (hình vẽ). Chiều cao AH của tam giác ABC cũng là đường phân giác của tam giác. Khi đó ta có:
Xét tam giác ABH vuông tại H, ta có:
Bấm máy tính: SHIFT cos 0,3419 =
Suy ra:
Vậy .
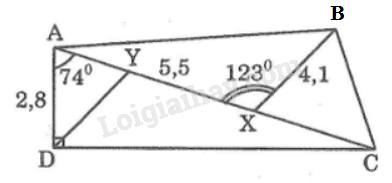
Biết:
;
a) Tính .
b) Gọi là điểm trên sao cho . Hãy tính
c) Tính diện tích tam giác .
Phương pháp giải:
Áp dụng các hệ thức lượng trong tam giác vuông.
Lời giải:
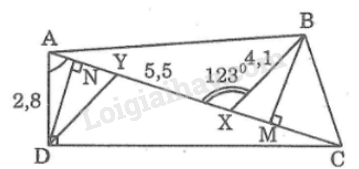
a) Trong tam giác vuông ACD, ta có:
b) Kẻ
Trong tam giác vuông , ta có:
Vì nên ( hai góc so le trong)
Mà (kề bù)
Suy ra:
Trong tam giác vuông , ta có:
Ta có:
c) Ta có:
Kẻ
Ta có:
Trong tam giác vuông BMX, ta có:
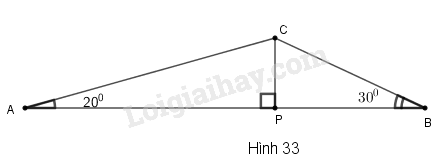
Hãy tìm:
a) AP, BP;
b) CP.
Phương pháp giải:
Áp dụng kiến thức về hệ thức lượng trong tam giác vuông.
cot = cạnh kề : cạnh đối.
Lời giải:
a) Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
Từ (1) và (2) suy ra:
Hay
Suy ra:
b) Thay vào (1) ta có:
Thay vào (2) ta có:
Phương pháp giải:
Áp dụng tỉ số giữa cạnh kề và cạnh đối trong tam giác vuông.
Lời giải:
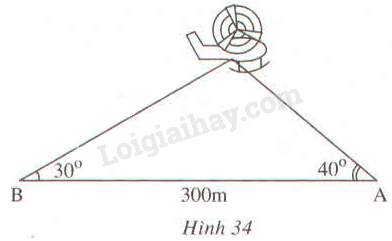
Gọi là vị trí của máy bay.
Kẻ
Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
Từ (1) và (2) suy ra:
Hay
Suy ra:
- Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
- Chu vi hình thang bằng tổng độ dài các cạnh bao quanh của hình đó.
- Diện tích hình thang bằng đáy lớn cộng đáy bé (cùng đơn vị đo) chia 2 rồi nhân với chiều cao.
Lời giải:
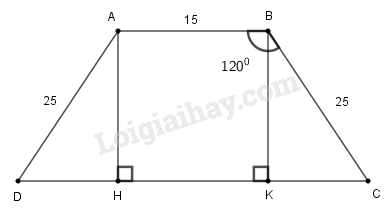
Giả sử hình thang có đáy nhỏ , cạnh bên , .
Kẻ
Ta có: và (cùng vuông với CD) nên là hình bình hành.
Suy ra: và
Vì AB//CD nên (hai góc trong cùng phía)
Suy ra:
Trong tam giác vuông , ta có:
Ta có: (cmt) và (gt) nên hai tam giác vuông (cạnh huyền - cạnh góc vuông)
Suy ra:
Ta có:
Chu vi hình thang là:
Diện tích hình thang là:
a) Tính ;
b) Phân giác của góc cắt tại . Tính .
c) Từ kẻ và lần lượt vuông góc với và . Tứ giác là hình gì? Tính chu vi và diện tích của tứ giác .
Phương pháp giải:
a) Áp dụng định lí Py-ta-go và tỉ số lượng giác.
b) Vận dụng tính chất đường phân giác tìm độ dài cạnh BD.
c) Áp dụng dấu hiệu nhận biết các hình tứ giác đã học.
Tính chu vi và diện tích của tứ giác.
Lời giải:
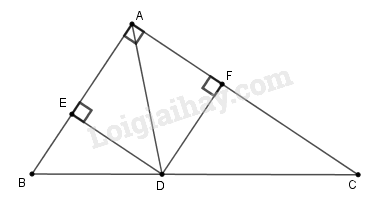
a) Áp dụng định lí Pi-ta-go vào tam giác vuông , ta có:
Suy ra:
Xét tam giác vuông ABC, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
Suy ra:
Ta có: (vì tam giác ABC vuông tại A)
b) Vì AD là đường phân giác của tam giác ABC, nên:
(tính chất đường phân giác)
Suy ra:
Suy ra:
c) Ta có:
Suy ra tứ giác có ba góc vuông nên hình đó là hình chữ nhật.
Mặt khác, nằm trên tia phân giác của góc nên (tính chất tia phân giác của 1 góc)
Vậy tứ giác là hình vuông.
Vì nên
Theo định lí Ta-lét trong tam giác BAC, ta có:
Chu vi tứ giác bằng:
Diện tích tứ giác bằng:
a) Tính
b) Tính chiều cao của hình thang .
Phương pháp giải:
a) Áp dụng định lí Py-ta-go và tỉ số lượng giác.
b) Chiều cao hình thang ABCD bằng chiều cao tam giác ABC, áp dụng tỉ số lượng giác, tìm chiều cao của tam giác ABC.
Lời giải:
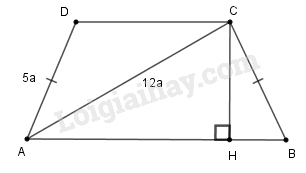
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
Suy ra:
Xét tam giác vuông ABC, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
Suy ra:
b) Kẻ
Trong tam giác vuông , ta có:
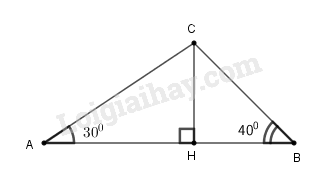
a) Tính các góc của tam giác .
b) Tính diện tích tứ giác .
Phương pháp giải:
a) Áp dụng tỉ số lượng giác của góc nhọn và định lí Py-ta-go vào các tam giác vuông.
b) Áp dụng định lí Py-ta-go và kiến thức về đường trung bình của tam giác.
Lời giải:
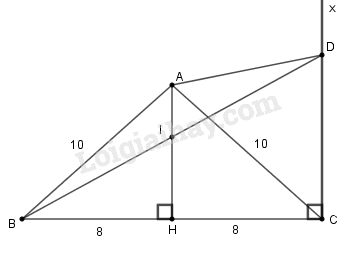
a) Vì tam giác ABC cân tại A có nên AH cũng là đường trung tuyến, suy ra:
Trong tam giác vuông , ta có:
Suy ra:
Vì cân nên
Ta có: (tổng 3 góc trong tam giác ABC)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:
Suy ra:
Ta có:
Suy ra:
Vì và nên (1)
Mặt khác: (cmt) (2)
Từ (1) và (2) ta có là đường trung bình của tam giác .
Suy ra: hay
Ta có:
Vì nên AHCD là hình thang và nên HC là chiều cao của hình thang AHCD. Từ đó:
Vậy (cm2)
a) Chứng minh tam giác vuông.
b) Tính sinB, sinC.
Phương pháp giải:
a) Áp dụng định lí Py-ta-go đảo.
b) Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải:
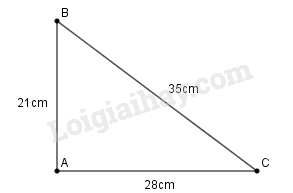
a) Ta có:
Vì nên tam giác vuông tại ( theo định lí đảo Pi-ta-go).
b) Xét tam giác ABC vuông tại A, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
a) Chứng minh
b) Tính tỉ số diện tích tam giác DBC và diện tích hình thang ABCD.
c) Tính tỉ số diện tích tam giác ABC và diện tích tam giác BCD.
Phương pháp giải:
Vận dụng kiến thức :
- Tứ giác có ba góc vuông và hai cạnh kề bằng nhau là hình vuông.
- Công thức tính diện tích tam giác và hình thang.
- Tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải:
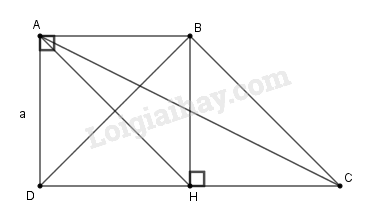
a) Kẻ
Ta có: nên (hai góc trong cùng phía bù nhau) và (gt)
Suy ra:
Từ đó, tứ giác có ba góc vuông nên là hình chữ nhật. Mà nên là hình vuông.
Suy ra:
Ta có:
Suy ra:
Vậy
b) Ta có: (đvdt)
(đvdt)
Vậy
c) Diện tích tam giác vuông tại là: (đvdt)
Mà (theo câu b)
Ta có: (đvdt)
Vậy
(với đvdt: đơn vị diện tích)
a) Tính độ dài đường phân giác .
b) Gọi là trung điểm của . Chứng minh
Phương pháp giải:
- Vận dụng định lí Ta-lét trong tam giác.
- Chứng minh tam giác cân tại .
Lời giải:
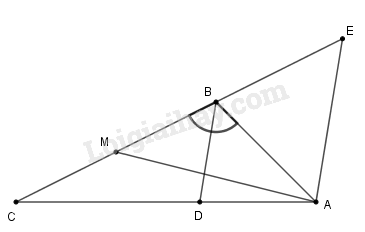
a) Vì BD là tia phân giác của góc ABC nên:
Từ kẻ đường thẳng song song với cắt tại .
Lại có:
(so le trong)
(đồng vị)
Suy ra tam giác đều (vì có 2 góc bằng )
Khi đó:
Tam giác có nên theo hệ quả định lý Ta-lét ta suy ra:
b) Vì M là trung điểm cạnh BC nên ta có:
Từ (1) và (2) suy ra:
cân tại .
Tam giác cân có là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy
a) Tính độ dài đoạn thẳng .
b) Các đường thẳng vuông góc với tại và tại lần lượt cắt tại và . Chứng minh là trung điểm của và là trung điểm của .
c) Tính diện tích tứ giác .
Phương pháp giải:
a) Áp dụng tính chất hình chữ nhật và hệ thức lượng giữa đường cao và hình chiếu trong tam giác vuông.
b) Áp dụng tính chất của hình chữ nhật và tam giác cân.
c) Nhẩm lại dấu hiệu nhận biết hình thang và cách tính diện tích của hình đó.
Lời giải:
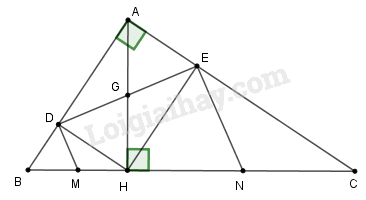
a) Ta có:
Tứ giác có góc vuông nên nó là hình chữ nhật.
Suy ra: (tính chất hình chữ nhật)
Tam giác vuông tại và có là đường cao.
Theo hệ thức liên hệ giữa đường cao và hình chiếu ta có:
Vậy
b) * Gọi là giao điểm của và
Ta có: (tính chất hình chữ nhật ADHE)
Suy ra tam giác cân tại
Ta có:
Từ (1), (2) và (3) suy ra:
Suy ra tam giác cân tại
Lại có:
( vuông tại ) (7)
Từ (4), (6) và (7) suy ra:
Suy ra tam giác cân tại
Từ (5) và (8) suy ra: hay là trung điểm của .
*Tam giác cân tại (do (cmt))
Ta có:
(10)
(11)
Từ (9), (10) và (11) suy ra: (12)
Suy ra tam giác cân tại (13)
Lại có: (14)
( vuông tại ) (15)
Từ (12), (14) và (15) suy ra:
Suy ra tam giác cân tại
Từ (13) và (16) suy ra: hay là trung điểm của .
c) Tam giác vuông tại có là đường trung tuyến nên:
Tam giác CEH vuông tại E có EN là đường trung tuyến nên
Mà và nên
Suy ra tứ giác là hình thang
Vậy
a) Tính
b) Từ kẻ lần lượt vuông góc với các đường phân giác trong và ngoài của góc .
Chứng minh: và
c) Chứng minh hai tam giác và đồng dạng. Tìm tỉ số đồng dạng.
Phương pháp giải:
Vận dụng kiến thức :
a) Tỉ số lượng giác của góc nhọn trong tam giác vuông.
b) Dấu hiệu nhận biết và tính chất của hình chữ nhật.
c) Các trường hợp đồng dạng của tam giác.
Lời giải:
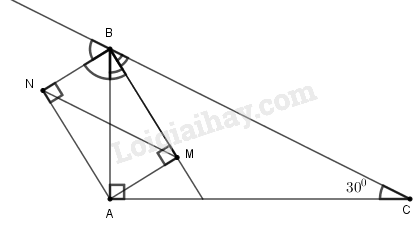
a) Trong tam giác vuông , ta có:
b) Ta có:
(hai tia phân giác của 2 góc kề bù thì vuông góc với nhau)
(gt)
(gt)
Từ (1), (2) và (3) suy ra tứ giác là hình chữ nhật.
Suy ra (tính chất hình chữ nhật)
Suy ra: (c.g.c)
Mà
Suy ra:
Suy ra (có cặp so le trong bằng nhau)
Vì là hình chữ nhật nên .
c) Tam giác vuông tại nên
Suy ra:
Suy ra:
Xét hai tam giác và , ta có:
Suy ra đồng dạng với (g.g)
Tỉ số đồng dạng:
a) Chứng minh tam giác vuông tại . Tính các góc và đường cao của tam giác.
b) Tìm tập hợp các điểm sao cho
Phương pháp giải:
a) Áp dụng định lí Pi-ta-go đảo và tỉ số lượng giác.
b) Dựa vào diện tích của các hình tam giác và để biện luận.
Lời giải:
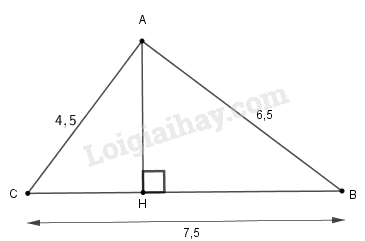
a) Ta có:
Vì nên tam giác vuông tại ( theo định lí Pi-ta-go đảo).
Kẻ . Xét tam giác ABC vuông tại A, theo hệ thức lượng trong tam giác vuông, ta có:
Áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác ABC vuông, ta có:
Suy ra:
Ta có:
(vì tam giác ABC vuông tại A)
b) Tam giác và tam giác có chung cạnh đáy , đồng thời nên khoảng cách từ đến bằng khoảng cách từ đến . Vậy thay đổi cách một khoảng bằng nên nằm trên hai đường và song song với cách một khoảng bằng .
a) đồng dạng ;
b)
Phương pháp giải:
Áp dụng kiến thức về hai tam giác đồng dạng và tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải:
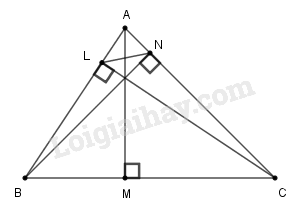
a) Xét hai tam giác và , ta có:
chung
Suy ra đồng dạng (g.g)
Suy ra:
Xét hai tam giác và , ta có:
chung
Suy ra đồng dạng (c.g.c)
b) vuông tại nên
vuông tại nên
vuông tại nên
Từ (1), (2) và (3) suy ra: