Với giải Bài 36 trang 94 Toán lớp 9 chi tiết trong Ôn tập chương I Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9: Ôn tập chương I Hình học

Bài 36 trang 94 Toán lớp 9 tập 1: Cho tam giác có một góc bằng ${45}^0$. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hình 46 và hình 47).

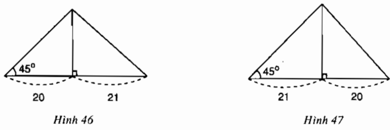
Lời giải:

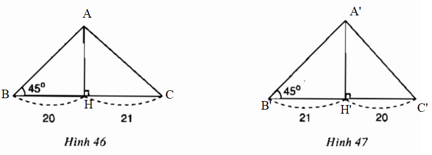
*Trường hợp hình 46:

Xét tam giác ABH vuông tại H

Áp dụng định lí Py-ta-go ta có:

${\mathrm{AB}}^2={\mathrm{BH}}^2+{\mathrm{AH}}^2$

Xét tam giác ACH vuông tại H

Áp dụng định lí Py-ta-go ta có:

${\mathrm{AC}}^2={\mathrm{CH}}^2+{\mathrm{AH}}^2$ (1)

Ta có: BH < CH (do 20cm < 21cm)

$$\begin{gathered} \Rightarrow {\mathrm{BH}}^2<{\mathrm{CH}}^2 \\ \Rightarrow {\mathrm{AB}}^2<{\mathrm{AC}}^2 \\ \Rightarrow \mathrm{AB}<\mathrm{AC} \end{gathered}$$

Do đó cạnh lớn hơn là AC

Xét tam giác ABH vuông tại H

$$\begin{gathered} \widehat{\mathrm{AHB}}={90}^{\mathrm{o}} \\ \widehat{\mathrm{ABH}}={45}^{\mathrm{o}} \\ \Rightarrow \widehat{\mathrm{BAH}}={90}^{\mathrm{o}}-{45}^{\mathrm{o}}={45}^{\mathrm{o}} \end{gathered}$$

Do đó tam giác ABH vuông cân tại H (hai góc ở đáy $\widehat{\mathrm{ABH}}=\widehat{\mathrm{BAH}}={45}^{\mathrm{o}}$)

$\Rightarrow \mathrm{AH}=\mathrm{BH}=20\mathrm{cm}$

Từ (1) ta có: ${\mathrm{AC}}^2={\mathrm{CH}}^2+{\mathrm{AH}}^2={21}^2+{20}^2=841$

$\Rightarrow \mathrm{AC}=\sqrt{841}=29$ (cm)

*Trường hợp hình 47:

Áp dụng định lí Py-ta-go ta có:

${\mathrm{AB}}^2={\mathrm{BH}}^2+{\mathrm{AH}}^2$ (2)

Xét tam giác ACH vuông tại H

Áp dụng định lí Py-ta-go ta có:

${\mathrm{AC}}^2={\mathrm{CH}}^2+{\mathrm{AH}}^2$

Ta có: BH > CH (do 21cm > 20cm)

$$\begin{gathered} \Rightarrow {\mathrm{BH}}^2>{\mathrm{CH}}^2 \\ \Rightarrow {\mathrm{AB}}^2>{\mathrm{AC}}^2 \\ \Rightarrow \mathrm{AB}>\mathrm{AC} \end{gathered}$$

Do đó cạnh lớn hơn là AB

Xét tam giác ABH vuông tại H

$$\begin{gathered} \widehat{\mathrm{AHB}}={90}^{\mathrm{o}} \\ \widehat{\mathrm{ABH}}={45}^{\mathrm{o}} \\ \Rightarrow \widehat{\mathrm{BAH}}={90}^{\mathrm{o}}-{45}^{\mathrm{o}}={45}^{\mathrm{o}} \end{gathered}$$

Do đó tam giác ABH vuông cân tại H (hai góc ở đáy $\widehat{\mathrm{ABH}}=\widehat{\mathrm{BAH}}={45}^{\mathrm{o}}$)

$\Rightarrow \mathrm{AH}=\mathrm{BH}=21\mathrm{cm}$

Từ (2) ta có:

$$\begin{gathered} {\mathrm{AB}}^2={\mathrm{BH}}^2+{\mathrm{AH}}^2={21}^2+{21}^2=882 \\ \Rightarrow \mathrm{AB}=\sqrt{882}=21\sqrt{2} \end{gathered}$$