Với lời giải SBT Toán 10 trang 8 Tập 2 chi tiết trong Bài 15: Hàm số sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 15: Hàm số

Bài 6.5 trang 8 SBT Toán 10 Tập 2: Trong một cuộc thi chạy 100 m, có ba học sinh dự thi. Biểu đồ trên Hình 6.9 mô tả quãng đường chạy được y (m) theo thời gian t (s) của mỗi học sinh.

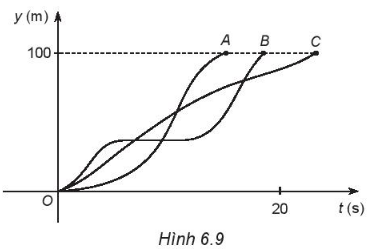
a) Đường biểu diễn quãng đường chạy được của mỗi học sinh có là đồ thị hàm số hay không?

b) Học sinh nào về đích đầu tiên? Hãy cho biết ba học sinh đó có chạy hết quãng đường thi theo quy định hay không.

Lời giải:

a)

Xét đường biểu diễn quãng đường chạy được của mỗi học sinh, với mỗi giá trị của t (s) ta chỉ nhận được một giá trị của s (m) tương ứng, do đó, đường biểu diễn quãng đường chạy được của mỗi học sinh là một đồ thị hàm số.

b)

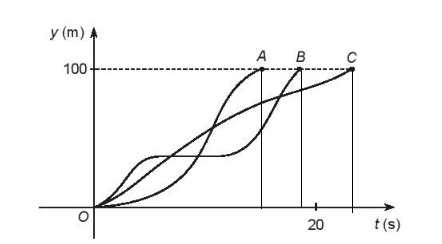
Khi học sinh về đích là khi y = 100 (m), dựa vào chiều dương trục t (s) của đồ thị ta thấy:

Đồ thị A có giá trị t (s) nhỏ nhất ứng với y = 100 (m)

Vậy học sinh A về đích đầu tiên.

Đồ thị của cả ba học sinh đều có giá trị y = 100 (m) nên cả ba học sinh đó đều chạy hết quãng đường thi theo quy định.

Bài 6.6 trang 8 SBT Toán 10 Tập 2: Vẽ đồ thị của các hàm số sau và chỉ ra tập giá trị, các khoảng đồng biến, nghịch biến của chúng.

a) $y=-\frac{1}{2}x+5$;

b) y = 3x²;

c) $y=\left\{\begin{array}{l}{x}^2(x\ge 0)\\ -x-1(x<0)\end{array}\right.$.

Lời giải:

a)

Xét hàm số $y=-\frac{1}{2}x+5$

Ta có:

Khi x = 0 thì $y=-\frac{1}{2}.0+5=5$

Khi x = 10 thì $y=-\frac{1}{2}.10+5=5$

Do đó, đồ thị hàm số là đường thẳng đi qua hai điểm (0; 5) và (10; 0).

Ta có hình vẽ đồ thị hàm số:

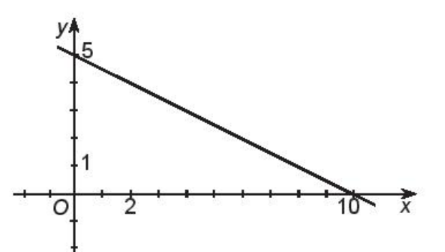
Tập giá trị của hàm số là: T = ℝ.

Đồ thị hàm số luôn đi xuống từ trái sang phải do đó hàm số nghịch biến trên ℝ.

b)

Xét hàm số y = 3x²

Ta có:

Trục đối xứng: x = 0

Đỉnh parabol là: (0; 0)

Khi x = 1 thì y = 3.1² = 3

Khi x = –1 thì y = 3.(–1)² = 3

Do đó, đồ thị hàm số là parabol có đỉnh (0; 0) đi qua hai điểm (1; 3) và (–1; 3)

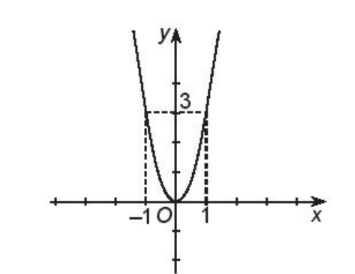
Tập xác định của hàm số là: T = [0; +∞).

Đồ thị hàm số đi xuống từ trái sang phải trên khoảng (–∞; 0) nên hàm số nghịch biến trên khoảng (–∞; 0).

Đồ thị hàm số đi lên từ trái sang phải trên khoảng (0; +∞) nên hàm số đồng biến trên khoảng (0; +∞).

c)

Xét hàm số $y=\left\{\begin{array}{l}{x}^2(x\ge 0)\\ -x-1(x<0)\end{array}\right.$

+) Khi x ≥ 0, ta có:

y = x²

Do đó, đồ thị hàm số là nửa parabol có trục đối xứng x = 0, đỉnh (0; 0), đi qua điểm (1; 1).

+) Khi x < 0, ta có:

y = –x – 1

Do đó, đồ thị hàm số là một phần đường thẳng đi qua điểm (0; –1) và (–1; 0).

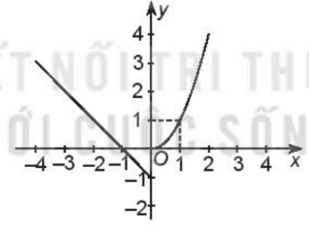
Tập giá trị của hàm số là: T = (–1; +∞)

Đồ thị hàm số đi xuống từ trái sang phải trên khoảng (–∞; 0) nên hàm số nghịch biến trên khoảng (–∞; 0)

Đồ thị hàm số đi lên từ trái sang phải trên khoảng (0; +∞) nên hàm số đồng biến trên khoảng (0; +∞).

Bài 6.7 trang 8 SBT Toán 10 Tập 2: Để đổi nhiệt độ từ thang Celsius sang thang Fahrenheit, ta nhân nhiệt độ theo thang Celsius với $\frac{9}{5}$ sau đó cộng với 32.

a) Viết công thức tính nhiệt độ F ở thang Fahrenheit theo nhiệt độ C ở thang Celsius. Như vậy ta có F là một hàm số của C.

b) Hoàn thành bảng sau:

 c) Vẽ đồ thị của hàm số F = F(C) trên đoạn [–10; 40].

Lời giải:

a)

Để đổi nhiệt độ từ thang Celsius sang thang Fahrenheit, ta nhân nhiệt độ theo thang Celsius với $\frac{9}{5}$ sau đó cộng với 32.

Gọi C là giá trị nhiệt độ ở thang Celsius, F là giá trị nhiệt độ tương ứng ở thang Fahrenheit. Ta có: F = $\frac{9}{5}C+32$

Như vậy, F là một hàm số của C.

b)

Áp dụng công thức hàm số F = $\frac{9}{5}C+32$, ta có bảng:

 c)

Dựa vào bảng phần b, ta có đồ thị hàm số F = F(C) trên đoạn [–10; 40] là đoạn thẳng đi qua 6 điểm (–10; 14), (0; 32), (10; 50), (20; 68), (30; 86), (40; 104).

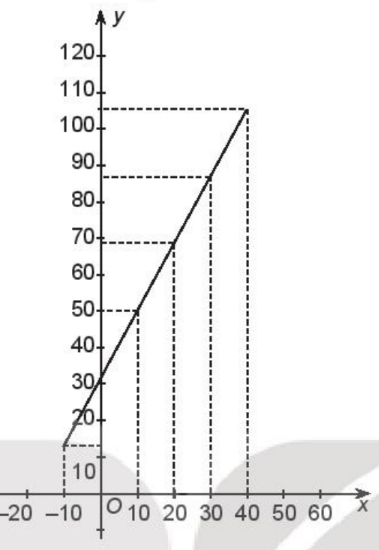
Bài 6.8 trang 8 SBT Toán 10 Tập 2: Giá phòng của một khách sạn là 750 nghìn đồng một ngày cho hai ngày đầu tiên và 500 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách ở tại khách sạn.

a) Viết công thức của hàm số T = T(x).

b) Tính T(2), T(5), T(7) và cho biết ý nghĩa của mỗi giá trị này.

Lời giải:

a)

Với x ≤ 2, ta có: T = T(x) = 750 000x  (đồng).

Với x > 2, ta có:

T = T(x) = 750 000 . 2 + 500 000 . (x – 2)

= 1 500 000 + 500 000x – 1 000 000

= 500 000x + 500 000   (đồng).

Vậy công thức của hàm số $T=T\left(x\right)=$$\left\{\begin{array}{l}750000x(x\le 2)\\ 500000x+500000(x>2)\end{array}\right.$  (đồng).

b)

+) T(2) = 750 000 . 2 = 1 500 000 (đồng)

Nghĩa là số tiền khách phải trả cho 2 ngày mà khách ở tại khách sạn là 1 500 000 đồng

+) T(5) = 500 000 . 5 + 500 000 = 3 000 000

Nghĩa là số tiền khách phải trả cho 5 ngày mà khách ở tại khách sạn là 3 000 000 đồng

+) T(7) = 500 000 . 7 + 500 000 = 4 000 000

Nghĩa là số tiền khách phải trả cho 7 ngày mà khách ở tại khách sạn là 4 000 000 đồng

Bài 6.9 trang 8 SBT Toán 10 Tập 2: Bảng sau đây cho biết giá nước sinh hoạt (chưa tính thuế VAT) của hộ dân cư theo mức sử dụng.

 (Theo hdđt.nshn.com. vn)

a) Hãy tính số tiền phải trả ứng với mỗi lượng nước sử dụng ở bảng sau:

b) Gọi x là lượng nước đã sử dụng (đơn vị m³) và y là số tiền phải trả tương ứng (đơn vị VND). Hãy viết công thức mô tả sự phụ thuộc của y vào x.

Lời giải:

a)

Khi lượng nước sử dụng là 10 m³ ta có số tiền phải trả là:

5 973 . 10 = 59 730 (đồng)

Khi lượng nước sử dụng là 20 m³ ta có số tiền phải trả là:

59 730 + 7 052 . 10 = 130 250 (đồng)

Khi lượng nước sử dụng là 30 m³ ta có số tiền phải trả là:

130 250 + 8 669 . 10 = 216 940 (đồng)

Khi lượng nước sử dụng là 40 m³ ta có số tiền phải trả là:

216 940 + 15 929 . 10 = 376 230 (đồng)

Vậy ta điền được bảng như sau:

 b)

Gọi x là lượng nước đã sử dụng (đơn vị m³) và y là số tiền phải trả tương ứng (đơn vị VND).

Với x ≤ 10 ta có: y = 5 973x

Với 10 < x ≤ 20 ta có: y = 59 730 + 7 052(x – 10)

Với 20 < x  ≤ 30 ta có: y = 130 250 + 8 669(x – 20)

Với x > 30 ta có: y = 216 940 + 15 929(x – 30)

Công thức mô tả sự phụ thuộc của y vào x là:

$y=\left\{\begin{array}{l}y=5973x(x\le 10)\\ y=59730+7052(x-10)(10<x\le 20)\\ y=130250+8669(x-20)(20<x\le 30)\\ y=216940+15929(x-30)(x>30)\end{array}\right.$

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 6 Tập 2

Giải SBT Toán 10 trang 7 Tập 2

Giải SBT Toán 10 trang 9 Tập 2

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 5

Bài 15: Hàm số

Bài 16: Hàm số bậc hai

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai