Với lời giải SBT Toán 10 trang 6 Tập 2 chi tiết trong Bài 15: Hàm số sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 15: Hàm số

Bài 6.1 trang 6 SBT Toán 10 Tập 2: Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là một hàm số của x ?

a) x² + y = 4;

b) 4x + 2y = 6;

c) x + y² = 4;

d) x – y³ = 0.

Lời giải:

 a)

x² + y = 4 ⇔ y = 4 – x²   

Dễ thấy, với một giá trị của x ta chỉ nhận được một giá trị của y tương ứng nên y là hàm số của x.

b)

4x + 2y = 6 ⇔ $y=\frac{6-4x}{2}$⇔ y = 3 – 2x

Dễ thấy, với một giá trị của x ta chỉ nhận được một giá trị của y tương ứng nên y là hàm số của x.

c)

x + y² = 4 ⇔ y² = 4 – x ⇔ y = $\pm \sqrt{4-x}$

Dễ thấy, với một giá trị của x ta có thể nhận được hai giá trị của y tương ứng nên y không là hàm số của x.

Ví dụ: Khi x = 0 thì y = $\pm \sqrt{4-0}=\pm \sqrt{4}=\pm 2$

d)

x – y³ = 0 ⇔ $y=\sqrt[3]{x}$

TXĐ: ℝ

Dễ thấy, với một giá trị của x ta chỉ nhận được một giá trị của y tương ứng nên y là hàm số của x.

Bài 6.2 trang 6 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:

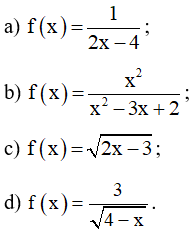
Lời giải:

a)

Điều kiện xác định của hàm số $f\left(x\right)=\frac{1}{2x-4}$ là: 2x – 4 ≠ 0 ⇔ 2x ≠ 4 ⇔ x ≠ 2

Vậy tập xác định của hàm số $f\left(x\right)=\frac{1}{2x-4}$ là: D = ℝ\{2}.

b)

Điều kiện xác định của hàm số $f\left(x\right)=\frac{x^2}{x^2-3x+2}$ là:

x² – 3x + 2 ≠ 0

⇔ (x – 1)(x – 2) ≠ 0

⇔ $\left\{\begin{array}{l}x\ne 1\\ x\ne 2\end{array}\right.$ 

Vậy tập xác định của hàm số $f\left(x\right)=\frac{x^2}{x^2-3x+2}$ là: D = ℝ\{1; 2}.

c)

Điều kiện xác định của hàm số $f\left(x\right)=\sqrt{2x-3}$ là:

2x – 3 ≥ 0

⇔ 2x ≥ 3

⇔ $x\ge \frac{3}{2}$

Vậy tập xác định của hàm số $f\left(x\right)=\sqrt{2x-3}$ là: D = $\left[\frac{3}{2};+\infty \right)$.

d)

Điều kiện xác định của hàm số $f\left(x\right)=\frac{3}{\sqrt{4-x}}$ là:

4 – x > 0

⇔ x < 4

Vậy tập xác định của hàm số $f\left(x\right)=\frac{3}{\sqrt{4-x}}$ là: D = (–∞; 4).

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 7 Tập 2

Giải SBT Toán 10 trang 8 Tập 2

Giải SBT Toán 10 trang 9 Tập 2

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 5

Bài 15: Hàm số

Bài 16: Hàm số bậc hai

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai