Với lời giải SBT Toán 10 trang 81 Tập 1 chi tiết trong Bài 14: Các số đặc trưng đo độ phân tán sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 14: Các số đặc trưng đo độ phân tán
Bài 5.16 trang 81 SBT Toán 10 Tập 1:
Trong các dãy số liệu sau, dãy nào có độ lệch chuẩn lớn nhất?
(a) 98 99 100 101 102.
(b) 2 4 6 8 10.
(c) 2 10.
Lời giải:
– Đối với dãy (a) ta có:
• Số trung bình là:
• Phương sai là:
![]()
• Độ lệch chuẩn là:
– Đối với dãy (b) ta có:
• Số trung bình là:
• Phương sai là:
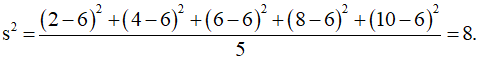
• Độ lệch chuẩn là:
– Đối với dãy (c) ta có:
• Số trung bình là:
• Phương sai là:
• Độ lệch chuẩn là:
Vì 1,41 < 2,83 < 4 nên độ lệch chuẩn của dãy (c) lớn nhất.
Vậy độ lệch chuẩn của dãy số liệu (c) là lớn nhất.
Bài 5.17 trang 81 SBT Toán 10 Tập 1:
Mẫu số liệu sau là chiều cao (đơn vị: cm) của các bạn trong tổ của Lan:
165 168 157 162 165 165 179 148 170 167.
a) Tính khoảng tứ phân vị của mẫu số liệu trên.
b) Khoảng tứ phân vị có bị ảnh hưởng bởi chiều cao của bạn cao nhất, bạn thấp nhất không?
Lời giải:
a) Sắp xếp dãy số liệu theo thứ tự không giảm ta được:
148 157 162 165 165 165 167 168 170 179.
• Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa (số liệu thứ 5 và thứ 6) của mẫu số liệu đã sắp xếp.
Do đó Q2 =
• Nửa dữ liệu bên trái Q2 là: 148; 157; 162; 165; 165.
Dãy này gồm 5 số liệu, n = 5 là số lẻ nên trung vị là giá trị chính giữa (số liệu thứ 3 của nửa dữ liệu bên trái Q2) nên Q1 = 162.
• Nửa dữ liệu bên phải Q2 là: 165; 167; 168; 170; 179.
Dãy này gồm 5 số liệu, n = 5 là số lẻ nên trung vị là giá trị chính giữa (số liệu thứ 3 của nửa dữ liệu bên phải Q2) nên Q3 = 168.
Khi đó khoảng tứ phân vị của mẫu số liệu đã cho là:
DQ = Q3 – Q1 = 168 – 162 = 6.
Vậy khoảng tứ phân vị của mẫu số liệu đã cho là 6 cm.
b) Khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp nên đo độ phân tán của 50% dữ liệu này.
Do đó khoảng tứ phân vị không bị ảnh hưởng bởi giá trị nhỏ nhất, giá trị lớn nhất.
Vậy khoảng tứ phân vị không bị ảnh hưởng bởi chiều cao của bạn cao nhất và bạn thấp nhất.
Bài 5.18 trang 81 SBT Toán 10 Tập 1:
Bình dùng đồng hồ đo thời gian để một vật rơi tự do (đơn vị: giây) từ vị trí A đến vị trí B trong 10 lần cho kết quả như sau:
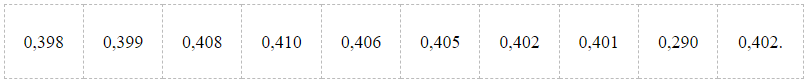
Bình nghĩ là giá trị 0,290 ở lần đo thứ 9 không chính xác. Hãy kiểm tra nghi ngờ của Bình.
Lời giải:
Sắp xếp dãy số liệu theo thứ tự không giảm ta được:
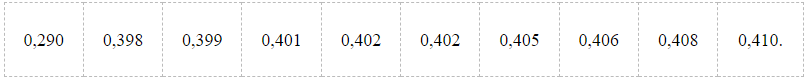
• Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa (số liệu thứ 5 và thứ 6) của mẫu số liệu đã sắp xếp.
Do đó Q2 =
• Nửa dữ liệu bên trái Q2 là: 0,290; 0,398; 0,399; 0,401; 0,402.
Dãy này gồm 5 số liệu, n = 5 là số lẻ nên trung vị là giá trị chính giữa (số liệu thứ 3 của nửa dữ liệu bên trái Q2) nên Q1 = 0,399.
• Nửa dữ liệu bên phải Q2 là: 0,402; 0,405; 0,406; 0,408; 0,410.
Dãy này gồm 5 số liệu, n = 5 là số lẻ nên trung vị là giá trị chính giữa (số liệu thứ 3 của nửa dữ liệu bên phải Q2) nên Q3 = 0,406.
Khi đó khoảng tứ phân vị của mẫu số liệu đã cho là:
DQ = Q3 – Q1 = 0,406 – 0,399 = 0,007.
Ta có: Q1 – 1,5.DQ = 0,399 – 1,5.0,007 = 0,3885.
Vì 0,290 < 0,3885 nên đây là giá trị bất thường.
Vậy giá trị 0,290 ở lần đo thứ 9 không chính xác.
Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Giải SBT Toán 10 trang 80 Tập 1
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 13: Các số đặc trưng đo xu thế trung tâm
Bài 14: Các số đặc trưng đo độ phân tán