Với giải bài 89 trang 111 Toán lớp 8 chi tiết trong Ôn tập chương 1 Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Ôn tập chương 1 Hình học
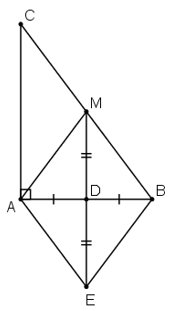
Bài 89 trang 111 Toán 8 Tập 1:Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm dối xứng với M qua D.
a) Chứng minh rằng điểm E đối xứng với điểm M qua AB.
b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c) Cho BC = 4cm, tính chu vì tứ giác AEBM.
d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông?
Lời giải:
a) Xét , ta có:
MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC,
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD (cmt).
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
(vì M là trung điểm của BC)
Chu vi hình thoi AEBM bằng
4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông ⇔ AB = EM
Mà EM = AC
⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
- Cách 2:
Hình thoi AEBM là hình vuông
⇔ AM ⊥ BM
⇔ ΔABC có trung tuyến AM là đường cao
⇔ ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.
Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:
Câu hỏi 1 trang 110 Toán 8 Tập 1: Phát biểu định nghĩa tứ giác...
Câu hỏi 2 trang 110 Toán 8 Tập 1:Phát biểu định nghĩa hình thang, hình thang cân...
Câu hỏi 3 trang 110 Toán 8 Tập 1:Phát biểu các tính chất của hình thang cân...
Bài 90 trang 111 Toán 8 Tập 1:Đố. Tìm trục đối xứng và tâm đối xứng của:...