Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 8: Ôn tập chương 1 Hình học chọn lọc, có đáp án. Tài liệu gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 8. Hi vọng với bộ câu hỏi trắc nghiệm Ôn tập chương 1 Hình học có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi môn Toán 8.
Giới thiệu về tài liệu:
- Số câu hỏi trắc nghiệm: 30 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Ôn tập chương 1 Hình học có đáp án - Toán lớp 8:

Trắc nghiệm Toán 8
Ôn tập chương 1 Hình học
Bài 1: Cho tứ giác ABCD, có 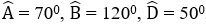
A. 1000
B. 1050
C. 1200
D. 1150
Lời giải
Xét tứ giác ABCD ta có:
Đáp án cần chọn là: C
Bài 2: Hình thang ABCD (AB // CD) có số đo góc D bằng 700, số đo góc A là:
A. 1300
B. 900
C. 1100
D. 1200
Lời giải
Đáp án cần chọn là: C
Bài 3: Một tam giác đều có độ dài cạnh bằng 14cm. Độ dài một đường trung bình của tam giác đó là:
A. 34cm
B. 7cm
C. 6,5cm
D. 21cm
Lời giải
Độ dài một đường trung bình của tam giác là: 14 : 2 = 7cm
Đáp án cần chọn là: B
Bài 4: Một hình thang cân có cạnh bên là 2,5cm; đường trung bình là 3cm. Chu vi của hình thang là:
A. 8cm
B. 12cm
C. 11,5cm
D. 11cm
Lời giải
Tổng độ dài hai đáy là: 3.2 = 6 (cm)
Chu vi hình thang là: 2,5.2 + 6 = 11 (cm)
Đáp án cần chọn là: D
Bài 5: Độ dài một cạnh hình vuông bằng 5cm. Thì độ dài đường chéo hình vuông đó sẽ là:
A. 25cm
B. 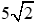
C. 10cm
D. 5cm
Lời giải
Cho hình vuông ABCD có cạnh bằng 5cm.
Xét tam giác ABD vuông tại A, theo định lý Pytago ta có:
BD2 + AB2 + AD2 = 52 + 52 = 50
Đáp án cần chọn là: B
Bài 6: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Hai đường chéo AC và BD phải thỏa mãn điều kiện gì dể M, N, P, Q là bốn đỉnh của hình vuông.
A. BD = AC
B. BD ⊥ AC
C. BD tạo với AC góc 600
D. BD = AC; BD ⊥ AC
Lời giải
Xét tam giác ABD có:
M là trung điểm của AB (gt)
Q là trung điểm của AD (gt)
⇒ QM là đường trung bình của tam giác ABD. (định lý)
Do đó QM // BD và QM = ½BD (1)
Tương tự ta cũng có NP là đường trung bình của tam giác BCD.
Từ (1) và (2) suy ra MNPQ là hình bình hành (dấu hiệu nhận biết)
Tương tự ta cũng có MN là đường trung bình của tam giác BAC nên MN // AC và MN = ½AC
Để hình bình hành MNPQ là hình vuông
+ Để MN ⊥ NP ⇔ AC ⊥ BD (vì MN // AC, NP // BD)
+ Để MN = NP ⇔ AC = BD (vì MN = ½AC, NP = ½BD)
Vậy điều kiện cần để MNPQ là hình vuông là BD = AC; AC ⊥ BD
Đáp án cần chọn là: D
Bài 7: Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, CA. Gọi M, N, P, Q theo thứ tự là trung điểm của AD, AF, EF, ED.
ΔABC có điều kiện gì thì MNPQ là hình chữ nhật?
A. ΔABC cân tại A
B. ΔABC cân tại B
C. ΔABC cân tại C
D. ΔABC vuông tại A
Lời giải
Xét ΔADE có: AM = MD; DQ = EQ nên MQ là đường trung bình của ΔADE
⇒ MQ // AE, MQ = 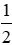
Xét ΔAEF có: AN = NF; FP = PE (giả thiết) nên NP là đường trung bình của ΔAEF.
⇒ NP // AE , NP = 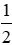
Suy ra MQ // NP (cùng // AE) và MQ = NP (= 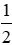
Tứ giác MNPQ có: MQ // NP và MQ = NP nên là hình bình hành (dấu hiệu nhận biết).
Để MNPQ là hình chữ nhật thì MN ⊥ PQ (1)
Ta có: NP // AE (chứng minh trên) (2)
Ta lại có: AM = MD, AN = NF (gt) ⇒ MN // DF
Mặt khác: AD = DB, AF = FC (gt) ⇒ DF // BC
Vậy MN // BC (3)
Từ (1), (2), (3) suy ra: AE ⊥ BC
Mà BE = EC (gt)
Do đó ΔABC cân tại A (do AE vừa là đường cao, vừa là đường trung tuyến)
Đáp án cần chọn là: A
Bài 8: Cho tam giác ABC (Â < 900). Về phía ngoài của tam giác ABC dựng các hình vuông ABDE, ACFG. Gọi M là trung điểm của đoạn thẳng DF. Chọn câu đúng.
A. Tam giác MBC vuông cân tại M
B. Tam giác MBC cân tại B
C. Tam giác MBC cân tại C
D. Tam giác MBC đều
Lời giải
Trên nửa mặt phẳng bờ BC có chứa A dựng tam giác BHC vuông cân đỉnh B
Xét tam giác BHD và tam giác BCA có:
DB = BA (vì ADBE là hình vuông)
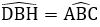
BH = BC (vì tam giác BHC vuông cân đỉnh B)
Do đó: ΔBHD = ΔBCA (c.g.c), suy ra DH = AC,
AC cắt HD tại K, cắt BH tại I.
Xét tam giác IHK và tam giác ICB có:
Mặt khác KC ⊥ CF, do đó DH // CF
Ta có DH = CF (=AC) và DH // CF nên DHCF là hình bình hành
Mà M là trung điểm của DF nên M là trung điểm của HC, suy ra tam giác MBC vuông cân đỉnh M
Đáp án cần chọn là: A
Bài 9: Cho hình vuông ABCD, E là một điểm trên cạnh CD. Tia phân giác của góc BAE cắt BC tại M. Chọn câu đúng.
A. AM = ME
B. AM < ME
C. AM ≤ 2ME
D. AM > 2ME
Lời giải
Vẽ EF ⊥ AM (F Є AB), EG ⊥ AB (G Є AB).
Tứ giác AGED là hình chữ nhật (vì 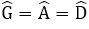
Lại thấy
Xét ΔGEF và ΔBAM có:
Do đó ΔGEF = ΔBAM (g.c.g) suy ra EF = AM
Tam giác AEF có AM là đường phân giác và là đường cao nên tam giác AEF cân đỉnh A
Ta có AM là đường trung trực của EF, nên ME – MF
Xét ba điểm M, E, F ta có: EF ≤ ME + MF ⇔ EF ≤ 2ME.
Do đó AM ≤ 2ME
Đáp án cần chọn là: C
Bài 10: Hình thoi có độ dài hai đường chéo lần lượt bằng 12cm và 16cm. Độ dài cạnh hình thoi đó là:
A. 14cm
B. 28 cm
C. 100 cm
D. 10 cm
Lời giải
Giả sử hình thoi ABCD có hai đường chéo AC = 16cm, BD = 12cm cắt nhau tại O.
Theo tính chất hình thoi ta có AC vuông góc với BD, O là trung điểm của AC, BD
Do đó: OA = 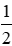
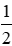
Áp dụng định lý Pytago cho tam giác ABO vuông tại O ta có:
AB2 = OA2 + OB2 = 62 + 82 = 100 ⇒ AB = 10(cm)
Vậy độ dài cạnh hình thoi là 10cm
Đáp án cần chọn là: D
Bài 11: Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điêm của MN với BD, AC. Cho biết AB = 6cm, CD = 14cm. Tính độ dài MI, IK.
A. MI = 4cm, IK = 7cm
B. MI = 4cm, IK = 3cm
C. MI = 3cm, IK = 7cm
D. MI = 3cm, IK = 4cm
Lời giải
- Hình thang ABCD có 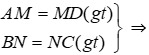
⇒ MN // AB // CD (tính chất)
- Tam giác ABD có: 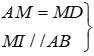
⇒ MI là đường tủng bình của ΔADB
- Tương tự tam giác ACD có:
AM = MD, MK // DC nên AK = KC, hay MK là đường trung bình của tam giác ACD, ta có:
⇒ IK = MK – MI = 7 – 3 = 4(cm)
Vậy MI = 3cm; IK = 4cm
Đáp án cần chọn là: D
Bài 12: Cho hình bình hành ABCD có DC = 2BC. Gọi E, F là trung điểm của AB, DC. Gọi AF cắt DE tại I, BF cắt CE tại K.
1. Chọn câu đúng nhất.
A. Tứ giác DEBF là hình bình hành
B. Tứ giác AEFD là hình thoi
C. Tứ giác EBCF là hình vuông
D. Cả A, B đều đúng
Lời giải
Xét hình bình hành ABCD có E, F lần lượt là trung điểm của AB, CD, DC = 2BC nên AE = EB = BC = CF = DF = AD; AB // CD, AD // BC
Xét tứ giác DEBF có 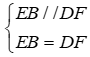
Xét tứ giác AEFD có AE = DF; AE // DF nên AEDF là hình bình hành, lại có AE = AD nên hình bình hành AEFD là hình thoi.
Tương tự ta cũng có EBCF là hình thoi. Nhận thấy chưa đủ điều kiện để EBCF là hình vuông.
Nên A, B đúng, C sai.
Đáp án cần chọn là: D
2. Tứ giác EIFK là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Cả A, B, C đều sai
Lời giải
Theo câu trước ta có tứ giác BEDF là hình bình hành nên
ED = BF, ED // BF ⇒ EI // FK (1)
Theo câu trước ta có tứ giác AEDF và BEFC là hình thoi nên I, K lần lượt là trung điểm của DE và BF.
Suy ra 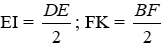
Từ (1) và (2) suy ra tứ giác EIFK là hình bình hành.
Mà AEDF là hình thoi nên AF ⊥ DE (tính chất hình thoi) ⇒
Hình bình hành EIFK có một góc vuông 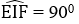
Đáp án cần chọn là: A
Bài 13: Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I.
1. Tứ giác AMCK là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Cả A, B, C đều sai
Lời giải
ΔABC cân tại A có AM là trung tuyến nên AM đồng thời là đường cao
Xét tứ giác AMCK có AC cắt MK tại I, mà AI = IC, MI = IK (gt)
⇒ Tứ giác AMCk là hình bình hành (dấu hiệu nhận biết) (2)
Từ (1) và (2) ⇒ AMCK là hình chữ nhật (dấu hiệu nhận biết)
Đáp án cần chọn là: A
2. Tứ giác AKMB là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Hình bình hành
Lời giải
Tứ giác AMCK là hình chữ nhật (câu trên) ⇒ AK // CM ⇒ AK // BM (3)
Mà AK = MC (AMCK là hình chữ nhật) và MC = MB (gt)
⇒ AK = BM (4)
Từ (3) và (4) ⇒ Tứ giác AKMB là hình bình hành (dấu hiệu nhận biết)
Đáp án cần chọn là: D
Bài 14: Cho hình bình hành ABCD có BC = 2AB và Â = 600. Gọi E, F theo thứ tự là trung điểm của BC và AD. Gọi I là điểm đối xứng với A qua B.
1. Tứ giác BICD là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Hình bình hành
Lời giải
Do AB // CD (giả thiết) nên BI // CD
Mặt khác BI = AB (gt) ; AB = CD (gt) ⇒ BI = CD
Vậy BICD là hình bình hành (1)
Theo giả thiết ta có
BI = AB = AF = FD ⇒ AI = AD mà 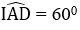
Xét tam giác ADI đều có BD là trung tuyến đồng thời là đường cao.
Từ (1) và (2) suy ra BICD là hình chữ nhật (dấu hiệu nhận biết)
Đáp án cần chọn là: A
3. Số đo góc AED là:
A. 450
B. 600
C. 900
D. 1000
Lời giải
Theo câu trước ta có BICD là hình chữ nhật lại có E là trung điểm của BC (gt) nên E cũng là trung điểm của ID.
Mà tam giác ADI đều (theo câu trước) có AE là đường trung tuyến nên AE cũng là đường cao, suy ra AE ⊥ BD ⇒
Đáp án cần chọn là: C
Bài 15: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Hai đường chéo AC và BD phải thỏa mãn điều kiện gì dể M, N, P, Q là bốn đỉnh của hình vuông.
A. BD = AC
B. BD ⊥ AC
C. BD tạo với AC góc 600
D. BD = AC; BD ⊥ AC
Lời giải
Xét tam giác ABD có:
M là trung điểm của AB (gt)
Q là trung điểm của AD (gt)
⇒ QM là đường trung bình của tam giác ABD. (định lý)
Do đó QM // BD và QM = ½BD (1)
Tương tự ta cũng có NP là đường trung bình của tam giác BCD.
Từ (1) và (2) suy ra MNPQ là hình bình hành (dấu hiệu nhận biết)
Tương tự ta cũng có MN là đường trung bình của tam giác BAC nên MN // AC và MN = ½AC
Để hình bình hành MNPQ là hình vuông
+ Để MN ⊥ NP ⇔ AC ⊥ BD (vì MN // AC, NP // BD)
+ Để MN = NP ⇔ AC = BD (vì MN = ½AC, NP = ½BD)
Vậy điều kiện cần để MNPQ là hình vuông là BD = AC; AC ⊥ BD
Đáp án cần chọn là: D
Bài 16: Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, CA. Gọi M, N, P, Q theo thứ tự là trung điểm của AD, AF, EF, ED.
ΔABC có điều kiện gì thì MNPQ là hình chữ nhật?
A. ΔABC cân tại A
B. ΔABC cân tại B
C. ΔABC cân tại C
D. ΔABC vuông tại A
Lời giải
Xét ΔADE có: AM = MD; DQ = EQ nên MQ là đường trung bình của ΔADE
⇒ MQ // AE, MQ = 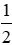
Xét ΔAEF có: AN = NF; FP = PE (giả thiết) nên NP là đường trung bình của ΔAEF.
⇒ NP // AE , NP = 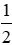
Suy ra MQ // NP (cùng // AE) và MQ = NP (= 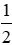
Tứ giác MNPQ có: MQ // NP và MQ = NP nên là hình bình hành (dấu hiệu nhận biết).
Để MNPQ là hình chữ nhật thì MN ⊥ PQ (1)
Ta có: NP // AE (chứng minh trên) (2)
Ta lại có: AM = MD, AN = NF (gt) ⇒ MN // DF
Mặt khác: AD = DB, AF = FC (gt) ⇒ DF // BC
Vậy MN // BC (3)
Từ (1), (2), (3) suy ra: AE ⊥ BC
Mà BE = EC (gt)
Do đó ΔABC cân tại A (do AE vừa là đường cao, vừa là đường trung tuyến)
Đáp án cần chọn là: A
Bài 17: Cho tam giác ABC (Â < 900). Về phía ngoài của tam giác ABC dựng các hình vuông ABDE, ACFG. Gọi M là trung điểm của đoạn thẳng DF. Chọn câu đúng.
A. Tam giác MBC vuông cân tại M
B. Tam giác MBC cân tại B
C. Tam giác MBC cân tại C
D. Tam giác MBC đều
Lời giải
Trên nửa mặt phẳng bờ BC có chứa A dựng tam giác BHC vuông cân đỉnh B
Xét tam giác BHD và tam giác BCA có:
DB = BA (vì ADBE là hình vuông)
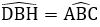
BH = BC (vì tam giác BHC vuông cân đỉnh B)
Do đó: ΔBHD = ΔBCA (c.g.c), suy ra DH = AC,
AC cắt HD tại K, cắt BH tại I.
Xét tam giác IHK và tam giác ICB có:
Mặt khác KC ⊥ CF, do đó DH // CF
Ta có DH = CF (=AC) và DH // CF nên DHCF là hình bình hành
Mà M là trung điểm của DF nên M là trung điểm của HC, suy ra tam giác MBC vuông cân đỉnh M
Đáp án cần chọn là: A
Bài 18: Cho hình vuông ABCD, E là một điểm trên cạnh CD. Tia phân giác của góc BAE cắt BC tại M. Chọn câu đúng.
A. AM = ME
B. AM < ME
C. AM ≤ 2ME
D. AM > 2ME
Lời giải
Vẽ EF ⊥ AM (F Є AB), EG ⊥ AB (G Є AB).
Tứ giác AGED là hình chữ nhật (vì 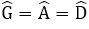
Lại thấy
Xét ΔGEF và ΔBAM có:
Do đó ΔGEF = ΔBAM (g.c.g) suy ra EF = AM
Tam giác AEF có AM là đường phân giác và là đường cao nên tam giác AEF cân đỉnh A
Ta có AM là đường trung trực của EF, nên ME – MF
Xét ba điểm M, E, F ta có: EF ≤ ME + MF ⇔ EF ≤ 2ME.
Do đó AM ≤ 2ME
Đáp án cần chọn là: C
Bài giảng Toán 8 Ôn tập chương 1 Hình học