Với giải bài 77 trang 106 Toán lớp 8 chi tiết trong Bài 11: Hình thoi giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 11: Hình thoi

Bài 77 trang 106 Toán 8 Tập 1: Chứng minh rằng:

a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.

b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.

Lời giải:

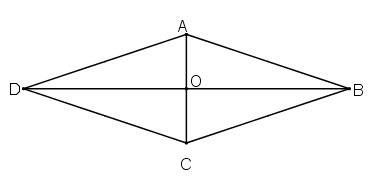
a) Gọi O là giao điểm của hai đường chéo của hình thoi ABCD

Vì ABCD là hình thoi nên ABCD là hình bình hành

Mà tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.

Suy ra O là tâm đối xứng của hình thoi ABCD.

b)

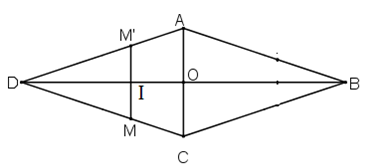
Xét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.

* Ta chứng minh: đường chéo BD là trục đối xứng của hình

Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.

Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi

+ Gọi I là giao điểm của MM’ và BD.

Xét tam giác DIM và DIM’ có:

$\widehat{DIM}=\widehat{DIM\text{'}}=90°$

DI chung

IM= IM’ ( do M và M’ đối xứng với nhau qua BD)

$\Rightarrow$∆DIM = ∆DIM’ ( c.g.c)

$\Rightarrow \widehat{IDM}=\widehat{IDM\text{'}}$ và DM = DM’

Lại có: ABCD là hình thoi nên $\widehat{IDA}=\widehat{IDC}$ (DB là phân giác $\widehat{ADC}$) hay $\widehat{IDA}=\widehat{IDM}$

Mà $\widehat{IDM}=\widehat{IDM\text{'}}$

$\Rightarrow \widehat{IDA}=\widehat{IDM\text{'}}$

Suy ra điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi

Do đó BD là trục đối xứng của hình thoi.

Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi.

Vậy hai đường chéo AC, BD là hai trục đối xứng của hình thoi.

Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

Câu hỏi 1 trang 104 Toán 8 Tập 1: Chứng minh rằng tứ giác ABCD trên Hình 100 cũng là một hình bình hành...

Câu hỏi 2 trang 104 Toán 8 Tập 1: Cho hình thoi ABCD, hai đường chéo cắt nhau tại O (h.101)...

Câu hỏi 3 trang 105 Toán 8 Tập 1: Hãy chứng minh dấu hiệu nhận biết 3...

Bài 73 trang 105 Toán 8 Tập 1: Tìm các hình thoi trên hình 102...

Bài 74 trang 106 Toán 8 Tập 1: Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:...

Bài 75 trang 106 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi...

Bài 76 trang 106 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật...

Bài 78 trang 106 Toán 8 Tập 1: Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bằng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng?...