Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài tập ôn cuối năm hay, chi tiết giúp học sinh dễ dàng làm bài tập Bài tập ôn cuối năm lớp 8.

Giải bài tập Toán lớp 8 Bài tập ôn cuối năm

Phần đại số

Bài 1 trang 130 SGK Toán lớp 8 tập 2: Phân tích các đa thức sau thành nhân tử:

a) a² – b² – 4a + 4;

b) x² + 2x – 3;

c) 4x²y² – (x² + y²)²;

d) 2a³ – 54b³.

Lời giải:

a) a² – b² – 4a + 4

= a² – 4a + 4 – b²

= (a – 2)² – b²

= (a – 2 + b)(a – 2 – b)

= (a + b – 2)(a – b – 2)

b) x² + 2x – 3

= x² + 2x + 1 – 4

= (x + 1)² – 2²

= (x + 1 + 2)(x + 1 – 2)

= (x + 3)(x – 1)

c) 4x²y² – (x² + y²)²

= (2xy)² – (x² + y²)²

= (2xy + x² + y²)(2xy - x² - y²)

= - (x² + 2xy + y²).(x² - 2xy + y²)

= -(x + y)² .(x - y)²

d) 2a³ – 54b³

= 2(a³ – 27b³)

= 2[a³ – (3b)³]

= 2(a – 3b)(a² + 3ab + 9b²)

Bài 2 trang 130 SGK Toán lớp 8 tập 2: a) Thực hiện phép chia:

(2x⁴ – 4x³ + 5x² + 2x – 3):(2x² - 1)

b) Chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của x.

Lời giải:

a) Thực hiện phép chia

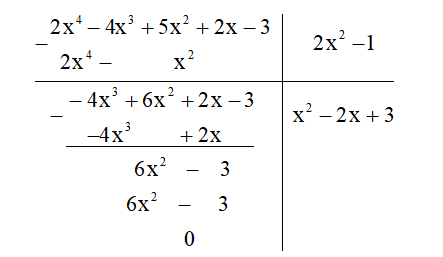
Vậy (2x⁴ – 4x³ + 5x² + 2x – 3) : (2x² – 1) = x² – 2x + 3.

b) Ta có:

x² – 2x + 3

= x² – 2x + 1 + 2

= (x – 1)² + 2

Vì (x – 1)² ≥ 0 với ∀ x

⇒ x² – 2x + 3 = (x – 1)² + 2 ≥ 2 > 0 với ∀ x

Vậy thương tìm được luôn luôn dương với mọi giá trị của x.

Bài 3 trang 130 SGK Toán lớp 8 tập 2: Chứng minh rằng hiệu các bình phương của hai số lẻ bất kì thì chia hết cho 8.

Lời giải:

Gọi hai số lẻ bất kì là 2a + 1 và 2b + 1 (a, b ∈ Z).

Hiệu bình phương của hai số lẻ đó bằng:

(2a + 1)² – (2b + 1)²

= (4a² + 4a + 1) – (4b² + 4b + 1)

= (4a² + 4a) – (4b² + 4b)

= 4a(a + 1) – 4b(b + 1)

Tích của hai số tự nhiên liên tiếp luôn chia hết cho 2

⇒ a.(a + 1) ⋮ 2 và b.(b + 1) ⋮ 2.

⇒ 4a(a + 1) ⋮ 8 và 4b(b + 1) ⋮ 8

⇒ 4a(a + 1) – 4b(b + 1) ⋮ 8.

Vậy (2a + 1)² – (2b + 1)² chia hết cho 8 (đpcm).

Bài 4 trang 130 SGK Toán lớp 8 tập 2: Rút gọn rồi tính giá trị của biểu thức sau tại $x=\frac{-1}{3}$.

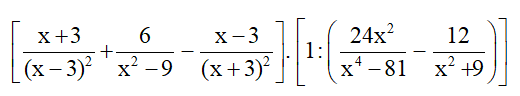
Lời giải:

Điều kiện xác định: $x\pm 3$

* Rút gọn biểu thức:

+ Ngoặc vuông thứ nhất:

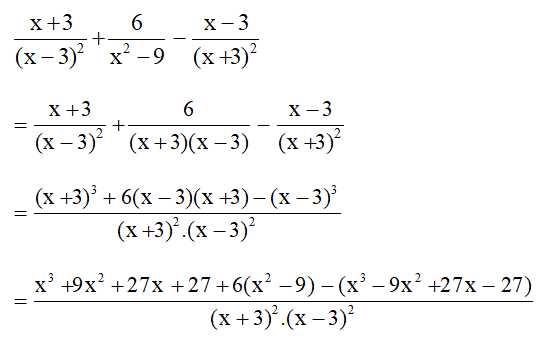
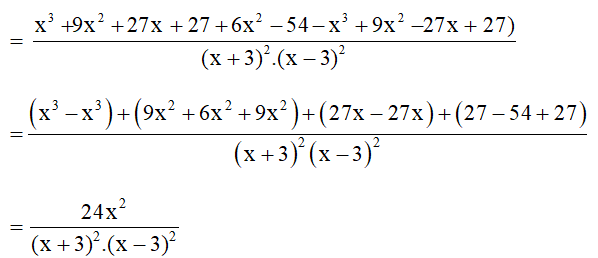
+ Ngoặc vuông thứ hai:

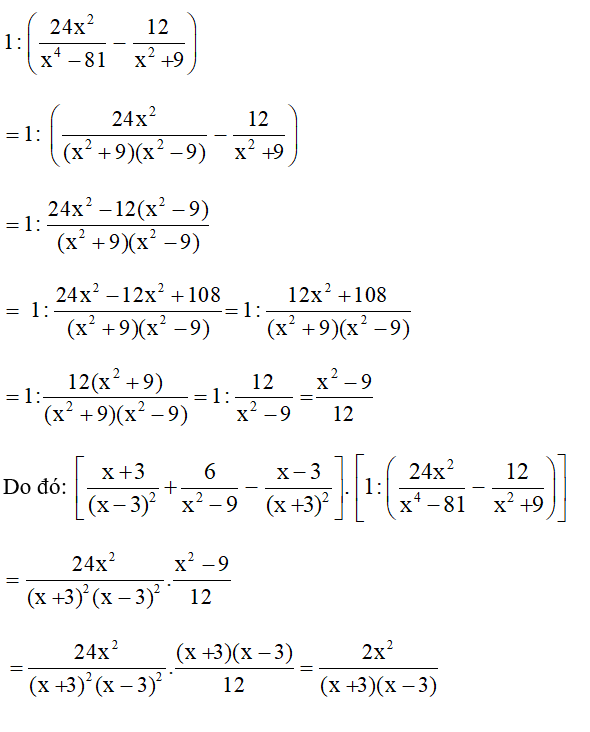
* Tại $x=\frac{-1}{3}$  (thỏa mãn điều kiện), giá trị biểu thức là $\frac{2.{\left(\frac{-1}{3}\right)}^2}{\left(\frac{-1}{3}+3\right).\left(\frac{-1}{3}-3\right)}=\frac{-1}{40}$

Bài 5 trang 130 SGK Toán lớp 8 tập 2: Chứng minh rằng:

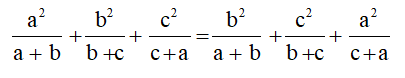
Lời giải:

Giả sử:

$\frac{a^2}{a+\text{\hspace{0.17em}\hspace{0.17em}}b}+\text{\hspace{0.17em}}\frac{b^2}{b+\text{}c}+\frac{c^2}{c\text{\hspace{0.17em}}+a}=\frac{b^2}{a+\text{\hspace{0.17em}\hspace{0.17em}}b}+\text{\hspace{0.17em}}\frac{c^2}{b+\text{}c}+\frac{a^2}{c\text{\hspace{0.17em}}+a}$

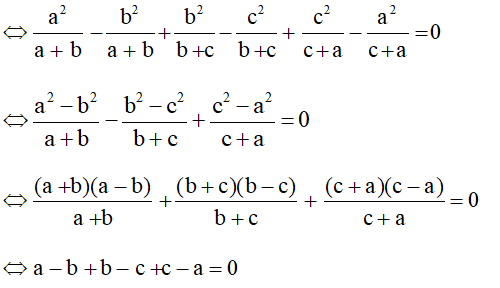
Hay 0 = 0 luôn đúng (đpcm).

Vậy $\frac{a^2}{a+\text{\hspace{0.17em}\hspace{0.17em}}b}+\text{\hspace{0.17em}}\frac{b^2}{b+\text{}c}+\frac{c^2}{c\text{\hspace{0.17em}}+a}=\frac{b^2}{a+\text{\hspace{0.17em}\hspace{0.17em}}b}+\text{\hspace{0.17em}}\frac{c^2}{b+\text{}c}+\frac{a^2}{c\text{\hspace{0.17em}}+a}$

Bài 6 trang 130 SGK Toán lớp 8 tập 2: Tìm các giá trị nguyên của x để phân thức M có giá trị một số nguyên:

$M=\frac{10x^2-7x-5}{2x-3}$

Lời giải:

Điều kiện: $x\ne \frac{3}{2}$

Ta có: 

$$\begin{gathered} M=\frac{10x^2-7x-5}{2x-3} \\ =5x\text{}+4+\frac{7}{2x-3} \end{gathered}$$

(thực hiện phép chia đa thức cho đa thức).

Để M nguyên khi $5x+4+\frac{7}{2x-3}\in Z$

Vì x nguyên nên 5x +4 nguyên

Suy ra: $\frac{7}{2x-3}\in Z$

Suy ra: 2x – 3  $\in \text{\hspace{0.17em}\hspace{0.17em}}U\left(7\right)=\left\{\pm 1;\pm 7\right\}$.

Ta có bảng sau:

2x - 3	-1	1	-7	7
2x	2	4	-4	10
x	1	2	-2	5

Vậy với x ∈ {-2; 1; 2; 5} thì giá trị biểu thức M là một số nguyên.

Bài 7 trang 130 SGK Toán lớp 8 tập 2: Giải các phương trình:

a) $\frac{4x+3}{5}-\frac{6x-2}{7}=\frac{5x+4}{3}+3$;

b) $\frac{3(2x-1)}{4}-\frac{3x+1}{10}+1=\frac{2(3x+\text{}2)}{5}$;

c) $\frac{x+2}{3}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{3(2x-1)}{4}-\frac{5x-3}{6}=x+\frac{5}{12}$.

Lời giải:

a)

$$\begin{gathered} \frac{4x+3}{5}-\frac{6x-2}{7}=\frac{5x+4}{3}+3 \\ \iff \frac{21(\text{}4x+3)-15(6x-2)}{105}=\frac{35(5x+4)+3.105}{105} \end{gathered}$$

⇔ 21(4x + 3) – 15(6x – 2) = 35(5x + 4) + 105.3

⇔ 84x + 63 – 90x + 30 = 175x + 140 + 315

⇔ 84x – 90x – 175x = 140 + 315 – 63 – 30

⇔ -181x = 362

⇔ x = -2.

Vậy phương trình có nghiệm x = -2.

b) $\frac{3(2x-1)}{4}-\frac{3x+1}{10}+1=\frac{2(3x+\text{}2)}{5}$

$\iff \frac{15(2x-1)-2(3x+\text{}1)+20}{20}=\frac{8(3x+2)}{20}$

⇔ 15(2x – 1) – 2(3x + 1) + 20 = 8(3x + 2)

⇔ 30x – 15 – 6x – 2 + 20 = 24x + 16

⇔ 30x – 6x – 24x = 16 – 20 + 15 + 2

⇔ 0x = 13 vô lí.

Vậy phương trình vô nghiệm.

c) $\frac{x+2}{3}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{3(2x-1)}{4}-\frac{5x-3}{6}=x+\frac{5}{12}$.

$\iff \frac{4(x+2)+\text{}9(2x-1)-2(5x-3)}{12}=\frac{12x+5}{12}$

⇔ 4(x + 2) + 9(2x – 1) – 2(5x – 3) = 12x + 5

⇔ 4x + 8 + 18x – 9 – 10x + 6 = 12x + 5

⇔ 4x + 18x – 10x – 12x = 5 – 8 + 9 – 6

⇔ 0x = 0 luôn đúng.

Vậy phương trình nghiệm đúng với mọi x.

Bài 8 trang 130 SGK Toán lớp 8 tập 2: Giải các phương trình:

a) |2x – 3| = 4 ;    

b) |3x – 1| - x = 2.

Lời giải:

a)

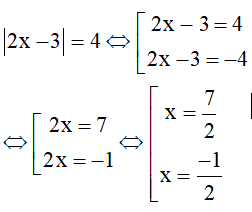
Vậy tập nghiệm của phương trình đã cho là $S=\left\{\frac{-1}{2};\frac{7}{2}\right\}$.

b) |3x – 1| - x = 2   (1)

+ Trường hợp 1: Nếu $3x-1\ge 0\iff x\ge \frac{1}{3}$

Khi đó: |3x – 1| = 3x – 1.

(1) trở thành: 3x – 1 – x = 2 ⇔ 2x = 3 ⇔  $x=\frac{3}{2}$ (thỏa mãn).

+ Trường hợp 2: Nếu 3x – 1 < 0 hay $x<\frac{1}{3}$

Khi đó |3x – 1| = -(3x – 1) = 1 – 3x.

(1) trở thành: 1 – 3x – x = 2 ⇔ 1 – 4x = 2 ⇔ 4x = -1 ⇔ $x=\frac{-1}{4}$  (thỏa mãn).

Vậy phương trình (1) có tập nghiệm $S=\left\{\frac{-1}{4};\frac{3}{2}\right\}$ .

Bài 9 trang 130-131 SGK Toán lớp 8 tập 2: Giải phương trình:

$\frac{x+2}{98}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}}\frac{x+4}{96}=\frac{x+6}{94}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{x+8}{92}\text{\hspace{0.17em}}$

Lời giải:

$$\begin{gathered} \frac{x+2}{98}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}}\frac{x+4}{96}=\frac{x+6}{94}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{x+8}{92} \\ \iff \frac{x+2}{98}\text{\hspace{0.17em}\hspace{0.17em}}+1+\text{\hspace{0.17em}}\frac{x+4}{96}+\text{\hspace{0.17em}}1=\frac{x+6}{94}\text{\hspace{0.17em}\hspace{0.17em}}+1+\frac{x+\text{}8}{92}\text{\hspace{0.17em}\hspace{0.17em}}+1 \\ \iff \frac{x+100}{98}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}}\frac{x+100}{96}=\frac{x+100}{94}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{x+\text{}100}{92} \\ \iff \frac{x+100}{98}\text{\hspace{0.17em}\hspace{0.17em}}-\text{\hspace{0.17em}}\frac{x+100}{94}+\frac{x+100}{96}\text{\hspace{0.17em}\hspace{0.17em}}-\frac{x+\text{}100}{92}=0 \\ \iff (x+100).\left(\frac{1}{98}-\frac{1}{94}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{96}-\frac{1}{92}\right)=0 \\ \iff \left[\begin{array}{c}x+100=0\\ \frac{1}{98}-\frac{1}{94}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{96}-\frac{1}{92}=0\end{array}\right.\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}} \end{gathered}$$

Nếu x + 1000 = 0 thì x = -100

Ta có:

$\frac{1}{98}<\frac{1}{94};\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\frac{1}{96}<\frac{1}{92}\Rightarrow \text{\hspace{0.17em}}\frac{1}{98}-\frac{1}{94}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{1}{96}-\frac{1}{92}<0$

Vậy phương trình có nghiệm x = -100.

Bài 10 trang 131 SGK Toán lớp 8 tập 2: Giải các phương trình:

a) $\frac{1}{x+\text{\hspace{0.17em}}1}-\frac{5}{x-2}=\frac{15}{(x+1).(2-x)}$;

b) $\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{5x-2}{4-x^2}$.

Lời giải:

a) $\frac{1}{x+\text{\hspace{0.17em}}1}-\frac{5}{x-2}=\frac{15}{(x+1).(2-x)}$;

Điều kiện xác định: $x\ne -1;x\ne 2$

Ta có:

$$\begin{gathered} \frac{1}{x+\text{\hspace{0.17em}}1}-\frac{5}{x-2}=\frac{15}{(x+1).(2-x)} \\ \iff \frac{1}{x+\text{\hspace{0.17em}}1}-\frac{5}{x-2}=\frac{-15}{(x+1).(x-2)} \\ \iff \frac{1.(x-2)-5(x+1)}{(x+\text{}1).(x-2)}=\frac{-15}{(x+1).(x-2)} \end{gathered}$$

Suy ra: x – 2 – 5x – 5 = -15

$\iff$x – 2 – 5x – 5 + 15 = 0

$\iff$- 4x  + 8 = 0

$\iff x=2$  (không thỏa mãn điều kiện).

Vậy phương trình đã cho vô nghiệm.

b) $\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{5x-2}{4-x^2}$.

Điều kiện xác định: $x\ne \pm 2$

$\iff \frac{x-1}{x+2}-\frac{x}{x-2}=\frac{-5x+2}{x^2-4}$.

$\iff \frac{(x-1).(x-2)-x(x+\text{}2)}{(x+2).(x-2)}=\frac{-5x+\text{\hspace{0.17em}\hspace{0.17em}}2}{(x+\text{}2).(x-2)}$

Suy ra: (x - 1).(x - 2) – x(x + 2) = -5x + 2

$\iff$x² – 2x – x + 2 – x² – 2x + 5x – 2 = 0

$\iff$0x = 0 nghiệm đúng với mọi x.

Kết hợp với điều kiện xác định,

⇒ phương trình đã cho có nghiệm đúng với mọi x ≠ ±2.

Bài 11 trang 131 SGK Toán lớp 8 tập 2: Giải các phương trình:

a) 3x² + 2x – 1 = 0;

b) $\frac{x-3}{x-2}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{x-2}{x-4}=3\frac{1}{5}$.

Lời giải:

a) 3x² + 2x – 1 = 0;

$\iff$3x² + 3x – x – 1 = 0

$\iff$3x(x + 1) – (x + 1) = 0

$\iff$(x + 1).(3x – 1) = 0

$\iff \left[\begin{array}{c}x+1=0\\ 3x-1=0\end{array}\right.\iff \left[\begin{array}{c}x=-1\\ x=\frac{1}{3}\end{array}\right.$

Vậy phương trình có tập nghiệm $S=\left\{-1;\frac{1}{3}\right\}$.

b) Điều kiện xác định: $x\ne 2;x\ne 4$

$$\begin{gathered} \frac{x-3}{x-2}+\text{\hspace{0.17em}\hspace{0.17em}}\frac{x-2}{x-4}=3\frac{1}{5} \\ \iff \frac{5(x-3)(x-4)}{(x-2)(x-4)}+\text{\hspace{0.17em}}\frac{5{(x-2)}^2}{(x-2)(x-4)} \\ =\frac{16(x-2)(x-4)}{(x-2)(x-4)} \end{gathered}$$

Suy ra: 5(x – 3)(x -  4) + 5(x - 2)² = 16(x - 2).(x - 4)

⇔ 5(x² – 4x – 3x +12) + 5(x² – 4x+ 4) = 16(x² - 4x – 2x + 8)

⇔ 5x² – 35x+ 60 + 5x² - 20x + 20 = 16x² – 96x + 128

⇔ 10x² - 55x + 80 = 16x² – 96x + 128

⇔ 10x² - 55x + 80 - 16x² + 96x - 128 = 0

⇔ -6x² + 41x – 48 = 0

⇔ 6x² - 41x + 48 = 0

⇔ 6x² – 9x – 32x + 48 = 0

⇔ 3x(2x – 3) – 16.(2x – 3) = 0

⇔ (3x – 16)(2x – 3) = 0

$\iff \left[\begin{array}{c}3x-16=0\\ 2x-3=0\end{array}\iff \left[\begin{array}{c}x=\frac{16}{3}\\ x=\frac{3}{2}\end{array}\right.\right.$ ( thỏa mãn điều kiện)

Vậy phương trình có tập nghiệm $S=\left\{\frac{16}{3};\frac{3}{2}\right\}$.

Bài 12 trang 131 SGK Toán lớp 8 tập 2: Một người đi xe máy từ A đến B với vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h nên thời gian về ít hơn thời gian đi là 20 phút. Tính quãng đường AB.

Lời giải:

Gọi độ dài quãng đường AB là x (km), (x > 0, km)

Thời gian đi từ A đến B: $\frac{x}{25}$ (giờ)

Thời gian đi từ B đến A: $\frac{x}{30}$ (giờ)

Thời gian về ít hơn thời gian đi 20 phút = $\frac{1}{3}$ giờ nên ta có phương trình:

$\begin{array}{l}\frac{x}{25}-\frac{x}{30}=\frac{1}{3}\iff \frac{6x-5x}{150}=\frac{50}{150}\\ \\ \iff x=50\end{array}$

Vậy quãng đường AB dài 50km.

Bài 13 trang 131 SGK Toán lớp 8 tập 2: Một xí nghiệp dự định sản xuất 1500 sản phẩm trong 30 ngày. Nhưng nhờ tổ chức lao động hợp lý nên thực tế đã sản xuất mỗi ngày vượt 15 sản phẩm. Do đó xí nghiệp đã sản xuất không những vượt mức dự định 255 sản phẩm mà còn hoàn thành trước thời hạn. Hỏi thực tế xí nghiệp đã rút ngắn được bào nhiêu ngày?

Lời giải:

Theo dự định, mỗi ngày xí nghiệp sản xuất được:

1500 :  30 = 50 (sản phẩm).

Thực tế, mỗi ngày xí nghiệp sản xuất được:

50 + 15 = 65 (sản phẩm)

Tổng số sản phẩm thực tế xí nghiệm sản xuất được:

1500 + 255 = 1755 (sản phẩm)

Thời gian thực tế xí nghiệm sản xuất là:

1755 : 65 = 27 (ngày)

Vậy số ngày được rút ngắn so với dự định là:

30 – 27 = 3 (ngày).

Bài 14 trang 131 SGK Toán lớp 8 tập 2: Cho biểu thức:

$A\text{\hspace{0.17em}\hspace{0.17em}}=\left(\frac{x}{x^2-4}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{2}{2-x}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{1}{x+2}\text{}\right):\text{\hspace{0.17em}\hspace{0.17em}}\left(x-2+\text{\hspace{0.17em}}\frac{10-x^2}{x+2}\right)$

a) Rút gọn biểu thức A;

b) Tính giá trị biểu thức A tại x, biết $\left|x\right|=\frac{1}{2}$;

c) Tìm giá trị của x để A< 0.

Lời giải:

a) Điều kiện: $x\ne \pm 2$

$$\begin{gathered} A\text{\hspace{0.17em}\hspace{0.17em}}=\left(\frac{x}{x^2-4}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{2}{2-x}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{1}{x+2}\text{}\right):\text{\hspace{0.17em}\hspace{0.17em}}\left(x-2+\text{\hspace{0.17em}}\frac{10-x^2}{x+2}\right) \\ =\left(\frac{x}{x^2-4}\text{\hspace{0.17em}\hspace{0.17em}}-\frac{2}{x-2}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{1}{x+2}\text{}\right):\text{\hspace{0.17em}\hspace{0.17em}}\left(x-2+\text{\hspace{0.17em}}\frac{10-x^2}{x+2}\right) \\ =\frac{x-2(x+\text{}2)+\text{}1(x-2)}{(x+\text{}2)(x-2)}:\frac{(x-2).(x+\text{}2)+\text{\hspace{0.17em}}10-x^2}{x+2} \\ =\frac{x-2x-4+\text{}x-2}{(x+\text{}2).(x-2)}:\frac{x^2-4+\text{}10-x^2}{x+\text{\hspace{0.17em}}2} \\ =\frac{-6}{(x+\text{}2).(x-2)}:\text{\hspace{0.17em}\hspace{0.17em}}\frac{6}{x+\text{}2}=\frac{-6}{(x+\text{}2).(x-2)}.\frac{x+\text{\hspace{0.17em}}2}{6} \\ =\frac{-6(x+\text{}2)}{(x+\text{}2)(x-2).6}=\frac{-1}{x-2} \end{gathered}$$

b) Ta có:  $\left|x\right|=\frac{1}{2}\iff x=\pm \frac{1}{2}$ ( thỏa mãn điều kiện).

Trường hợp 1: Với $x=\frac{1}{2}\Rightarrow A=\frac{-1}{\frac{1}{2}-2}=\frac{2}{3}$

Trường hợp 2: Với $x=\frac{-1}{2}\Rightarrow A=\frac{-1}{\frac{-1}{2}-2}=\frac{2}{5}$

c) Để A< 0 thì $\frac{-1}{x-2}<0\iff x-2>\text{\hspace{0.17em}\hspace{0.17em}}0\iff x>2$ (do -1 < 0)

Kết hợp điều kiện, vậy để A < 0 thì x > 2.

Bài 15 trang 131 SGK Toán lớp 8 tập 2: Giải bất phương trình:

$\frac{x-1}{x-3}>\text{\hspace{0.17em}\hspace{0.17em}}1$

Lời giải:

Điều kiện xác định: $x\ne 3$

Ta có: $\frac{x-1}{x-3}>\text{\hspace{0.17em}\hspace{0.17em}}1$

$$\begin{gathered} \iff \frac{x-1}{x-3}-\text{\hspace{0.17em}\hspace{0.17em}}1>0\iff \frac{x-1-(x-3)}{x-3}>0 \\ \iff \frac{x-1-x+3}{x-3}>0\iff \frac{2}{x-3}>0 \\ \iff x-3>\text{\hspace{0.17em}\hspace{0.17em}}0\iff x>3 \end{gathered}$$

Kết hợp điều kiện, để $\frac{x-1}{x-3}>\text{\hspace{0.17em}\hspace{0.17em}}1$ thì x  > 3.

Phần hình học

Bài 1 trang 131 SGK Toán lớp 8 tập 2: Dựng hình thang ABCD (AB // CD), biết ba cạnh: AD = 2cm, CD = 4cm, BC = 3cm và đường chéo AC = 5cm.

Lời giải:

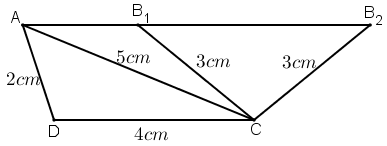
* Dựng hình:

- Dựng tam giác ADC có AD = 2cm, DC = 4cm, CA = 5cm.

- Dựng tia Ax song song với CD.

- Đường tròn (C; 3cm) cắt Ax tại B₁ và B₂.

Hình thang ABCD với B ≡ B₁ hoặc B ≡ B₂ là hình thang cần dựng.

* Chứng minh:

+ Tứ giác ABCD có AD = 2cm, DC = 4cm, CA = 5cm.

+ Ax // CD ⇒ AB // CD ⇒ ABCD là hình thang.

+ Vì  B ∈ (C; 3cm) ⇒ BC = 3cm.

Bài 2 trang 131 SGK Toán lớp 8 tập 2: Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau ở O và tam giác ABO là tam giác đều. Gọi E, F, G theo thứ tự là trung điểm của các đoạn thẳng OA, OD và BC. Chứng minh rằng tam giác EFG là tam giác đều.

Lời giải:

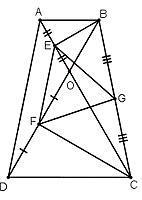
Vì tam giác AOB đều nên: $\widehat{AOB}=\widehat{OAB}=\widehat{OBA}={60}^0$

Vì AB // CD nên $\widehat{OAB}=\widehat{OCD};\widehat{OBA}=\widehat{ODC}$ (các góc so le trong).

Suy ra: $\widehat{OCD}={60}^0;\widehat{ODC}={60}^0$ (1)

Tam giác OCD có: 

$\widehat{OCD}+\widehat{ODC}+\widehat{DOC}={180}^0$ (tổng ba góc của tam giác)  (2).

Từ (1) và (2) suy ra: $\widehat{DOC}={60}^0$ .

Suy ra: tam giác COD là tam giác đều.

Theo giả thiết ΔAOB đều ⇒ BE là đường trung tuyến đồng thời là đường cao

⇒ BE ⊥ AO

⇒ ΔBEC vuông tại E

Mà EG là đường trung tuyến

⇒ $EG=\frac{1}{2}BC$ (3)

Vì ΔCOD đều ⇒ CF là đường trung tuyến đồng thời là đường cao

⇒ CF ⊥ OD

⇒ ΔBFC vuông tại F

Mà FG là đường trung tuyến

⇒  $FG=\frac{1}{2}BC$ (4)

Hình thang ABCD (AB// CD) có: AC = AO + OC = OB + OD = BD

⇒ ABCD là hình thang cân

⇒ AD = BC.

Xét ΔAOD có: AE = EO, FO = FD

⇒ EF là đường trung bình của ΔAOD

⇒ $E\text{}F=\frac{1}{2}AD$

Mà AD = BC (cmt)

⇒ $\text{}EF\text{\hspace{0.17em}\hspace{0.17em}}=\frac{1}{2}\text{}BC$ (5)

Từ (3); (4); (5) suy ra EF = FG = GE ⇒ ΔEFG đều (đpcm).

Bài 3 trang 131 SGK Toán lớp 8 tập 2: Tam giác ABC có các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Tam giác ABC phải có điều kiện gì thì tứ giác BHCK là:

a) Hình thoi?

b) Hình chữ nhật?

Lời giải:

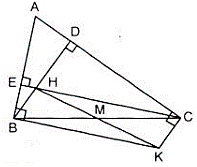
Ta có: CE ⊥ AB (giả thiết)

KB ⊥ AB (giả thiết)

⇒ BK // CE (1)

Tương tự BH // KC (2)

Từ (1) và (2) ⇒ BHCK là hình bình hành.

Gọi M là giao điểm của hai đường chéo BC và HK.

a) Tam giác ABC có hai đường cao BD và CE cắt nhau tại H nên H là trực tâm tam giác ABC

⇒ AH ⊥ BC. (3)

Để tứ giác BHCK là hình thoi

⇔ HM ⊥ BC ( trong đó M là giao điểm của hai đường chéo HK và BC) (4)

Từ (3) và (4) suy ra: A, H, M thẳng hàng.

Khi đó,tam giác ABC có AM là đường cao đồng thời là đường trung tuyến nên tam giác ABC là cân tại A.

b) Để BHCK là hình chữ nhật

$\iff \widehat{HBK}={90}^0\iff \widehat{DBK}=\widehat{ABK}$

Suy ra: D trùng với A.

Khi đó: $\widehat{BAC}={90}^0$

Vậy BHCK là hình chữ nhật khi tam giác ABC vuông tại A.

Bài 4 trang 132 SGK Toán lớp 8 tập 2: Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AN và DM, K là giao điểm BN và CM. Hình bình hình ABCD phải có điều kiện gì để tứ giác MENK là:

a) Hình thoi? ;

b) Hình chữ nhật? ;

c) Hình vuông?

Lời giải:

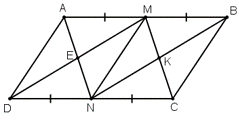
ABCD là hình bình hành ⇒ AB = CD.

Vì M là trung điểm AB ⇒ AM = MB = $\frac{AB}{2}$.

Vì N là trung điểm CD ⇒ CN = DN =  $\frac{CD}{2}$.

⇒ AM = MB = CN = DN.

+ Tứ giác BMDN có: BM // DN và BM = DN

⇒ BMDN là hình bình hành

⇒ DM // BN hay ME // NK

+ Tứ giác AMCN có: AM // NC, AM = NC

⇒ AMCN là hình bình hành

⇒ AN // CM hay EN // MK.

+ Tứ giác MENK có: ME // NK và NE // MK

⇒ MENK là hình bình hành.

a) Để tứ giác MENK là hình thoi

⇔ MN ⊥ EK.

⇔ CD ⊥ AD (Vì EK // CD và MN // AD)

⇔ ABCD là hình chữ nhật.

b) Để tứ giác MENK là hình chữ nhật

⇔ MN = EK

Mà MN = BC; $EK=\frac{1}{2}CD$  (vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).

$\iff BC=\frac{1}{2}CD$

⇔ CD = 2.BC.

c) Để tứ giác MENK là hình vuông

⇔ MENK là hình thoi và đồng thời là hình chữ nhật

⇔ ABCD là hình chữ nhật và có CD = 2.BC.

Bài 5 trang 132 SGK Toán lớp 8 tập 2: Trong tam giác ABC, các đường trung tuyến AA' và BB' cắt nhau ở G. Tính diện tích tam giác ABC biết rằng diện tích tam giác ABG bằng S.

Lời giải:

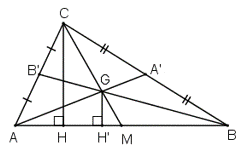
 Kẻ CM là đường trung tuyến, M là trung điểm AB, CM đi qua G

Kẻ CH vuông góc AB và GH’ vuông góc AB

Suy ra: CH // GH’.

Vì CH // GH’ nên ∆MCH $~$∆MGH’.

$\Rightarrow \frac{CH}{GH\text{'}}=\frac{MC}{MG}=\frac{3}{1}=3$

Ta có:

$$\begin{gathered} S_{ABC}=\frac{1}{2}CH.AB;S_{ABG}=\frac{1}{2}GH\text{'}.AB \\ \Rightarrow \frac{S_{ABC}}{S_{ABG}}=\frac{\frac{1}{2}CH.AB}{\frac{1}{2}GH\text{'}.AB}=\frac{CH}{GH\text{'}}=3 \end{gathered}$$

Suy ra: S_ABC = 3S_ABG = 3S.

Vậy S_ABC = 3S.

Bài 6 trang 132 SGK Toán lớp 8 tập 2: Cho tam giác ABC và đường trung tuyến BM. Trên đoạn thẳng BM lấy điểm D sao cho $\frac{BD}{DM}=\frac{1}{2}$. Tia AD cắt BC ở K. Tìm tỉ số diện tích của tam giác ABK và tam giác ABC.

Lời giải:

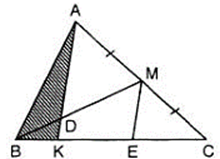
Kẻ ME song song với AK (E ∈ BC).

Ta có:   

$\frac{BK}{KE}=\frac{BD}{DM}=\frac{1}{2}\Rightarrow KE=2BK$

Vì M là trung điểm của AC, ME song song với AK nên ME đi qua trung điểm của KC hay E là trung điểm của KC.

Do đó ME là đường trung bình của tam giác ACK nên EC = KE = 2BK.

Ta có: BC = BK + KE + EC = 5BK nên $\frac{BK}{BC}=\frac{1}{5}$.

Ta có:

$S_{ABK}=\frac{1}{2}{h}_a.BK;S_{ABC}=\frac{1}{2}{h}_a.BC$

( trong đó h_a là độ dài đường cao xuất phát từ đỉnh A)

Suy ra:

 $$\begin{gathered} \frac{S_{ABK}}{S_{ABC}}=\frac{\frac{1}{2}{h}_a.BK}{\frac{1}{2}{h}_a.BC} \\ =\frac{BK}{BC}=\frac{1}{5} \end{gathered}$$

Bài 7 trang 132 SGK Toán lớp 8 tập 2: Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE.

Lời giải:

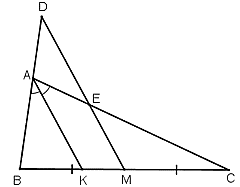
Vì AK là đường phân giác của tam giác ABC nên:

$\frac{KB}{AB}=\frac{KC}{AC}$  (1)

Ta có: MD // AK

⇒ ΔABK $~$  ΔDBM và ΔECM $~$  ΔACK

$\Rightarrow \frac{KB}{AB}=\frac{BM}{BD};\frac{CM}{CE}=\frac{KC}{AC}$  (2)

Từ (1) và (2) ta có: 

  $\frac{BM}{BD}=\frac{CM}{CE}$ (3)

Do BM = CM (giả thiết) nên từ (3) suy ra: BD = CE ( đpcm).

Bài 8 trang 132 SGK Toán lớp 8 tập 2: Trên hình 151 cho thấy ta có thể xác định chiều rộng BB' của khúc sông bằng cách xét hai tam giác đồng dạng ABC và AB'C'. Hãy tính BB' nếu AC = 100m, AC' = 32cm, AB' = 34m.

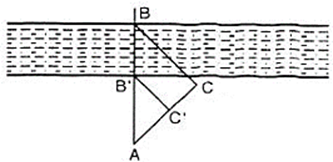
Hình 151

Lời giải:

Ta có: BC// C’C’ nên

 $\frac{AB\text{'}}{BB\text{'}}=\frac{AC\text{'}}{CC\text{'}}$ (định lí Ta – let)

Suy ra: $BB\text{'}=\frac{AB\text{'}.\text{\hspace{0.17em}\hspace{0.17em}}CC\text{'}}{AC\text{'}}$

Mà AB’ = 34;  AC’ = 32

Suy ra:  CC’ = AC – AC’ = 100 – 32 = 68.

Suy ra: $B\text{}B\text{'}=\frac{34.68}{32}=72,25m$.

Bài 9 trang 132 SGK Toán lớp 8 tập 2: Cho tam giác ABC có AB < AC, D là một điểm nằm giữa A và C. Chứng minh rằng: $\widehat{ABD}=\widehat{ACB}\iff A{B}^2=AC.AD$.

Lời giải:

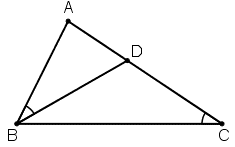
Ta chứng minh hai chiều:

a) Giả sử $\widehat{AB\text{}D}=\widehat{A\text{}CB}$. Chứng minh: AB² = AC. AD.

Xét ∆ABD và ∆ACB có:

$\widehat{A}chung;\widehat{ABD}=\widehat{ACB}$

Suy ra: ∆ABD $~$ ∆ACB ( g.g)

Suy ra: $\frac{AB}{AC}=\frac{AD}{AB}\Rightarrow A{B}^2=AC.AD$

b) Ngược lại: giả sử AB² = AC. AD. Ta chứng minh

$\widehat{AB\text{}D}=\widehat{A\text{}CB}$.

Theo giả thiết AB² = AC. AD nên

 $\frac{AB}{AD}=\frac{AC}{AB}$

Xét ∆ABD và ∆ACB có:

$\widehat{A}chung$

$\frac{AB}{AD}=\frac{AC}{AB}$

Suy ra: ∆ABD $~$ ∆ACB

Do đó,  $\widehat{AB\text{}D}=\widehat{A\text{}CB}$.

Vậy từ a và b suy ra: $\widehat{ABD}=\widehat{ACB}\iff A{B}^2=AC.AD$.

Bài 10 trang 132 SGK Toán lớp 8 tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.

a) Chứng minh rằng các tứ giác ACC’A', BDD'B' là những hình chữ nhật.

b) Chứng minh rằng AC'² = AB² + AD² + AA'².

c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.

Lời giải:

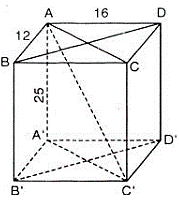
a) ABCD.A’B’C’D’ là hình hộp chữ nhật

⇒ AA’ // CC’, AA’ = CC’

⇒ AA’C’C là hình bình hành

Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC

⇒ $\widehat{A\text{'}AC}={90}^0$ .

⇒ Hình bình hành AA’C’C là hình chữ nhật.

Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật

b) Áp dụng định lý Pytago:

Trong tam giác vuông ACC’ ta có:

AC’² = AC² + CC’² = AC² + AA’²

Trong tam giác vuông ABC ta có:

AC² = AB² + BC² = AB² + AD²

Do đó: AC’² =AB² + AD² + AA’².

c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.

Diện tích xung quanh:

Sxq = 2.(AB + AD).AA’

= 2.(12 + 16).25 = 1400 (cm² )

Diện tích một đáy:

S_đ = AB.AD  = 12.16 = 192 (cm² )

Diện tích toàn phần:

S_tp = S_xq + 2S_đ = 1400 + 2.192 = 1784 (cm² )

Thể tích:

V = AB.AD.AA’ = 12.16.25 =  4800 (cm³ )

Bài 11 trang 132 SGK Toán lớp 8 tập 2: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20cm, cạnh bên SA = 24cm.

a) Tính chiều cao SO rồi tính thể tích của hình chóp.

b) Tính diện tích toàn phần của hình chóp.

Lời giải:

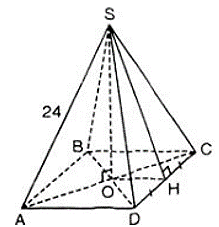
a) Vì S.ABCD là hình chóp tứ giác đều

⇒ ABCD là hình vuông

⇒ AC = $AB\sqrt{2}=20\sqrt{2}$  (cm).

Gọi O là giao điểm của AC và BD.

Suy ra:  SO ⊥ (ABCD)

⇒ SO ⊥ AO

⇒ ΔSAO vuông tại O

⇒ SO² + OA² = SA² (định lý Py – ta – go)

⇒ SO² = SA² – OA² 

$$\begin{gathered} =S{A}^2-{\left(\frac{AC}{2}\right)}^2 \\ ={24}^2-{\left(\frac{20\sqrt{2}}{2}\right)}^2 \\ =376 \end{gathered}$$

⇒ $SO=\sqrt{376}cm$

Thể tích hình chóp:

$$\begin{gathered} V=\frac{1}{3}.SO.S_{ABCD} \\ =\frac{1}{3}.\sqrt{376}.{20}^2 \\ \approx 2585,43c{m}^3 \end{gathered}$$

b) Gọi H là trung điểm của CD, do SABCD là hình chóp tứ giác đều nên tam giác SCD là tam giác cân, do đó SH vừa là đường trung tuyến vừa là đường cao

SH² = SD² – DH² = 24² – ${\left(\frac{20}{2}\right)}^2$ = 476

⇒ SH = $\sqrt{476}$  ≈ 21,8 (cm)

⇒ S_xq = p.d = 2.AB.SH = 2.20. $\sqrt{476}$ ≈ 872,7 (cm²).

S_đ = AB² = 20² = 400 (cm²)

⇒ S_tp = S_xq + S_đ = 872,7 + 400 = 1272,7 (cm²).