Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều hay, chi tiết giúp học sinh dễ dàng làm bài tập Diện tích xung quanh của hình chóp đều lớp 8.

Giải bài tập Toán lớp 8 Bài 8: Diện tích xung quanh của hình chóp đều

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 119 Toán 8 Tập 2: Vẽ, cắt và gấp miếng bìa như ở hình 123. Quan sát hình gấp được, hãy điền số thích hợp vào chỗ trống (…) ở các câu dưới đây:

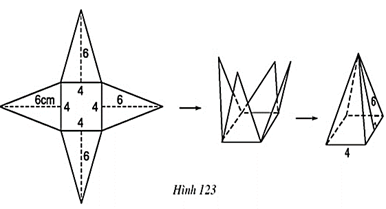
a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là …

b) Diện tích mỗi mặt tam giác là … cm².

c) Diện tích đáy của hình chóp đều là … cm².

d) Tổng diện tích tất cả các mặt bên của hình chóp đều là … cm².

Lời giải:

a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4

b) Diện tích mỗi mặt tam giác là $\frac{1}{2}$ . 4.6 = 12 cm².

c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm².

d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm².

Bài tập (trang 121)

Bài 40 trang 121 Toán 8 Tập 2: Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích toàn phần của hình chóp.

Lời giải:

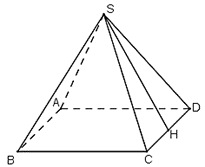
Gọi H là trung điểm của CD

Vì ΔSCD cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao

⇒ SH ⊥ CD.

Ta có:

$\begin{array}{l}CH=HD=\frac{CD}{2}=\frac{30}{2}=15\\ d=SH=\sqrt{S{C}^2-C{H}^2}\\ \hspace{0.17em}=\sqrt{{25}^2-{15}^2}=20cm\end{array}$

Chu vi đáy là: 4. 30 = 120 (cm)

Diện tích xung quanh của hình chóp:     

$S_{xq}=p.d=\frac{1}{2}\mathrm{.120.20}=1200c{m}^2$

Diện tích đáy: S_d = 30² = 900 (cm²)

Diện tích toàn phần của hình chóp:

S_tp = S_xq + S_d = 1200 + 900 = 2100 (cm²)

Bài 41 trang 121 Toán 8 Tập 2: Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.

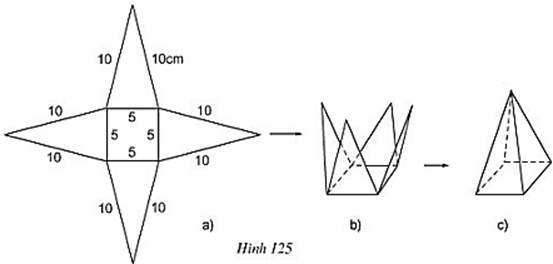
a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?

b) Sử dụng định lí Pi – ta - go để tính chiều cao ứng với đáy của mỗi tam giác.

c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?

Lời giải:

a) Trong hình 125a có 4 tam giác cân bằng nhau.

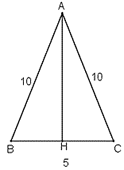
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.

Ta có: $HC=HB=\frac{1}{2}BC=\frac{5}{2}cm$

Chiều cao ứng với đáy của mỗi tam giác: 

$$\begin{gathered} AH=\sqrt{A{C}^2-H{C}^2} \\ =\sqrt{{10}^2-{\left(\frac{5}{2}\right)}^2} \\ =\frac{5\sqrt{15}}{2} \end{gathered}$$

c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).

Diện tích xung quanh hình chóp:

$$\begin{gathered} S_{xq}=p.d \\ =\frac{1}{2}\mathrm{.20.}\frac{5\sqrt{15}}{2} \\ =25\sqrt{15} cm2 \end{gathered}$$

Diện tích đáy:

S_d = 5² = 25 (cm²)

Diện tích toàn phần của hình chóp:

S_tp = S_d + S_xq 

= 25 + 25$\sqrt{15}$ $\approx$  121,8 (cm²)

Bài 42 trang 121 Toán 8 Tập 2: Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên hình 125.

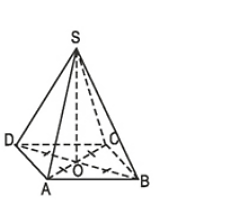
Lời giải:

Gọi O là giao điểm của AC và BD.

Áp dụng định lí Py – ta - go vào tam giác ABC ta được

AC² = AB²  + BC² = 5² + 5² = 50

$\Rightarrow AC=5\sqrt{2}$cm

Do O là trung điểm của AC nên:

$AO=OC=\frac{1}{2}AC=\frac{5\sqrt{2}}{2}cm$

Tam giác SAO vuông tại O nên:

$S{A}^2=S{O}^2+O{A}^2$

$\Rightarrow$SO² = SA² – AO²  

$$\begin{gathered} \iff SO={10}^2-{\left(\frac{5\sqrt{2}}{2}\right)}^2=\frac{175}{2} \\ \Rightarrow SO=\sqrt{\frac{175}{2}}=\frac{5\sqrt{14}}{2}cm \end{gathered}$$

Vậy độ dài đường cao của hình chóp là $\frac{5\sqrt{14}}{2}cm$.

Bài 43 trang 121 Toán 8 Tập 2: Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (h.126).

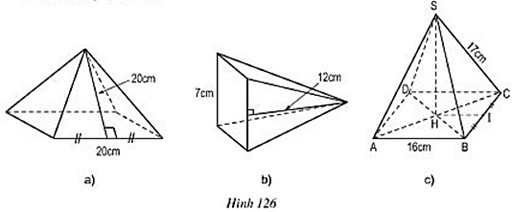
Lời giải:

Diện tích xung quanh:

Hình a:

$S_{xq}=p.d=\frac{1}{2}\mathrm{.20.4.}20=800c{m}^2$

(trong đó chu vi đáy là 20.4 cm)

Diện tích đáy: S_d = 20² = 400 (cm²)

Diện tích toàn phần:

S_tp = S_xq + S_đ = 800 + 400 = 1200 (cm²)

Hình b:

Chu vi đáy là 4.7 = 28 (cm)

Diện tích xung quanh là:

$S_{xq}=p.d=\frac{1}{2}\mathrm{.28.12}=168c{m}^2$

S_d = 7² = 49 cm²

S_tp = 168 + 49 = 217 cm²

Hình c:

+) Diện tích đáy là S_d = 16² = 256 (cm² ).

Do I là trung điểm của BC nên

$IB=IC=\frac{BC}{2}=8cm$.

+) Tam giác SBC có SI là đường trung tuyến nên đồng thời là đường cao.

Ta có:

 $$\begin{gathered} d=SI=\sqrt{S{C}^2-C{I}^2} \\ =\sqrt{{17}^2-8^2}=15cm \end{gathered}$$

+) Chu vi đáy là: 16 .4 = 64 (cm)

+) Diện tích xung quanh là:

$S_{xq}=p.d=\frac{1}{2}.64.15=480c{m}^2$.

+) Diện tích toàn phần là:

S_tp = S_đ + S_xq = 256 + 480 = 736 (cm²).