Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 6: Giải bài toán bằng cách lập phương trình hay, chi tiết giúp học sinh dễ dàng làm bài tập Giải bài toán bằng cách lập phương trình lớp 8.

Giải bài tập Toán lớp 8 Bài 6: Giải bài toán bằng cách lập phương trình

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 24 Toán 8 Tập 2: Giả sử hằng ngày bạn Tiến dành x phút để tập chạy. Hãy viết biểu thức với biến x biểu thị:

a) Quãng đường Tiến chạy được trong x phút, nếu chạy với vận tốc trung bình là 180m/ph.

b) Vận tốc trung bình của Tiến (tính theo km/h), nếu trong x phút Tiến chạy được quãng đường là 4500m.

Lời giải

a) Quãng đường Tiến chạy được là:

S = vt = 180x (m)

b) Đổi 4 500m = 4,5km.

x phút =  $\frac{x}{60}$giờ.

Vận tốc trung bình của Tiến là: 

v = $\frac{S}{t}$= $4,5:\text{\hspace{0.17em}\hspace{0.17em}}\frac{x}{60}=\frac{270}{x}(\text{}km/h)$.

Câu hỏi 2 trang 24 Toán 8 Tập 2: Gọi x là số tự nhiên có hai chữ số (ví dụ x = 12). Hãy lập biểu thức biểu thị số tự nhiên có được bằng cách:

a) Viết thêm chữ số 5 vào bên trái số x (ví dụ 12 → 512, tức là 500 + 12);

b) Viết thêm chữ số 5 vào bên phải số x (ví dụ 12 → 125, tức là 12 10 + 5).

Lời giải

a) Số tự nhiên mới khi viết thêm chữ số 5 vào bên trái chữ số tự nhiên cũ là: 5.100 + x

b) Số tự nhiên mới khi viết thêm chữ số 5 vào bên phải chữ số tự nhiên cũ là: 10x + 5

Câu hỏi 3 trang 25 Toán 8 Tập 2: Giải bài toán trong Ví dụ 2 bằng cách chọn x là số chó.

Lời giải

Gọi số x là chó, với điều kiện x là số nguyên dương và nhỏ hơn 36

Khi đó, số chân chó là 4x

Vì cả gà và chó là 36 con nên số gà là 36 – x và số chân gà là 2(36 – x)

Tổng số chân là 100 nên ta có phương trình:

4x + 2(36 – x) = 100

⇔ 4x + 72 - 2x = 100

⇔ 2x = 28

⇔ x = 14 (thỏa mãn các điều kiện của ẩn)

Vậy số chó là 14(con)

⇒ Số gà là: 36 – 14 = 22(con)

Bài tập (trang 25; 26)

Bài 34 trang 25 Toán 8 Tập 2: Mẫu số của một phân số lớn hơn tử số của nó là 3 đơn vị. Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới bằng $\frac{1}{2}$. Tìm phân số ban đầu.

Lời giải:

Gọi x là tử số của phân số $(x\in \mathbb{Z};x\ne -3)$

Vì mẫu hơn tử số 3 đơn vị nên mẫu số là: x + 3.

Phân số ban đầu là $\frac{x}{x+3}$

Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới là

$\frac{x+\text{\hspace{0.17em}}2}{x+3+2}=\frac{x+2}{x+\text{\hspace{0.17em}\hspace{0.17em}}5}\text{v}$

Theo giả thiết ta có: $\frac{x+\text{\hspace{0.17em}}2}{x+\text{\hspace{0.17em}}5}=\frac{1}{2}$

Suy ra: 2(x + 2) = 1.(x + 5)

$\iff$ 2x +  4 = x + 5

$\iff$x = 1 ( thỏa mãn điều kiện)

Vậy phân số ban đầu là $\frac{1}{4}$.

Bài 35 trang 25 Toán 8 Tập 2: Học kì một, số học sinh giỏi của lớp 8A bằng $\frac{1}{8}$ số học sinh cả lớp. Sang học kì hai, có thêm 3 bạn phấn đấu trở thành học sinh giỏi nữa, do đó số học sinh giỏi bằng 20% số học sinh cả lớp. Hỏi lớp 8A có bao nhiêu học sinh?

Lời giải:

Gọi số học sinh của lớp 8A là x (x ∈ N*; x > 3).

Số học sinh giỏi của học kì I là : $\frac{1}{8}x$   ( học sinh)

Sang học kì 2, số học sinh giỏi bằng 20% số học sinh cả lớp nên số học sinh giỏi của học kì II là :  

$20\%x=\frac{20}{100}x=\frac{1}{5}x$

Vì số học sinh giỏi của học kì II nhiều hơn số HSG của học kì I 3 học sinh nên ta có phương trình:

$$\begin{gathered} \frac{1}{5}x-\frac{1}{8}x=3 \\ \iff \frac{8x-5x}{40}=\frac{120}{40} \\ \iff 8x-5x=120 \end{gathered}$$

$\iff$3x = 120

 $\iff x=40$(thỏa mãn điều kiện).

Vậy lớp 8A có 40 học sinh.

Bài 36 trang 26 Toán 8 Tập 2: (Bài toán nói về cuộc đời nhà toán học Đi-ô-phăng, lấy trong Hợp tuyển Hy Lạp - Cuốn sách gồm 46 bài toán về số, viết dưới dạng thơ trào phúng).

Thời thơ ấu của Đi - ô - phăng chiếm $\frac{1}{6}$ cuộc đời, $\frac{1}{12}$ cuộc đời tiếp theo là thời thanh niên sôi nổi. Thêm $\frac{1}{7}$ cuộc đời nữa của ông sống độc thân. Sau khi lập gia đình được 5 năm thì sinh một con trai.Nhưng số mệnh chỉ cho con sống bằng nửa đời cha. Ông đã từ trần 4 năm sau khi con trai mất. Đi- ô- phăng sống bao nhiêu tuổi. Hãy tính cho ra?

Lời giải:

Gọi x là số tuổi của ông Đi - ô - phăng (x > 0, x ∈ ).

Thời thơ ấu của ông là $\frac{1}{6}x$ ( uổi)

Thời thanh niên là $\frac{1}{12}x$ (tuổi)

Thời gian ông sống độc thân $\frac{1}{7}x$ (tuổi).

Thời gian lập gia đình đến khi có con và mất là $5+\frac{1}{2}x+\text{\hspace{0.17em}\hspace{0.17em}}4$.

Ta có phương trình:

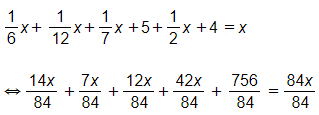
$\iff$14x + 7x + 12x + 42x + 756 = 84x

$\iff$-9x = -756

$\iff$x = 84 (thỏa mãn điều kiện).

Vậy nhà toán học Đi-ô-phăng thọ 84 tuổi.