Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 4: Đường trung bình của tam giác, của hình thang hay, chi tiết giúp học sinh dễ dàng làm bài tập Đường trung bình của tam giác, của hình thang lớp 8.

Giải bài tập Toán lớp 8 Bài 4: Đường trung bình của tam giác, của hình thang

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 76 Toán 8 Tập 1: Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.

Lời giải

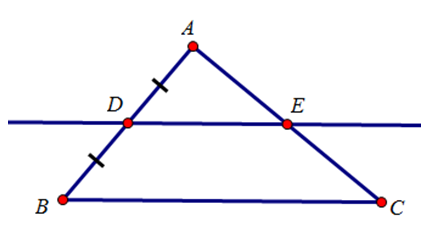
Dự đoán: E là trung điểm cạnh AC

Câu hỏi 2 trang 77 Toán 8 Tập 1: Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB, trung điểm E của AC. Dùng thước đo góc và thước chia khoảng để kiểm tra rằng $\widehat{ADE}=\widehat{B}, DE=\frac{1}{2}BC$.

Lời giải

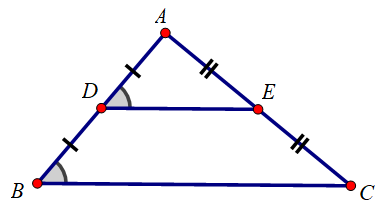
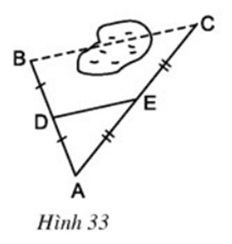
Câu hỏi 3 trang 77 Toán 8 Tập 1: Tính độ dài đoạn BC trên hình 33.

Giữa hai điểm B và C có chướng ngại vật (h.33). Biết DE = 50m, ta có thể tích được khoảng cách giữa hai điểm B và C.

Lời giải

Xét $\Delta ABC,$ có:

D là trung điểm AB

E là trung điểm AC

Suy ra DE là đường trung bình của

$\Rightarrow DE=\frac{1}{2}BC$ hay BC = 2DE.

Mà DE = 50m nên BC = 2.50 = 100m.

Vậy khoảng cách giữa hai điểm B và C là 100m.

Câu hỏi 4 trang 78 Toán 8 Tập 1: Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F (h.37). Có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC ?

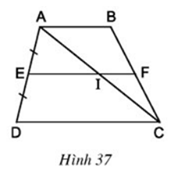
Lời giải

Áp dụng định lí 1 đường trung bình của tam giác

ΔADC có E là trung điểm AD và EI song song với cạnh DC

⇒ Điểm I là trung điểm AC

ΔABC có I là trung điểm AC và FI song song với cạnh AB

⇒ điểm F là trung điểm BC

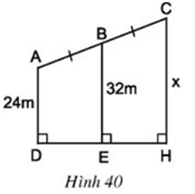
Câu hỏi 5 trang 79 Toán 8 Tập 1: Tính x trên hình 40.

Lời giải

Dựa vào hình vẽ ta thấy rằng AD ⊥ DH, CH ⊥ DH, BE ⊥ DH

Suy ra, AD // BE // CH

Xét tứ giác ADHC có: AC // CH nên ADHC là hình thang.

Ta lại có B là trung điểm của AC và BE // AD // CH

$\Rightarrow$E là trung điểm của BH

Suy ra BE là đường trung bình của hình thang ADHC.

$\begin{array}{l}\Rightarrow BE=\frac{AD+CH}{2}\\ \iff 32=\frac{24+x}{2}\\ \iff 32.2=24+x\\ \iff 64=24+x\\ \iff x=64-24=40.\end{array}$

Bài tập (trang 79, 80)

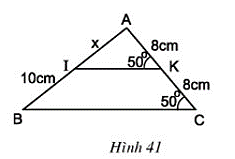
Bài 20 trang 79 Toán 8 Tập 1:Tính x trên hình 41.

Lời giải

Ta có: $\widehat{AKI}=\widehat{C}=50°$

Mà hai góc ở vị trí hai góc đồng vị

⇒ IK // BC

Ta lại có KA = KC (= 8cm) nên K là trung điểm AC

Xét tam giác ABC, có:

Đường thẳng IK đi qua trung điểm cạnh AC và song song với cạnh BC nên đi qua trung điểm cạnh AB

⇒ I là trung điểm AB

⇒ IA = IB = 10cm hay x = 10cm.

Bài 21 trang 79 Toán 8 Tập 1: Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và CD = 3cm.

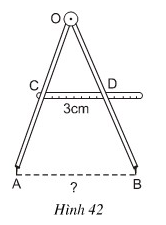
Lời giải

Xét $\Delta OAB$, ta có:

C là trung điểm của OA

D là trung điểm của OB

⇒ CD là đường trung bình của ΔOAB

⇒ $CD=\frac{1}{2}AB$.

⇒ AB = 2CD = 2.3 = 6cm.

Vậy AB = 6cm.

Bài 22 trang 80 Toán 8 Tập 1: Cho hình 43. Chứng minh rằng AI = IM.

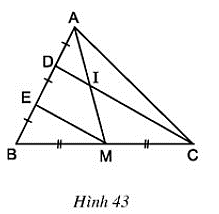
Lời giải

ΔBDC có

BE = ED nên E là trung điểm của BD

BM = CM nên M là trung điểm của BC

⇒ EM là đường trung bình của ΔBDC

⇒ EM // DC hay EM // DI.

ΔAEM có DI // EM (cmt) và AD = DE (gt)

⇒ IA = IM (Theo định lý 1)

Bài 23 trang 80 Toán 8 Tập 1: Tìm x trên hình 44.

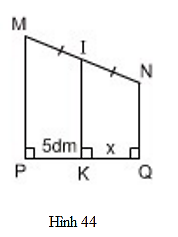
Lời giải

Ta có:

$\left.\begin{array}{l}MP\perp PQ\\ IK\perp PQ\\ NQ\perp PQ\end{array}\right\}\Rightarrow MP//IK//NQ$

Xét tứ giác MNQP, có: MP // NQ

$\Rightarrow$ Tứ giác MPQN là hình thang

Do đường thẳng IK đi qua trung điểm cạnh bên MN và song song với hai đáy nên K là trung điểm PQ.

Nên PK = KQ =5dm

Vậy x = 5dm

Bài 24 trang 80 Toán 8 Tập 1: Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.

Lời giải

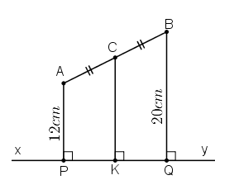
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.

Ta có: $\left.\begin{array}{l}AP\perp xy\\ CK\perp xy\\ BQ\perp xy\end{array}\right\}\Rightarrow AP//CK//BQ$

Xét tứ giác ABQP có AP // BQ

⇒ Tứ giác ABQP là hình thang.

Hình thang ABQP có:

AC = CB (gt) và CK // AP // BQ

⇒ PK = KQ

⇒ CK là đường trung bình của hình thang

⇒ $CK=\frac{AP+BQ}{2}$.

Mà AP = 12cm, BQ = 20cm

$CK=\frac{12+20}{2}=\frac{32}{2}=16cm.$

Vậy khoảng cách từ trung điểm C của AB đến xy bằng CK và bằng: 16cm.

Bài 25 trang 80 Toán 8 Tập 1: Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

Lời giải

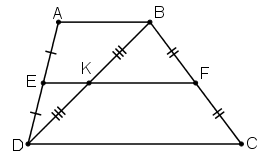
Xét ΔABD có:

D là trung điểm AB

K là trung điểm BD

⇒ EK là đường trung bình của ΔDAB

⇒ EK // AB

Xét hình thang ABCD có:

E là trung điểm của AB

F là trung điểm của BC

⇒ EF là đường trung bình của hình thang ABCD

⇒ EF // AB// CD

Qua điểm E ta có EK // AB và EF // AB nên theo tiên đề Ơclit ta có E, K, F thẳng hàng.

Bài 26 trang 80 Toán 8 Tập 1:Tính x, y trên hình 45 trong đó AB // CD // EF // GH.

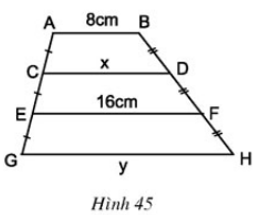
Lời giải

+) Tính x:

Xét tứ giác ABFE, có: AB // EF nên tứ giác ABFE là hình thang

Hình thang ABFE có:

CA = CE nên C là trung điểm của AE

DB = DF nên D là trung điểm của BF

⇒ CD là đường trung bình của hình thang ABFE

$$\begin{gathered} \Rightarrow CD=\frac{AB+\text{EF}}{2} \\ \Rightarrow CD=\frac{8+16}{2}=\frac{24}{2}=12cm. \end{gathered}$$

+ Tính y:

Vì CD // GH nên tứ giác CDHG là hình thang

Hình thang CDHG có:

EC = EG nên E là trung điểm của CG

FD = FH nên F là trung điểm của DH

⇒ EF là đường trung bình của hình thang CDHG

$\Rightarrow FE=\frac{CD+GH}{2}=\frac{12+y}{2}$

Mà EF = 16cm $\Rightarrow 16=\frac{CD+GH}{2}=\frac{12+y}{2}$

$\begin{array}{l}\Rightarrow 16.2=12+y\\ \Rightarrow 32=12+y\\ \Rightarrow y=32-12=20cm.\end{array}$

Vậy x = 12cm và y = 20cm.

Bài 27 trang 80 Toán 8 Tập 1: Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.

a) So sánh các độ dài EK và CD, KF và AB

b) Chứng minh rằng $\text{EF}\le \frac{AB+CD}{2}.$

Lời giải

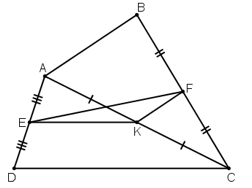
a) + Xét ΔADC có:

E là trung điểm của AD

K là trung điểm của AC

⇒ EK là đường trung bình của ΔADC

$\Rightarrow EK=\frac{CD}{2}$

+ Xét ΔABC có:

K là trung điểm AC

F là trung điểm BC

⇒ KF là đường trung bình của ΔABC

$\Rightarrow KF=\frac{AB}{2}.$

b) Xét $\Delta FEK$, có: EF < EK + KF (Bất đẳng thức tam giác)

Hơn nữa nếu EF = EK + KF

$\iff$ E, K, F thẳng hàng $\iff$AB // CD.

Do đó: EF ≤ EK + KF

Bài 28 trang 80 Toán 8 Tập 1: Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.

a) Chứng minh rằng AK = KC, BI = ID.

b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.

Lời giải

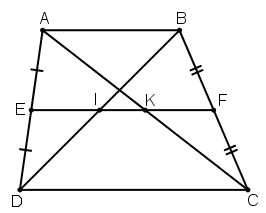
a) + Xét hình thang ABCD có:

E là trung điểm của AD (gt)

F là trung điểm của BC (gt)

⇒ EF là đường trung bình của hình thang ABCD.

⇒ EF // AB // CD

+ Xét ΔABC có:

F là trung điểm BC (gt)

FK // AB (cmt)

⇒ K là trung điểm của AC hay AK = KC.

+ Xét ΔABD có:

E là trung điểm của AD (gt)

EI // AB (cmt)

⇒ I là trung điểm của BD hay BI = ID

b) + Xét hình thang ABCD có:

EF là đường trung bình của hình thang ABCD.

$$\begin{gathered} \Rightarrow EF=\frac{AB+CD}{2} \\ =\frac{6+10}{2}=\frac{16}{2}=8cm \end{gathered}$$

+ Xét ΔABD có:

FK là đường trung bình của tam giác ABC

⇒ $FK=\frac{1}{2}AB=\frac{1}{2}.6=3cm.$

+ Xét ΔABD có:

EI là đường trung bình của tam giác ABD

$\Rightarrow EI=\frac{1}{2}AB=\frac{1}{2}.6=3cm.$

Mặt khác: FK + IK + IE = EF

$\Rightarrow$IK = EF – FK – IE

$\Rightarrow$IK = 8 – 3 – 3 = 2 cm.