Đường trung bình của tam giác, của hình thang

Tưởng Thị Hồng Vân Ngày: 08-03-2024 Lớp 8

Tải xuống 13 3 K 19

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập về Đường trung bình của tam giác, của hình thang Toán lớp 8, tài liệu bao gồm 13 trang, tuyển chọn các bài tập Đường trung bình của tam giác, của hình thang có lý thuyết và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Đường trung bình của tam giác, của hình thang gồm các nội dung chính sau:

I. Phương pháp giải

- tóm tắt lý thuyết ngắn gọn;

- tính chất và phương pháp giải chi tiết từng dạng bài tập.

II. Một số ví dụ/ Ví dụ minh họa

- gồm 4 ví dụ minh họa đa dạng của các dạng bài tập trên có lời giải chi tiết.

III. Bài tập vận dụng

- gồm 16 bài tập vận dụng (16 bài tập có đáp án và lời giải chi tiết) giúp học sinh tự rèn luyện cách giải các dạng bài tập Đường trung bình của tam giác, của hình thang.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây: Đường trung bình của tam giác, của hình thang (ảnh 1)

Đường trung bình của tam giác, của hình thang

I. Phương pháp giải

1. Định nghĩa

· Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác (h.3.1)

· Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang (h.32)

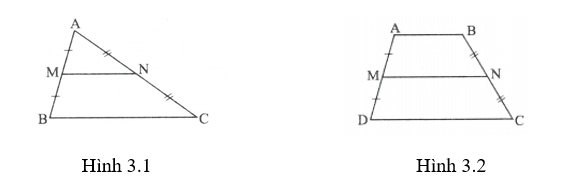
Đường trung bình của tam giác, của hình thang (ảnh 2)

2. Tính chất

· Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Trên hình 3.1 thì $M N // B C$ và $M N = \frac{B C}{2}$

· Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.

Trên hình 3.2 thì $M N // A B // C D$ và $M N = \frac{A B + C D}{2}$

3. Định lí

· Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba

· Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của cạnh bên thứ hai

I. Một số ví dụ

Ví dụ 1. Cho tứ giác $A B C D$ . Gọi M và N lần lượt là trung điểm của AB và . Gọi G là trọng tâm của tam giác BCD. Chứng minh rằng AG chia đôi MN .

Giải (h.3.3)

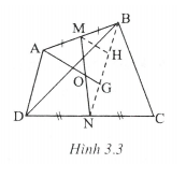
* Tìm cách giải

Kết luận của bài toán gợi ý cho ta dùng định lý đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba. Gọi H là trung điểm của BG thì ta có thể dùng định lý đường trung bình để chứng minh.

* Trình bày lời giải

Gọi O là giao điểm của AG và MN.

Gọi H là trung điểm của BG .

Theo tính chất của trọng tâm, ta có: BH = HG = GN.

Xét $Δ A B G$ có $M H$ là đường trung bình $\Rightarrow M H // A G$ .

Xét $Δ H M N$ có $A G // M H$ và $N G = G H$ nên $O N = O M$ .