Với giải sách bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 12. Mời các bạn đón xem:
Giải SBT Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số
Bài 1 trang 10 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng xét dấu của đạo hàm f'(x) như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (−∞; 0).
B. (2; +∞).
C. (−∞; 2).
D. (0; 2).
Lời giải:
Đáp án đúng là: A
Căn cứ vào bảng xét dấu của hàm số, ta có:
Hàm số nghịch biến trên các khoảng (−∞; 0) và (1; 2).
Bài 2 trang 10 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (−2; 0).
B. (4; +∞).
C. (−∞; 0).
D. (−2; −1).
Lời giải:
Đáp án đúng là: D
Căn cứ vào bảng biến thiên của hàm số, ta có:
Hàm số đồng biến trên các khoảng (−2; −1) và (−1; 0).
Bài 3 trang 10 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm f'(x)= −x(2x – 5), ∀x ∈ ℝ. Khẳng định nào dưới đây đúng?
A. f(−2) < f(−1).
B. f(0) > f(2).
C. f(3) > f(5).
D. f(3) > f(2).
Lời giải:
Đáp án đúng là: C
Theo đề, ta có: f'(x) = −x(2x – 5) với ∀x ∈ ℝ.
f'(x) = 0 ⇔ −x(2x – 5) = 0 ⇔ x = 0 hoặc x = .
Bảng biến thiên của hàm số:
Căn cứ vào bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng ;
Hàm số nghịch biến trên khoảng (−∞; 0) và .
Xét các đáp án:
Có −2, −1 ∈ (−∞; 0) và −2 < −1 nên f(−2) > f(−1) ⇒ A sai.
Có 2 ∈ và 0 < 2 nên f(0) < f(2) ⇒ B sai.
Có 3, 5 ∈ và 3 < 5 nên f(3) > f(5) ⇒ C đúng.
Có 2, 3 thuộc hai khoảng khác nhau nên ta chưa thể đánh giá được ⇒ D sai.
Bài 4 trang 11 SBT Toán 12 Tập 1: Cho hàm số y = −x3 + 3x2 − 4. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng (0; 2).
B. Hàm số nghịch biến trên khoảng (−∞; 2).
C. Hàm số đồng biến trên khoảng (0; +∞).
D. Hàm số nghịch biến trên khoảng (0; 2).
Lời giải:
Đáp án đúng là: A
Ta có: y = −x3 + 3x2 − 4 ⇒y' = −3x2 + 6x.
y' = 0 ⇔ −3x2 + 6x = 0 ⇔ x = 0 hoặc x = 2.
Bảng biến thiên của hàm số:
Căn cứ vào bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng (0; 2);
Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).
Bài 5 trang 11 SBT Toán 12 Tập 1: Cho hàm số . Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng (−∞; 1) và (1; +∞).
B. Hàm số nghịch biến trên ℝ.
C. Hàm số đồng biến trên ℝ.
D. Hàm số nghịch biến trên khoảng (−∞; 1) và (1; +∞).
Lời giải:
Đáp án đúng là: D
Tập xác định: D = ℝ\{1}.
Ta có: ⇒ .
Suy ra y' < 0 với ∀ x ∈ D.
Vậy hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).
Bài 6 trang 11 SBT Toán 12 Tập 1: Trong các hàm số sau, hàm số đồng biến trên ℝ là:
A. y = x − .
B. y = 2x3 − x2 + 5x + 1.
C. y = x4 + 2x2 − 3.
D. y = 2x2 + 3.
Lời giải:
Đáp án đúng là: B
Xét các đáp án, ta thấy:
Đáp án A hàm số y = x − có tập xác định D = ℝ\{0} nên hàm không thể đồng biến trên ℝ.
⇒ A sai.
Đáp án B hàm số y = 2x3 − x2 + 5x + 1 có tập xác định D = ℝ.
Xét đạo hàm có y' = 6x2 – 2x + 5 = 6 + > 0 ∀ x ∈ ℝ.
Vậy hàm số đồng biến trên ℝ ⇒ B đúng.
Đáp án C hàm số y = x4 + 2x2 − 3 có tập xác định D = ℝ.
Xét đạo hàm số có y'= 4x3 + 4x. Cho y'= 0 suy ra phương trình có nghiệm x = 0.
Vậy hàm số không thể đồng biến trên ℝ ⇒ C sai.
Đáp án D hàm số y = 2x2 + 3 có tập xác định D = ℝ.
Xét đạo hàm có y'= 4x. Cho y'= 0 suy ra phương trình có nghiệm x = 0.
Vậy hàm số không thể đồng biến trên ℝ⇒ D sai.
Bài 7 trang 11 SBT Toán 12 Tập 1: Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 4. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (−∞; 0).
B. (3; +∞).
C. (−1; 1).
D. (−∞; −1).
Lời giải:
Đáp án đúng là: D
Dựa vào đồ thị, ta thấy:
Hàm số đồng biến trên các khoảng (−1; 1) và (3; +∞).
Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; 3).
Bài 8 trang 11 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm trên ℝ và bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là:
A. 0.
B. 1.
C. 2.
D. 3.
Lời giải:
Đáp án đúng là: C
Căn cứ vào bảng xét dấu, ta thấy: y' = 0 tại 3 điểm x = −2; x = 1; x = 3. Tuy nhiên qua x = 1 thì y' không đổi dấu.
Vậy hàm số có 2 cực trị.
Bài 9 trang 12 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là:
A. −1.
B. 3.
C. 2.
D. 0.
Lời giải:
Đáp án đúng là: A
Từ bảng biến thiên, ta thấy hàm số đạt cực đại bằng 3 tại điểm x = −1.
Bài 10 trang 12 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x = −5.
B. Hàm số có giá trị cực đại bằng 0.
C. Hàm số đạt cực tiểu tại x = 2.
D. Hàm số đạt cực đại tại x = 4.
Lời giải:
Đáp án đúng là: C
Từ bảng biến thiên, ta có:
Hàm số đạt cực đại y = 4 tại x = 0.
Hàm số đạt cực tiểu y = −5 tại x = 2.
Bài 11 trang 12 SBT Toán 12 Tập 1: Cho hàm số f(x) có đạo hàm f'(x) = x2(x2 – 1)2(x – 2), ∀x ∈ ℝ. Số điểm cực trị của hàm số đã cho là:
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải:
Đáp án đúng là: A
Ta có: f'(x) = x2(x2 – 1)2(x – 2).
f'(x) = 0 ⇔ x2(x2 – 1)2(x – 2) = 0
⇔ x2(x − 1)2(x + 1)2(x – 2) = 0
⇔ x = 0 hoặc x = 1 hoặc x = −1 hoặc x = 2.
Tuy nhiên x = 0, x = 1, x = −1 là các nghiệm kép nên hàm số chỉ có 1 cực trị tại x = 2.
Bài 12 trang 12 SBT Toán 12 Tập 1: Cho hàm số y = 2x3 + 3x + 2. Kết luận nào sau đây đúng?
A. Hàm số có 3 cực trị.
B. Hàm số có 2 cực trị.
C. Hàm số có 1 cực trị.
D. Hàm số không có cực trị.
Lời giải:
Đáp án đúng là: D
Tập xác định: D = ℝ.
Ta có: y = 2x3 + 3x + 2 ⇒y' = 6x2 + 3.
Nhận thấy y' > 0 với ∀x ∈ ℝ.
Vậy hàm số không có cực trị.
Bài 13 trang 12 SBT Toán 12 Tập 1: Hàm số y = x3 – 3x2 – 9x – 3 đạt cực tiểu tại điểm:
A. −1.
B. 3.
C. 2.
D. −30.
Lời giải:
Đáp án đúng là: B
Tập xác định: D = ℝ.
Ta có: y = x3 – 3x2 – 9x – 3 ⇒ y' = 3x2 – 6x – 9.
y' = 0 khi x = 3 hoặc x = −1.
Ta có bảng biến thiên:
Vậy hàm số đạt cực tiểu tại điểm x = 3.
Bài 14 trang 12 SBT Toán 12 Tập 1: Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 5. Số điểm cực trị của hàm số đã cho là:
A. 2.
B. 4.
C. 1.
D. 3.
Lời giải:
Đáp án đúng là: B
Quan sát đồ thị, ta thấy hàm số có 4 điểm cực trị.
Bài 15 trang 13 SBT Toán 12 Tập 1: Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là:
A. 2.
B. 1.
C. −1.
D. 0.
Lời giải:
Đáp án đúng là: D
Quan sát đồ thị, ta thấy:
Giá trị cực tiểu của hàm số bằng 0 khi x = −1 và x = 3.
Giá trị cực đại của hàm số bằng 2 khi x = 1.
Bài 16 trang 13 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm trên ℝ và đồ thị hàm số y = f'(x) như Hình 7. Số điểm cực trị của hàm số y = f(x) là:
A. 4.
B. 3.
C. 2.
D. 1.
Lời giải:
Đáp án đúng là: D
Đồ thị trên là của hàm y = f'(x), nên ta có bảng biến thiên của hàm số y = f(x) như sau:
Vậy hàm số có 1 cực trị.
Bài 17 trang 13 SBT Toán 12 Tập 1: Cho hàm số y = x3 – 3x + 2.
|
a) y' = 3x2 – 3. |
|
|
|
b) y' = 0 khi x = −1, x = 1. |
|
|
|
c) y' > 0 khi x ∈ (−1; 1) và y' < 0 khi x ∈ (−∞; −1) ∪ (1; +∞). |
|
|
|
d) Giá trị cực đại của hàm số là fCĐ = 0. |
|
|
Lời giải:
|
a) Đ |
b) Đ |
c) S |
d) S |
Tập xác định: D = ℝ.
Ta có: y = x3 – 3x + 2 ⇒y' = 3x2 – 3.
y' = 0 ⇔ 3x2 – 3 = 0 ⇔ x = ±1.
Ta có bảng biến thiên như sau:
y' > 0 khi x ∈ (−∞; −1) và (1; +∞).
y' < 0 khi x ∈ (−1; 1).
Giá trị cực đại của hàm số là fCĐ = 4 khi x = −1.
Giá trị cực tiểu của hàm số là fCT = 0 khi x = 1.
Bài 18 trang 13 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm trên ℝ và đồ thị hàm số của y = f'(x) như Hình 8.
|
a) f'(x) = 0 khi x = 0, x = 1, x = 3. |
|
|
|
b) Hàm số y = f(x) đồng biến trên khoảng (−∞; 0). |
|
|
|
c) f'(x) > 0 khi x ∈ (0; 3). |
|
|
|
d) Hàm số y = f(x) đồng biến trên (0; 3). |
|
|
Lời giải:
|
a) Đ |
b) S |
c) S |
d) Đ |
Quan sát đồ thị hàm số y = f'(x), ta thấy f'(x) = 0 khi x = 0, x = 1, x = 3.
Ta có bảng biến thiên của hàm số y = f(x) như sau:
Tại x = 1, f'(x) = 0 nên f'(x) > 0 trên các khoảng (0; 1) và (1; 3).
Hàm số nghịch biến trên các khoảng (−∞; 0) và (3; +∞).
Hàm số đồng biến trên khoảng (0; 3).
Bài 19 trang 14 SBT Toán 12 Tập 1: Tìm các khoảng đơn điệu của mỗi hàm số sau:
a) y = -x3 + x2 + 3x – 1;
b) y = x3 – 3x2 + 3x – 1;
c) y = x4 + x2 – 2;
d) y = −x4 + 2x2 – 1;
e) ;
g) .
Lời giải:
a) y = -x3 + x2 + 3x – 1
Tập xác định: D = ℝ.
Ta có: y' = −x2 + 2x + 3.
y' = 0 ⇔ −x2 + 2x + 3 = 0 ⇔ x = 3 hoặc x = −1.
Ta có bảng xét dấu như sau:
Hàm số đồng biến trên khoảng (−1; 3).
Hàm số nghịch biến trên các khoảng (−∞; −1) và (3; +∞).
b) y = x3 – 3x2 + 3x – 1
Tập xác định: D = ℝ.
Ta có: y' = 3x2 – 6x + 3 = 3(x – 1)2 ≥ 0, ∀x ∈ ℝ.
Vậy hàm số đồng biến trên ℝ.
c) y = x4 + x2 – 2
Tập xác định: D = ℝ.
Ta có: y' = 4x3 + 2x = 2x(2x2 + 1);y' = 0 khi x = 0.
Ta có bảng biến thiên:
Vậy hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (−∞; 0).
d) y = −x4 + 2x2 – 1
Tập xác định: D = ℝ.
Ta có: y' = −4x3 + 4x = 4x.(−x2 + 1).
y' = 0 khi x = 0 hoặc x = ±1.
Ta có bảng biến thiên như sau:
Vậy hàm số đồng biến trên các khoảng (−∞; −1) và (0; 1).
Hàm số nghịch biến trên các khoảng (−1; 0) và (1; +∞).
e)
Tập xác định: D = ℝ\{4}.
Ta có < 0, ∀x ∈ D.
Vậy hàm số nghịch biến trên các khoảng (−∞; 4) và (4; +∞).
g)
Tập xác định: D = ℝ\{−2}.
Ta có: .
y' = 0 khi x = 0 hoặc x = −4.
Ta có bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng (−∞; −4) và (0; +∞).
Hàm số nghịch biến trên các khoảng (−4; −2) và (−2; 0).
Bài 20 trang 14 SBT Toán 12 Tập 1: Tìm điểm cực trị của mỗi hàm số sau:
a) y = x3 – 12x + 8;
b) y = 2x4 – 4x2 – 1;
c) ;
d) y = −x + 1 − .
Lời giải:
a) y = x3 – 12x + 8
Tập xác định: D = ℝ.
Ta có: y' = 3x2 – 12.
y' = 0 khi x = ± 2.
Ta có bảng biến thiên:
Vậy hàm số có điểm cực đại x = −2, điểm cực tiểu x = 2.
b) y = 2x4 – 4x2 – 1
Tập xác định: D = ℝ.
Ta có y' = 8x3 – 8x.
y' = 0 khi x = 0 hoặc x = ±1.
Ta có bảng biến thiên sau:
Hàm đạt cực đại tại điểm x = 0; hàm đạt cực tiểu tại điểm x = −1 và x = 1.
c)
Tập xác định: D = ℝ\ {−1}.
Ta có: = .
y' = 0 khi x = 0 hoặc x = −2.
Ta có bảng biến thiên:
Hàm số đạt cực đại x = −2 và hàm số đạt cực tiểu tại x = 0.
d) y = −x + 1 −
Tập xác định: D = ℝ\{2}.
Ta có: .
y' = 0 khi x = 5 hoặc x = −1.
Ta có bảng biến thiên:
Vậy hàm số đạt cực đại tại x = 5 và đạt cực tiểu tại x = −1.
Bài 21 trang 14 SBT Toán 12 Tập 1: Dùng đạo hàm của hàm số, hãy giải thích:
a) Hàm số y = ax đồng biến trên ℝ khi a > 1, nghịch biến trên ℝ khi 0 < a < 1.
b) Hàm số y = loga x đồng biến trên khoảng (0; +∞) khi a > 1, nghịch biến trên khoảng (0; +∞) khi 0 < a < 1.
Lời giải:
a)
Tập xác định: D = ℝ.
Ta có: y = ax ⇒y' = ax.lna.
Với a > 1 thì lna > 0 nên y' > 0 với mọi x ∈ ℝ. Vậy a > 1 thì hàm số y = ax đồng biến trên ℝ.
Với 0 < a < 1 thì lna < 0 nên y' < 0 với mọi x ∈ ℝ. Vậy 0 < a < 1 thì hàm số y = ax nghịch biến trên ℝ.
b) Tập xác định: D = (0; +∞).
Ta có: y = loga x ⇒ .
Với a > 1 ta có lna > 0 suy ra > 0 ∀x ∈ (0; +∞). Vậy hàm số y = loga x đồng biến trên khoảng (0; +∞).
Với 0 < a < 1 ta có lna < 0 suy ra < 0 ∀x ∈ (0; +∞). Vậy hàm số nghịch biến trên khoảng (0; +∞).
Bài 22 trang 14 SBT Toán 12 Tập 1: Chứng minh rằng:
a) Hàm số nghịch biến trên khoảng (−∞; −2) và đồng biến trên khoảng (2; +∞).
b) Hàm số y = ln(x2 + 1) nghịch biến trên khoảng (−∞; 0) và đồng biến trên khoảng (0; +∞).
c) Hàm số đồng biến trên khoảng (−∞; 1) và nghịch biến trên khoảng (1; +∞).
Lời giải:
a) Tập xác định: D = (−∞; −2] ∪ [2; +∞).
Ta có: ⇒ .
y' = 0 khi x = 0 (loại do x = 0 không thuộc TXĐ).
Ta có bảng biến thiên:
Từ bảng biến thiên, suy ra hàm số nghịch biến trên khoảng (−∞; −2) và đồng biến trên khoảng (2; +∞).
b) Tập xác định: D = ℝ.
Ta có: .
y' = 0 khi x = 0.
Ta có bảng biến thiên:
Từ bảng biến thiên, ta có hàm số y = ln(x2 + 1) nghịch biến trên khoảng (−∞; 0) và đồng biến trên khoảng (0; +∞).
c) Tập xác định: D = ℝ.
Ta có: ⇒y' = (−2x + 2) . . ln2.
y' = 0 khi x = 1.
Ta có bảng xét dấu như sau:
Hàm số đồng biến trên khoảng (−∞; 1) và nghịch biến trên khoảng (1; +∞).
Bài 23 trang 14 SBT Toán 12 Tập 1: Tìm điểm cực trị của mỗi hàm số sau:
a) y = x.ex;
b) y = (x + 1)2.e-x;
c) y = x2.ln x;
d) .
Lời giải:
a) Tập xác định: D = ℝ.
Ta có: y = x.ex ⇒ y' = (1 + x).ex.
y' = 0 khi x = −1.
Ta có bảng biến thiên:
Vậy hàm số đạt cực tiểu tại x = −1, hàm số không có cực đại.
b) Tập xác định: D = ℝ.
Ta có: y = (x + 1)2.e-x ⇒y' = 2(x + 1)e-x – (x + 1)2e-x = (1 – x)(x + 1)e-x.
y' = 0 khi x = ±1.
Ta có bảng biến thiên:
Vậy hàm số đạt cực đại tại x = 1 và đạt cực tiểu tại x = −1.
c) Tập xác định: D = (0; +∞).
Ta có: y = x2.ln x ⇒y' = 2x.lnx + x = x(2lnx + 1).
y' = 0 khi x = .
Ta có bảng biến thiên như sau:
Vậy hàm số đạt cực tiểu tại x = , hàm số không có cực đại.
d) Tập xác định: D = (0; +∞).
Ta có: ⇒ .
y' = 0 khi x = e.
Ta có bảng biến thiên:
Vậy hàm đạt cực tiểu tại x = e, hàm số không có cực đại.
Bài 24 trang 14 SBT Toán 12 Tập 1: Trong một thí nghiệm y học, người ta cấy 1 000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức:
N(t) = ,
trong đó t là thời gian tính bằng giây (t ≥ 0) (Nguồn R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Trong khoảng thời gian nào từ lúc nuôi cấy, lượng vi khuẩn sẽ tăng lên?
Lời giải:
Ta có: N(t) = N(t) = .
.
N'(t) = 0 khi t = 10.
Ta có bảng biến thiên:
Từ bảng biến thiên, ta thấy trong khoảng thời gian từ (0; 10) giây, tức là 10 giây đầu thì lượng vi khuẩn sẽ tăng lên.
Bài 25 trang 15 SBT Toán 12 Tập 1: Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình
s(t) = t3 – 6t2 + 14t + 1,
trong đó t tính bằng giây và s tính bằng mét. Trong khoảng thời gian nào của 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên?
Lời giải:
Ta có: s(t) = t3 – 6t2 + 14t + 1⇒v(t) = s'(t) = 3t2 – 12t + 14.
v(t) = 3t2 – 12t + 14, ∀t ≥ 0.
Xét v'(t) = 6t – 12.
v'(t) = 0 khi t = 2.
Ta có bảng xét dấu của v'(t):
Vận tốc tức thời của chất điểm tăng lên trong khoảng thời gian từ 2 giây đến 5 giây.
Lý thuyết Tính đơn điệu và cực trị của hàm số
1. Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
Định lý 1
|
Cho hàm số y = f(x) có đạo hàm trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng - Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K - Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K |
Ví dụ: Hàm số y = |x| đồng biến trên khoảng , nghịch biến trên khoảng
Định lý 2
|
Cho hàm số y = f(x) có đạo hàm trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu f’(x) 0 (hoặc f’(x) 0) với mọi x thuộc K và f’(x) = 0 chỉ tại một số hữa hạn điểm của K thì hàm số f(x) đồng biến (hoặc nghịch biến) trên K |
Ví dụ: Hàm số có y’ = 2x – 4
y’ > 0 với nên HS đồng biến trên khoảng
y’ < 0 với nên HS đồng biến trên khoảng
2. Điểm cực trị, giá trị cực trị của hàm số
Khái niệm cực trị của hàm số
|
Cho hàm số y = f(x) liên tục trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng và - được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm sao cho (a;b) K và với mọi và . Khi đó, được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là - được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm sao cho (c;d) K và với mọi và . Khi đó, được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) |
Ví dụ: Cho đồ thị của hàm số y = f(x) như sau
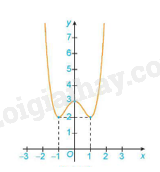
Hàm số đạt cực tiểu tại x = -1 và = y(-1) = 2
Hàm số đạt cực đại tại x = 0 và = y(0) = 3
Hàm số đạt cực tiểu tại x = 1 và = y(1) = 2
Định lý
|
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm và có đạo hàm trên các khoảng và . Khi đó: a) Nếu f’(x) < 0 với mọi và f’(x) > 0 với mọi thì hàm số f(x) đạt cực tiểu tại điểm b) Nếu f’(x) > 0 với mọi và f’(x) < 0 với mọi thì hàm số f(x) đạt cực tiểu tại điểm |
Ví dụ: Tìm cực trị của hàm số .
Tập xác định của hàm số là R.
Ta có: ; y’ = 0 x = 1 hoặc x = 3.
BBT:
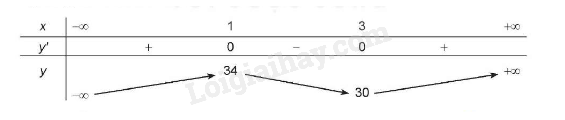
Hàm số đạt cực đại tại x = 1 và = y(1) = 34
Hàm số đạt cực tiểu tại x = 3 và = y(3) = 30
Xem thêm các bài giải SBT Toán lớp 12 Cánh diều hay, chi tiết khác:
Bài 1: Tính đơn điệu của hàm số
Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 3: Đường tiệm cận của đồ thị hàm số