Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng

Van Anh Ngày: 18-09-2024 Lớp 7

292

Tailieumoi.vn xin giới thiệu Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết trực tâm của tam giác. Mời các bạn đón xem:

Tính chất trực tâm của tam giác

A. Lý thuyết trực tâm của tam giác

1. Định nghĩa trực tâm của tam giác

Trực tâm của một tam giác là một điểm đặc biệt và quan trọng trong tam giác, vì nó có một số tính chất đặc biệt. Trực tâm là điểm giao của ba đường cao, nghĩa là các đường thẳng từ mỗi đỉnh của tam giác đến đối diện của nó sao cho tạo thành một góc vuông. Việc xác định trực tâm của tam giác có thể được thực hiện bằng cách kẻ hai đường cao của tam giác đến hai cạnh đối diện. Hai đường cao này sẽ giao nhau tại trực tâm của tam giác. Điểm này cũng là tâm của đường tròn ngoại tiếp tam giác, tức là đường tròn lớn nhất mà có thể vẽ được qua ba đỉnh của tam giác.

Trực tâm của tam giác có một số tính chất đáng chú ý. Ví dụ, trong tam giác cân, trực tâm cũng là tâm của đường tròn nội tiếp và là trung điểm của cạnh đáy. Trong tam giác vuông, trực tâm nằm trên cạnh huyền và chính giữa hai đỉnh vuông góc. Trực tâm của tam giác cũng có tính chất là điểm duy nhất trong tam giác mà tổng khoảng cách từ trực tâm đến các đỉnh là nhỏ nhất. Trực tâm của tam giác không chỉ có ý nghĩa hình học mà còn được áp dụng trong các bài toán và bằng chứng liên quan đến tam giác. Hiểu rõ về trực tâm giúp chúng ta nắm bắt và áp dụng các tính chất của tam giác một cách hiệu quả trong giải toán và nghiên cứu hình học.

2. Định nghĩa đường cao

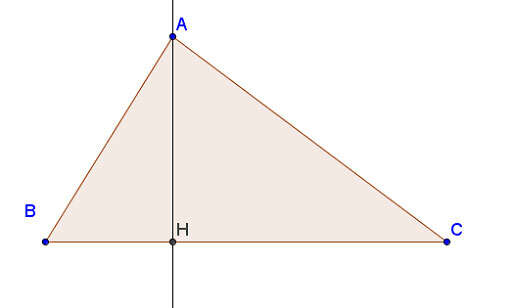
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 1)

Đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện được gọi là đường cao của tam giác đó, và mỗi tam giác sẽ có ba đường cao.

3. Tính chất trực tâm của tam giác

Trực tâm của tam giác là một điểm đặc biệt trong tam giác và có một số tính chất như sau:

- Tính chất 1: Trực tâm là điểm trùng điểm giao của ba đường thẳng đồng trung và đồng quy trong tam giác, bao gồm:

+ Đường trung trực: Đường thẳng đi qua trực tâm và đỉnh tương ứng của cạnh.

+ Đường phân giác: Đường thẳng chia một góc trong tam giác thành hai phần bằng nhau, kết hợp với trực tâm.

+ Đường cao: Đường thẳng từ một đỉnh của tam giác vuông góc với cạnh đối diện, cắt nhau tại trực tâm.

- Tính chất 2: Trực tâm cắt đường trung trực của hai cạnh thành hai đoạn có độ dài bằng nhau. Điều này có nghĩa là trực tâm cách các đỉnh của tam giác một khoảng bằng nhau.

- Tính chất 3: Trực tâm là tâm của đường tròn ngoại tiếp của tam giác, nghĩa là nếu ta vẽ một đường tròn đi qua ba đỉnh của tam giác, trực tâm sẽ nằm trên đường tròn đó và là tâm của nó.

- Tính chất 4: Trực tâm của tam giác nhọn nằm bên trong tam giác, trong khi trực tâm của tam giác tù nằm bên ngoài tam giác.

- Tính chất 5: Trực tâm của tam giác vuông nằm trên cạnh huyền và chính giữa hai đỉnh vuông góc của tam giác.

- Tính chất 6: Trực tâm là điểm duy nhất trong tam giác mà nếu ta vẽ các đường từ trực tâm đến các đỉnh của tam giác, tổng độ dài các đường đó là nhỏ nhất. Điều này có nghĩa là trực tâm nằm gần nhất với các đỉnh của tam giác so với bất kỳ điểm nào khác.

- Tính chất 7: Trực tâm cũng là tâm của đường tròn ngoại tiếp của tam giác, tức là đường tròn lớn nhất mà có thể vẽ được qua ba đỉnh của tam giác.

=> Trực tâm của tam giác có vai trò quan trọng trong việc xác định các đường thẳng và đường tròn liên quan đến tam giác, cũng như các tính chất đặc biệt của tam giác. Nó được sử dụng trong các bằng chứng và bài toán liên quan đến tam giác và hình học tam giác.

4. Cách xác định trực tâm của tam giác

a. Trực tâm của tam giác nhọn

Đầu tiên, kẻ hai đường cao từ hai đỉnh của tam giác về hai cạnh đối diện. Đường cao là đoạn thẳng vuông góc với cạnh tương ứng và đi qua đỉnh không nằm trên cạnh đó. Hai đường cao này sẽ cắt nhau tại một điểm duy nhất, đó chính là trực tâm của tam giác. Trực tâm nằm trong miền của tam giác nhọn và có vị trí gần trung điểm của các cạnh.

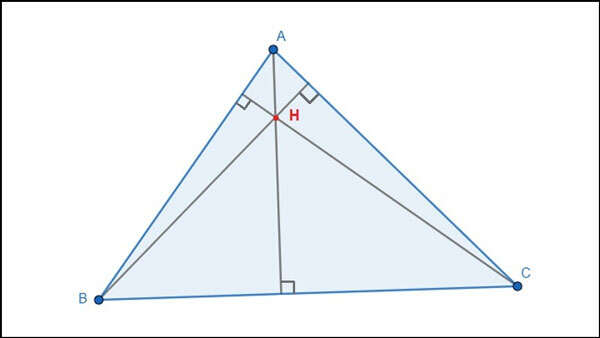
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 2)

Tam giác nhọn ABC có trực tâm H nằm ở miền trong tam giác.

b. Trực tâm của tam giác vuông

Trực tâm của tam giác vuông trùng với đỉnh của góc vuông. Điều này xuất phát từ việc hai cạnh tạo thành góc vuông cũng chính là đường cao của tam giác. Do đó, ta không cần kẻ thêm đường cao hay tìm giao điểm nào khác, trực tâm chính là đỉnh góc vuông.

Ví dụ: Tam giác vuông EFG có trực tâm H trùng với góc vuông E.

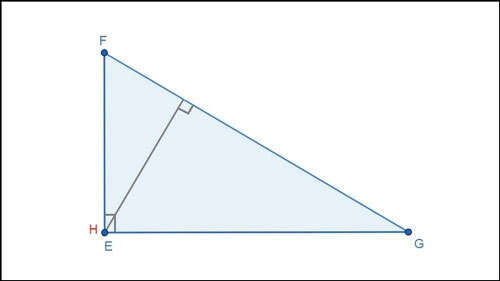
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 3)

c. Trực tâm của tam giác tù

Tương tự như tam giác nhọn, ta kẻ hai đường cao từ hai đỉnh của tam giác về hai cạnh đối diện. Tuy nhiên, trực tâm của tam giác tù nằm ở bên ngoài tam giác. Để xác định trực tâm, ta cần vẽ thêm một đường cao từ điểm đỉnh góc tù xuống cạnh đối diện. Đường cao này cắt đường cao khác tại một điểm, đó chính là trực tâm của tam giác tù. Trực tâm nằm ở ngoài miền tam giác và nằm gần trung điểm của đoạn thẳng nối hai điểm chân của hai đường cao cắt nhau.

Trực tâm của tam giác tù nằm ở miền ngoài tam giác đó.

Ví dụ: Tam giác tù BCD có trực tâm H nằm ở miền ngoài tam giác

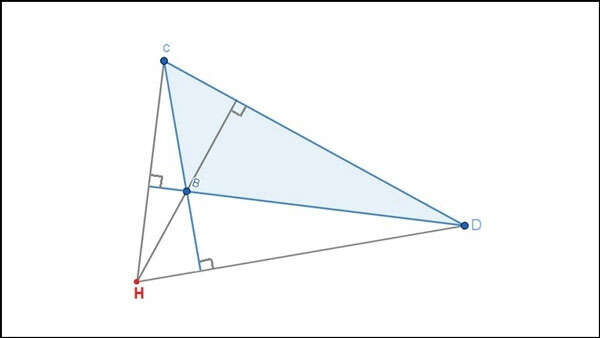
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 4)

5. Ứng dụng trực tâm của tam giác

Trực tâm trong tam giác có nhiều ứng dụng quan trọng và hữu ích trong lĩnh vực hình học và các ngành khoa học khác. Dưới đây là một số ứng dụng của trực tâm trong tam giác:

- Trực tâm là tâm trong đường tròn ngoại tiếp tam giác: Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Trực tâm là tâm của đường tròn ngoại tiếp, nghĩa là khoảng cách từ trực tâm đến mỗi đỉnh của tam giác là bằng nhau.

- Trực tâm là tâm trong đường tròn nội tiếp tam giác: Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với các cạnh của tam giác. Trực tâm là tâm của đường tròn nội tiếp, nghĩa là các đoạn thẳng nối từ trực tâm đến các điểm tiếp xúc cạnh là vuông góc với cạnh tương ứng.

- Trực tâm là tâm trong đường tròn nội tiếp nửa ngoại tiếp tam giác: Đường tròn nội tiếp nửa ngoại tiếp tam giác là đường tròn tiếp xúc với một cạnh và tiếp xúc tiếp với phần còn lại của cạnh kế tiếp. Trực tâm là tâm của đường tròn nội tiếp nửa ngoại tiếp.

- Trực tâm là trung điểm của các đoạn thẳng nối từ trực tâm đến các đỉnh của tam giác: Điều này có nghĩa là trực tâm chia đôi các đoạn thẳng nối từ trực tâm đến các đỉnh của tam giác.

- Trực tâm là giao điểm của ba đường cao của tam giác: Đường cao là đoạn thẳng vuông góc với cạnh tương ứng và đi qua đỉnh không nằm trên cạnh đó. Trực tâm là điểm giao của ba đường cao của tam giác.

- Trực tâm giúp xác định các thuộc tính và vị trí của tam giác: Nhờ trực tâm, ta có thể dễ dàng xác định được tâm của đường tròn ngoại tiếp, đường tròn nội tiếp, tính chất đối xứng và cân của tam giác.

- Trực tâm có thể được sử dụng để tính toán các giá trị hình học khác như diện tích tam giác, khoảng cách từ trực tâm đến các điểm khác trong tam giác, và các thuộc tính khác của tam giác.

=> Tóm lại, trực tâm là một điểm quan trọng và có nhiều ứng dụng trong tam giác. Việc hiểu và sử dụng trực tâm giúp ta nắm bắt và áp dụng các tính chất và quy luật hình học trong tam giác một cách hiệu quả.

B. Bài tập trực tâm của tam giác

1. Bài tập trắc nghiệm

Câu 1.

Cho đoạn thẳng AB và điểm M nằm giữa A và B (MA < MB). Vẽ tia Mx vuông góc với AB, trên đó lấy hai điểm C và D sao cho MA = MC, MD = MB.
Tia AC cắt BD ở E. Tính số đo góc

A. 30⁰B. 45⁰C. 60⁰D. 90⁰

Đáp án: D

Câu 2

Cho ΔABC cân tại A, hai đường cao BD và CE cắt nhau tại I. Tia AI cắt BC tại M. Khi đó ΔMED là tam giác gì?

A. Tam giác cân
B. Tam giác vuông cân
C. Tam giác vuông
D. Tam giác đều.

Đáp án: A

Câu 3. Cho ΔABC vuông tại A, trên cạnh AC lấy các điểm D, E sao cho = = . Trên tia đối của tia DB lấy điểm F sao cho DF = BC. Tam giác CDF là tam giác gì?

A. Tam giác cân tại F
B. Tam giác vuông tại D
C. Tam giác cân tại D
D. Tam giác cân tại C

Đáp án: A

Bài 3: Cho ΔABC, hai đường cao BD và CE. Gọi M là trung điểm của BC. Em hãy chọn câu sai:

A. BM = MC
B. ME = MD
C. DM = MB
D. M không thuộc đường trung trực của DE

Giải

Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 5)

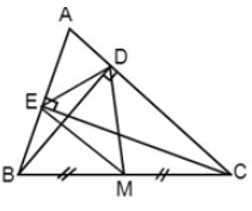
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 6)

Vì M là trung điểm của BC (gt) suy ra BM = MC (tính chất trung điểm), loại đáp án A.

Xét ΔBCE có M là trung điểm của BC (gt) suy ra EM là trung tuyến

⇒ EM = BC/2 (1) (trong tam giác vuông đường trung tuyến ứng cới cạnh huyền bằng nửa cạnh ấy)

Xét ΔBCD có M là trung điểm của BC (gt) suy ra DM là trung tuyến

⇒ DM = MB = BC/2 (2) (trong tam giác vuông đường trung tuyến ứng cới cạnh huyền bằng nửa cạnh ấy) nên loại đáp án C

Từ (1) và (2) ⇒ EM = DM ⇒ M thuộc đường trung trực của DE. Loại đáp án B, chọn đáp án D

Chọn đáp án D

Bài 4: Cho ΔABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE và AC cắt nhau tại O. Chọn câu đúng

A. ΔABO = ΔCOE
B. ΔBOA = ΔCOE
C. ΔAOB = ΔCOE
D. ΔABO = ΔCEO

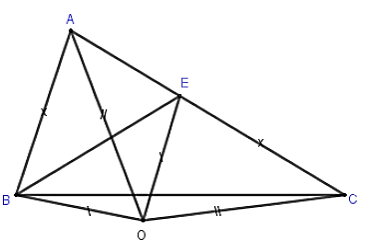
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 8)

Xét tam giác ΔAOB và ΔCOE có

+ OA = OC (vì O thuộc đường trung trực của AC )

+ OB = OE (vì O thuộc đường trung trực của BE )

+ AB = CE (giả thiết)

Do đó ΔAOB = ΔCOE (c-c-c)

Chọn đáp án C

2. Bài tập tự luận

Bài 1

Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.

Lời giải

+ Xét ΔABC vuông tại A

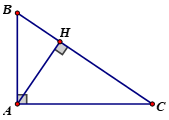
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 9)

AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB

hay AB, AC là hai đường cao của tam giác ABC.

Mà AB cắt AC tại A

⇒ A là trực tâm của tam giác vuông ABC.

Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông

+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.

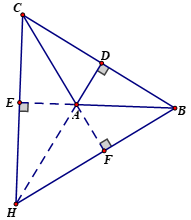
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 10)

+ Giả sử E nằm giữa A và B, khi đó

$\begin{aligned} &\widehat{\mathrm{CAE}} \equiv \widehat{\mathrm{CAB}} \text { là góc tù. }\\ &\text { Trong } \triangle \mathrm{ACE} \text { có }\\ &\widehat{\mathrm{CAE}}+\widehat{\mathrm{ACE}}+\widehat{\mathrm{CEA}}>90^{\circ}+\widehat{\mathrm{ACE}}+90^{\circ}\\ &=180^{\circ}+\widehat{\mathrm{ACE}}>180^{\circ} \end{aligned}$

Vậy E nằm ngoài A và B

⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.

+ Tương tự ta có tia BF nằm bên ngoài ΔABC.

+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.

Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.

Bài 2: Cho hình vẽ

a) Chứng minh NS ⊥ LM

b) Khi góc LNP = 50^o, hãy tính góc MSP và góc PSQ.

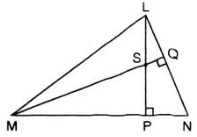
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 12)

Lời giải

a) Trong ΔMNL có:

LP ⊥ MN nên LP là đường cao của ΔMNL.

MQ ⊥ NL nên MQ là đường cao của ΔMNL.

Mà LP, MQ cắt nhau tại điểm S

Nên: theo tính chất ba đường cao của một tam giác, S là trực tâm của tam giác.

⇒ đường thẳng SN là đường cao của ΔMNL.

hay SN ⊥ ML.

+ Ta có : trong tam giác vuông, hai góc nhọn phụ nhau nên :

ΔNMQ vuông tại Q có:

$\begin{aligned} &\mathrm{LNP}+\widehat{\mathrm{QMN}}=90^{\circ} \Rightarrow \widehat{\mathrm{LNP}}=90^{\circ}-\widehat{\mathrm{QMN}}\\ &\Delta \text { MPS vuông tại } \mathrm{P} \text { có }\\ &\widehat{\mathrm{QMN}}+\overrightarrow{\mathrm{MSP}}=90^{\circ} \Rightarrow \widehat{\mathrm{MSP}}=90^{\circ}-\widehat{\mathrm{QMP}}\\ &\Rightarrow \widehat{\mathrm{LNP}}=\widehat{\mathrm{MSP}} . \text { Mà } \widehat{\mathrm{LNP}}=50^{\circ}(\mathrm{gt})\\ &\Rightarrow \widehat{\mathrm{MSP}}=50^{\circ}\\ &+\overline{\mathrm{MSP}}+\mathrm{PSQ}=180^{\circ} \text &\Rightarrow \widehat{\mathrm{PSQ}}=180^{\circ}-\overline{\mathrm{MSP}}=180^{0}-50^{0}=130^{\circ} \end{aligned}$

Bài 3:

Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K).

Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.

Chứng minh KN ⊥ IM.

Lời giải

Vẽ hình minh họa:

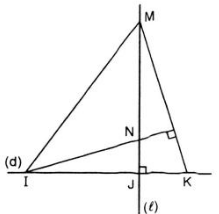
Tính chất trực tâm của tam giác: Lý thuyết và 20 bài tập vận dụng (ảnh 16)

Trong một tam giác, ba đường cao đồng quy tại một điểm là trực tâm của tam giác đó.

l ⊥ d tại J, và M, J ∈ l ⇒ MJ ⟘ IK ⇒ MJ là đường cao của ΔMKI.

N nằm trên đường thẳng qua I và vuông góc với MK ⇒ IN ⟘ MK ⇒ IN là đường cao của ΔMKI.

IN và MJ cắt nhau tại N .

Theo tính chất ba đường cao của ta giác ⇒ N là trực tâm của ΔMKI.

⇒ KN cũng là đường cao của ΔMKI ⇒ KN ⟘ MI.

Vậy KN ⏊ IM

3. Bài tập tự luyện

Bài 1: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ta trực tâm của tam giác đó.

Bài 2: Cho đường tròn (O, R) , gọi BC là dây cung cố định của đường tròn và A là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác ABC.

Bài 3: Cho △ABC có các đường cao AD;BE;CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.

a) Chứng minh: IJ ⊥ EF

b) Chứng minh: IE ⊥ JE

Bài 4: Cho △ABC có các đường cao AD;BE;CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.

a) Chứng minh: JT⊥EFJT⊥EF

b) Chứng minh: IE⊥JEIE⊥JE

c) Chứng minh: DA là tia phân giác của góc EDF.

d) Gọi P;Q là hai điểm đối xứng của D qua AB và AC

Chứng minh: P;F;E;Q thẳng hàng.

Bài 5: Cho tam giác ABC với trực tâm H. Chứng minh rằng các điểm đối xứng với H qua các đường thẳng chứa các cạnh hay trung điểm của các cạnh nằm trên đường tròn (ABC).

Bài 6: Cho tam giác ABC với các đường cao AD, BE, CF. Trực tâm H.DF cắt BH tại M, DE cắt CH tại N. chứng minh đường thẳng đi qua A và vuông góc với MN đi qua tâm ngoại tiếp của tam giác HBC.

Bài 7: Cho tứ giác lồi ABCD có 3 góc ở các đỉnh A, B và C bằng nhau. Gọi H và O lần lượt là trực tâm và tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh rằng O, H, D thẳng hàng.