Tailieumoi.vn xin giới thiệu 3 Dạng bài tập về phương trình bậc hai một ẩn lớp 9 hay, chọn lọc được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết phương trình bậc hai một ẩn lớp 9. Mời các bạn đón xem:

3 Dạng bài tập về phương trình bậc hai một ẩn

A. 3 dạng bài tập về phương trình bậc hai một ẩn

Dạng 1.1: Giải phương trình: ax² + bx + c = 0 (a ≠ 0)

Bước 1: Xác định các hệ số a; b; c (hoặc a; b'; c) của phương trình bậc hai ax² + bx + c.

Bước 2: Tính Δ = b² - 4ac (hoặc Δ' = b'² - ac ).

+ TH1: Δ < 0, phương trình vô nghiệm.

+ TH2: Δ = 0, phương trình có nghiệm kép 

+ TH3: Δ > 0, phương trình có hai nghiệm phân biệt 

Bước 3: Tìm nghiệm của phương trình (nếu có).

Bước 4: Kết luận.

Dạng 1.2: Kiểm tra một giá trị x₀ có là nghiệm của phương trình: ax² + bx + c = 0 (a ≠ 0) hay không.

Bước 1: Thay giá trị x₀ vào vế trái của phương trình: ax₀ + bx₀ + c

Bước 2: Kết luận.Tính vế trái. Nếu kết quả bằng 0 thì x₀ là một nghiệm của phương trình.

Bước 3: Kết luận.

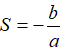
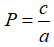
Định lý Vi-ét: Nếu phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ (phân biệt hoặc trùng nhau) thì tổng các nghiệm  và tích các nghiệm .

Dạng 2.1: Tìm tham số m để phương trình có nghiệm thỏa mãn điều kiện cho trước

Bước 1: Tìm điều kiện để phương trình có nghiệm.

Bước 2: Tính tổng S và tích P của hai nghiệm theo định lý Vi-ét.

Bước 3: Sử dụng hệ thức Vi-ét, kết hợp biến đổi đẳng thức, bất đẳng thức để tìm tham số.

Bước 4: Đối chiếu điều kiện và kết luận.

Dạng 2.2: Tìm tham số và tìm nghiệm còn lại khi biết trước một nghiệm x₀ của phương trình.

Bước 1: Thay giá trị x₀ vào phương trình để tìm tham số.

Bước 2: Thay giá trị của tham số hệ thức Vi-ét để tìm nghiệm còn lại.

Bước 3: Kết luận.

Dạng 2.3: Khi phương trình bậc hai có nghiệm, tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số.

Bước 1: Tìm điều kiện để phương trình có nghiệm.

Bước 2: Tính tổng S và tích P của hai nghiệm theo định lý Vi-ét.

Bước 3: Tính m theo S và P.

Bước 4: Khử m và tìm ra hệ thức.

Bước 5: Kết luận.

Dạng 2.4. Áp dụng hệ thức Vi-ét để tính nhẩm nghiệm của phương trình bậc hai

Cho phương trình bậc hai ax² + bx + c = 0 (a ≠ 0).

+) Nếu a + b + c = 0 thì phương trình có nghiệm x₁ = 1 và x₂ = .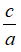

+) Nếu a - b + c = 0 thì phương trình có nghiệm x₁ = -1 và x₂ = .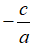

Dạng 2.5. Tìm hai số khi biết tổng và tích

Nếu hai số u và v có tổng u + v = S và tích u.v = P thì hai số đó là nghiệm của phương trình x² - Sx + P = 0 .

Điều kiện để có u và v là S² - 4P ≥ 0.

Dạng 3.1: Giải và biện luận phương trình theo tham số m

Bước 1: Xác định các hệ số a; b; c (hoặc a; b'; c).

Bước 2: Giải phương trình theo m:

+) Với giá trị của m mà a = 0, giải phương trình bậc nhất.

+) Với giá trị của m mà a ≠ 0, giải phương trình bậc hai: Tính Δ = b'² - ac (hoặc Δ' = b² - 4ac), xét các trường hợp của Δ chứa tham số và tìm nghiệm theo tham số.

Bước 3: Kết luận.

Biện luận phương trình:

- Phương trình có nghiệm khi:

+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.

+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm.

- Phương trình có một nghiệm khi:

+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.

+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm kép.

- Phương trình có hai nghiệm phân biệt khi: Giá trị của m mà a ≠ 0, phương trình bậc hai có hai nghiệm phân biệt.

Dạng 3.2: Xác định dấu các nghiệm của phương trình

Bước 1: Xác định hệ số.

Bước 2: Tính Δ = b² - 4ac (hoặc Δ' = b² - 4ac) để kiểm tra phương trình có nghiệm hay không.

Bước 3: Trong trường hợp phương trình có nghiệm (Δ ≥ 0 hoặc Δ' ≥ 0), tính tổng S và tích P của hai nghiệm theo định lý Vi-ét để xét dấu các nghiệm của phương trình.

+) Phương trình có hai nghiệm cùng dấu: P > 0.

+) Phương trình có hai nghiệm dương: .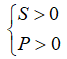

+) Phương trình có hai nghiệm âm: .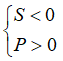

+) Phương trình có hai nghiệm trái dấu: P < 0.

Chú ý: Phương trình có hai nghiệm trái dấu chỉ cần xét P < 0 hoặc a.c < 0.

Bước 4: Kết luận.

Dạng 3.3: Tìm m để phương trình có nghiệm thỏa mãn điều kiện cho trước

Dạng 3.3.1: Tìm m để phương trình có nghiệm thỏa mãn điều kiện về dấu hoặc thỏa mãn đẳng thức, bất đẳng thức liên hệ giữa các nghiệm

Bước 1: Tìm điều kiện a ≠ 0 (nếu cần) và điều kiện để phương trình có nghiệm.

Bước 2: Tính tổng S và tích P của hai nghiệm theo định lý Vi-ét.

Bước 3: Sử dụng hệ thức Vi-ét, kết hợp biến đổi đẳng thức, bất đẳng thức để tìm tham số.

Bước 4: Đối chiếu điều kiện và kết luận.

Dạng 3.3.2: Tìm tham số m để phương trình có một nghiệm là x₀.

Bước 1: Thay giá trị x₀ vào phương trình để tìm tham số.

Bước 2: Thay giá trị của tham số vào phương trình hoặc hệ thức Vi-ét để tìm nghiệm còn lại.

Bước 3: Kết luận.

Dạng 3.3.3: Tìm giá trị của tham số để hai phương trình có ít nhất một nghiệm chung.

Bước 1: Tìm điều kiện để các phương trình có nghiệm.

Bước 2: Tìm nghiệm chung và tìm tham số: Có thể giả sử x₀ là nghiệm chung, lập hệ phương trình trình hai ẩn (x₀ và tham số) và giải hệ phương trình.

Bước 3: So sánh với điều kiện và kết luận.

B. Bài tập về phương trình bậc hai một ẩn

1. Bài tập trắc nghiệm

Bài 1: Tập nghiệm của phương trình x² + 3x - 1 = 0 là:

Lời giải

Chọn C

Bài 2: Giá trị nào sau đây là nghiệm của phương trình 3x² + 7x + 2 = 0

Lời giải

Chọn B

Bài 3: Phương trình x² - 2mx + m = 0 với m = 1 có tập nghiệm là:

Lời giải

Chọn C

Bài 4: Cho phương trình bậc hai (m - 1)x² - 2mx + m + 1 = 0 (m là tham số). Các giá trị nguyên của m để phương trình có nghiệm nguyên là:

Lời giải

Chọn A

Bài 5: Phương trình x² + (2m + 1)x + 3m = 0 (với m là tham số) có hai nghiệm phân biệt, trong đó có một nghiệm là x₁ = 3, nghiệm còn lại là x₂ bằng:

Lời giải

Chọn D

Bài 6: Tìm hệ thức liên hệ giữa hai nghiệm của phương trình x² - (m + 3)x + 2m - 5 = 0 không phụ thuộc vào m.

Lời giải

Chọn A

Bài 7: Cho phương trình x² - 2x - 8 = 0 có hai nghiệm x₁ và x₂. Phương trình bậc hai một ẩn có hai nghiệm là y₁ = x₁ - 3 và y₂ = x₂ - 3 là:

Lời giải

Chọn C

Bài 8: Giải phương trình x² - 2x + 1 - m² = 0 với m là tham số, m ≠ 0.

Lời giải

Chọn A

Bài 9: Cho phương trình x² + √7x + 1 = 0. Khẳng định nào sau đây là đúng?

Lời giải

Chọn B

Bài 10: Số các giá trị nguyên của tham số m để phương trình x² - 2x + m = 0 có hai nghiệm phân biệt x₁; x₂ sao cho x₁².x₂² ≤ 4 là:.

Lời giải

Chọn B

Bài 11: Phương trình bậc hai mx² + (2m + 1)x + 3 = 0 có một nghiệm là x = -1. Giá trị của m và nghiệm còn lại là:

Lời giải

Chọn A

Bài 12: Cho hai phương trình bậc hai x² + 2x + m = 0 (1) và x² + mx + 2 = 0 (2) (với m là tham số). Tìm m để hai phương trình có ít nhất một nghiệm chung.

Lời giải

Chọn B

Bài 13: Cho phương trình x² + mx - 6m² = 0 với m là tham số. Chọn khẳng định sai:

Lời giải

Chọn A

Bài 14: Cho phương trình mx² - 2(m + 1)x + m + 2 = 0. Chọn kết luận đúng.

Lời giải

Chọn B

Bài 15: Khi phương trình x² + (m + 1)x - m = 0 có nghiệm kép, giá trị của nghiệm kép là:

Lời giải

Chọn C

Bài 16: Cho phương trình x² - 2x + 1 - m² = 0 với m là tham số. Khẳng định nào sau đây là đúng?

Lời giải

Chọn D

Bài 17: Giá trị nguyên nhỏ nhất của tham số m để phương trình x² - 2(m + 7)x + m² - 4 = 0 có hai nghiệm trái dấu là:

Lời giải

Chọn C

Bài 18: Phương trình 2x² + (2m - 1)x + m - 1 = 0 có hai nghiệm bằng nhau về giá trị tuyệt đối nhưng trái dấu nhau khi:

Lời giải

Chọn C

Bài 19: Tìm m để phương trình x² - 2(m - 2)x - 6m = 0 có nghiệm x₁; x₂ sao cho biểu thức x₁² + x₂² đạt giá trị nhỏ nhất.

Lời giải

Chọn D

Bài 20:Tìm m để mx² - 2(m + 1)x + m + 3 = 0 là phương trình bậc hai nhận x = -2 là nghiệm.

Lời giải

Chọn A

Bài 21: Tìm m để hai phương trình x² + x + m - 2 = 0 (1) và x² + (m - 2)x + 1 = 0 (2) có nghiệm chung.

Lời giải

Chọn D

2. Bài tập tự luận

Bài 1: Giải phương trình x2 - 3x = 0

Lời giải:

Ta có: x2 - 3x = 0 ⇔ x(x - 3) = 0

Vậy phương trình có hai nghiệm là x1 = 0; x2 = 3

Bài 2: Đưa các phương trình sau về dạng ax2 + bx + c = 0 rồi chỉ rõ các hệ số a, b, c của phương trình ấy. Các phương trình: 5x2 - 3x = 10x + 100; x2 = 900

Lời giải:

+ Ta có: 5x2 - 3x = 10x + 100 ⇔ 5x2 - 13x - 100 = 0

Hệ số a = 5; b = -13; c = -100

+ Ta có: x2 = 900 ⇔ x2 - 900 = 0

Hệ số a = 1, b = 0; c = -900

Bài 3: Giải các phương trình sau bằng cách thêm bớt thích hợp

a) x2 + 6x = -8

b) x2 + x = 7

Lời giải:

a) Ta có: x2 + 6x = -8 ⇔ x2 + 6x + 9 = -8 + 9

⇔ (x + 3)2 = 1 

Vậy phương trình đã cho có x = -2 hoặc x = -4

b) Ta có: 

Vậy phương trình đã cho có nghiệm là 

3. Bài tập tự luyện

Bài 1: Giải các phương trình bậc hai sau:

Bài 2: Tìm x, y trong các trường hợp sau: