20 Bài tập Ứng dụng của định lí Thalès trong tam giác lớp 8 (sách mới) có đáp án

Van Anh Ngày: 21-08-2024 Lớp 8

Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Ứng dụng của định lí Thalès trong tam giác được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Ứng dụng của định lí Thalès trong tam giác. Mời các bạn đón xem:

Bài tập Toán 8 Ứng dụng của định lí Thalès trong tam giác

A. Bài tập Ứng dụng của định lí Thalès trong tam giác

Bài 1: Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết $B B^{'} = 20$ m, $B C = 30$ m và $B^{'} C = 40$ m. Tính độ rộng $x$ của khúc sông.

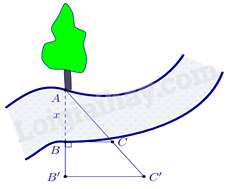
20 Bài tập Ứng dụng của định lí Thalès trong tam giác lớp 8 (sách mới) có đáp án (ảnh 7)

A.
30m
B.
60m
C.
90m
D.
120m

Hướng dẫn giải:

Đáp án : B

Dùng hệ quả của định lý Thalès, ta có:

$\frac{A B}{A B^{'}} = \frac{B C}{B^{'} C^{'}} \Rightarrow \frac{x}{x + 20} = \frac{30}{40} \Rightarrow x = 60$ m.

Bài 2: Bóng $(A K)$ của một cột điện $(M K)$ trên mặt đất dài 6m. Cùng lúc đó một cột đèn giao thông $(D E)$ cao 3m có bóng $(A E)$ dài 2m. Tính chiều cao của cột điện $(M K)$ .

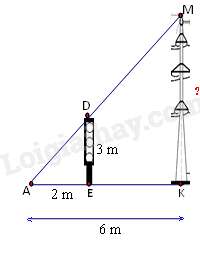
20 Bài tập Ứng dụng của định lí Thalès trong tam giác lớp 8 (sách mới) có đáp án (ảnh 6)

A.
6cm
B.
9cm
C.
12cm
D.
18cm

Hướng dẫn giải:

Đáp án : B

Ta có : DE // MK

$\Rightarrow \frac{D E}{M K} = \frac{A E}{A K}$

$\Leftrightarrow \frac{3}{M K} = \frac{2}{6}$

$\Rightarrow M K = \frac{6.3}{2} = 9$ (m)

Bài 3: Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm?

20 Bài tập Ứng dụng của định lí Thalès trong tam giác lớp 8 (sách mới) có đáp án (ảnh 4)

A.
80cm
B.
40cm
C.
160cm
D.
120cm

Hướng dẫn giải:

Đáp án : B

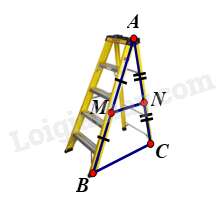
20 Bài tập Ứng dụng của định lí Thalès trong tam giác lớp 8 (sách mới) có đáp án (ảnh 3)

Gọi $M N$ là thanh ngang; $B C$ là độ rộng giữa hai bên thang.

$M N$ nằm chính giữa thang nên $M, N$ là trung điểm $A B$ và $A C$ .

$\Rightarrow \frac{A M}{A B} = \frac{A N}{A C} = \frac{1}{2}$

$\Rightarrow M N / / B C$ (định lí Thalès đảo)

$\Rightarrow \frac{A M}{A B} = \frac{A N}{A C} = \frac{M N}{B C}$ (hệ quả định lí Thalès)

$\Rightarrow M N = \frac{1}{2} B C = \frac{1}{2} \cdot 80 = 40$ (cm)

Vậy người thợ đã làm thanh ngang đó dài 40cm.

Bài 4: Nhà tâm lý học Abraham Maslow (1908 – 1970) được xem như một trong những người tiên phong trong trường phái Tâm lý học nhân văn. Năm 1943, ông đã phát triển Lý thuyết về Thang bậc nhu cầu của con người (như hình vẽ bên). Trong đó, $B K = 6$ cm. Hãy tính đoạn thẳng $C J; E H$ ?

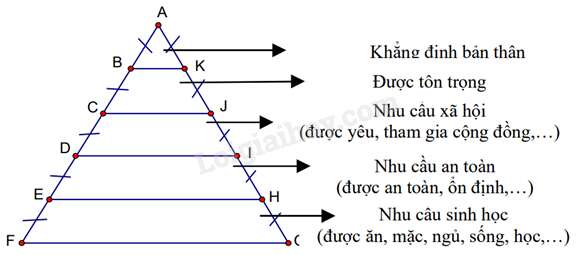
20 Bài tập Ứng dụng của định lí Thalès trong tam giác lớp 8 (sách mới) có đáp án (ảnh 2)

A.
$C J = 6 c m; E H = 12 c m$
B.
$C J = 12 c m; E H = 24 c m$
C.
$C J = 9 c m; E H = 18 c m$
D.
$C J = 12 c m; E H = 18 c m$

Hướng dẫn giải:

Đáp án : B

Ta có: $A B = B C = C D = D E = E F = \frac{A F}{5}$ ;

$A K = K J = J I = I H = H O = \frac{A O}{5}$

$\begin{array}{l} A C = A B + B C = 2 A B \Rightarrow \frac{A B}{A C} = \frac{1}{2} \\ A J = A K + K J = 2 A K \Rightarrow \frac{A K}{A J} = \frac{1}{2} \end{array}} \Rightarrow \frac{A B}{A C} = \frac{A K}{A J}$

$\Rightarrow B K / / C J$ (định lí Thalès đảo)

$\Rightarrow \frac{A B}{A C} = \frac{A K}{A J} = \frac{B K}{C J}$ (hệ quả định lí Thalès)

$\Rightarrow C J = 2 B K = 2.6 = 12$ cm

$\begin{array}{l} A E = A B + B C + C D + D E = 4 A B \Rightarrow \frac{A C}{A E} = \frac{2 A B}{4 A B} = \frac{1}{2} \\ A H = A K + K J + J I + I H = 4 A K \Rightarrow \frac{A J}{A H} = \frac{2 A K}{4 A K} = \frac{1}{2} \end{array}} \Rightarrow \frac{A C}{A E} = \frac{A J}{A H}$

$\Rightarrow C J / / E H$ (định lí Thalès đảo)

$\Rightarrow \frac{A C}{A E} = \frac{A J}{A H} = \frac{C J}{E H}$ (hệ quả định lí Thalès)

$\Rightarrow E H = 2 C J = 2.12 = 24$ cm

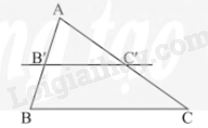
Bài 5: Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái $P Q = 1, 5$ m. Chú thợ nhẩm tính chiều dài mái $D E$ biết $Q$ là trung điểm $E C$ , $P$ là trung điểm của $D C$ . Em hãy tính giúp chú thợ xem chiều dài mái $D E$ bằng bao nhiêu (xem hình vẽ minh họa)?

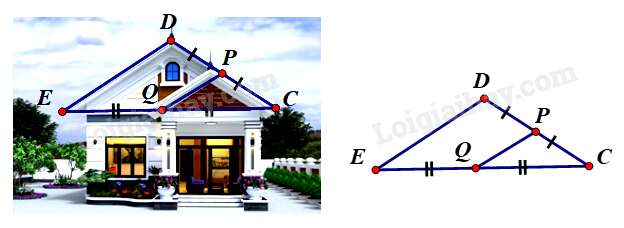
20 Bài tập Ứng dụng của định lí Thalès trong tam giác lớp 8 (sách mới) có đáp án (ảnh 1)

A.
3m
B.
6m
C.
9m
D.
12m

Hướng dẫn giải:

Đáp án : A

Vì $Q$ là trung điểm $E C$ , $P$ là trung điểm của $D C$ nên

$\frac{C Q}{C E} = \frac{C P}{C D} = \frac{1}{2}$

$\Rightarrow Q P / / E D$ (định lí Thalès đảo)

$\Rightarrow \frac{C Q}{C E} = \frac{C P}{C D} = \frac{Q P}{E D}$ (hệ quả định lí Thalès)

$\Rightarrow D E = 2 P Q = 2.1, 5 = 3$ (m)

Vậy chiều dài mái $D E$ bằng 3m.

B. Lý thuyết Ứng dụng của định lí Thalès trong tam giác

1. Tỉ số của hai đoạn thẳng

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là:

Chú ý:

- Để tính tỉ số của hai đoạn thẳng, ta phải đưa chúng về cùng một đơn vị đo.

- Tỉ số của hai đoạn thẳng đó không phụ thuộc vào đơn vị đo độ dài đoạn thẳng.

Đoạn thẳng tỉ lệ

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: hay

2. Định lí Thalès

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.

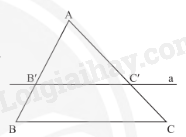
Lý thuyết Định lí Thalès trong tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

3. Hệ quả của định lí Thalès

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

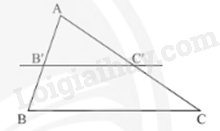
Lý thuyết Định lí Thalès trong tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 2)

4. Định lí Thalès đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

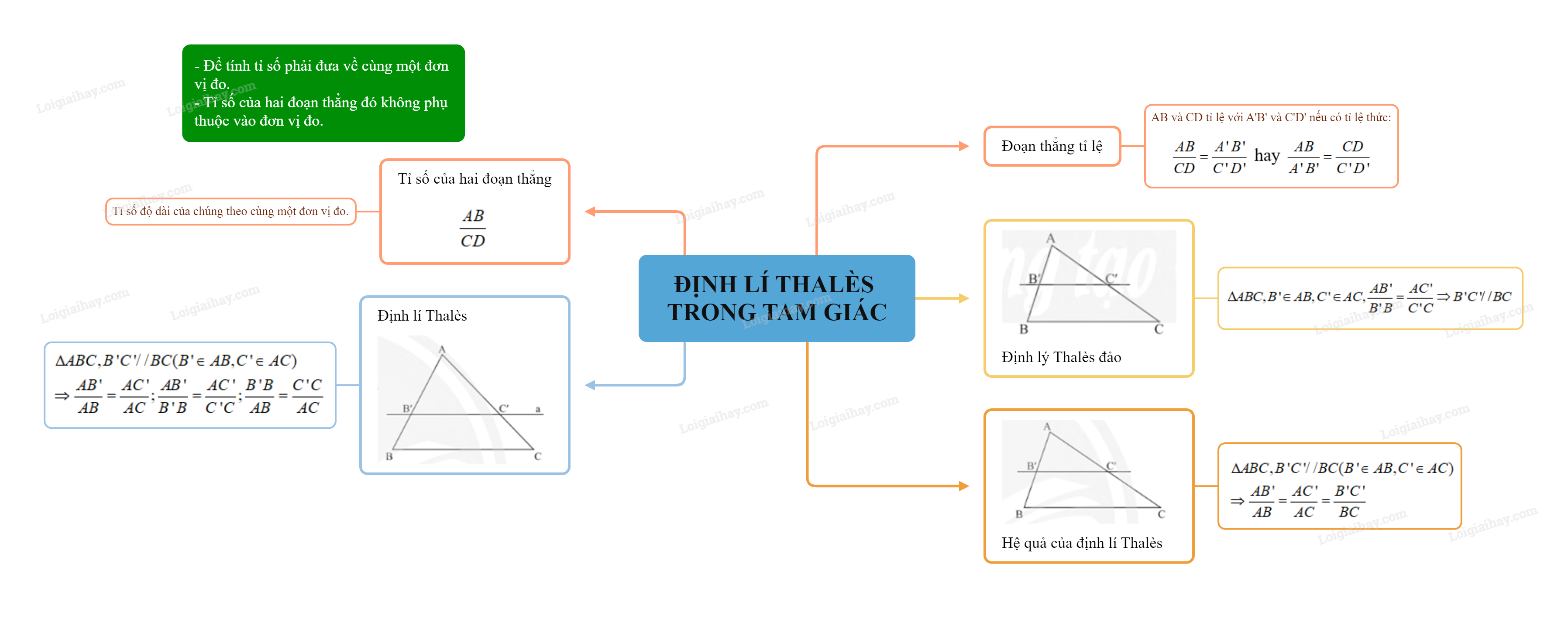
Lý thuyết Định lí Thalès trong tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 3)