Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 9 Bất đẳng thức và tính chất được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bất đẳng thức và tính chất. Mời các bạn đón xem:

Bài tập Toán 9 Bất đẳng thức và tính chất

A. Bài tập Bất đẳng thức và tính chất

Bài 1. Cho a > b. Khi đó ta có:

A. 2a > 7b.

B. 2a > 2b + 1.

C. 5a + 2 > 5b + 2.

D. –6a < –6b – 1.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: a > b, suy ra 5a > 5b, do đó 5a + 2 > 5b + 2.

Bài 2. Xác định vế trái và vế phải của bất đẳng thức sau:

a) –3x + 2 > 7;

b) 2x – 1 ≤ 3x + 5;

c) x² + 2 ≥ 0.

Hướng dẫn giải

a) Vế trái là –3x + 2, vế phải là 7;

b) Vế trái là 2x – 1, vế phải là 3x + 5;

c) Vế trái là x² + 2, vế phải là 0.

Bài 3. Bất đẳng thức m ≥ 7 có thể được phát biểu là

A. m lớn hơn 7.

B. m nhỏ hơn 7.

C. m không nhỏ hơn 7.

D. m không lớn hơn 7.

Hướng dẫn giải

Đáp án đúng là: C

Bất đẳng thứcm ≥ 7 có thể được phát biểu là m lớn hơn hoặc bằng 7 hay m không nhỏ hơn 7.

Bài 4. Hệ thức nào sau đây là bất đẳng thức?

A. x + 6 = 0.

B. y² + 1 ≥ 0.

C. x² – 7x + 6 = 0.

D. 3x = y.

Hướng dẫn giải

Đáp án đúng là: B

• Các hệ thức x + 6 = 0; x² – 7x + 6 = 0; 3x = y là đẳng thức.

• Hệ thức y² ≥ 0 là bất đẳng thức.

Bài 5. Cho a > b, hãy so sánh:

a) a – 2 và  b – 2.

b) –5a và –5b.

c) 10 – 3a và 10 – 3b.

d) 12a + 1 và 12b – 4.

e) 2 – 9a và 5 – 9b.

Hướng dẫn giải

a) Do a > b nên a – 2 > b – 2.

b) Do a > b nên –5a < –5b.

c) Do a > b nên –3a < –3b, suy ra 10 – 3a < 10 – 3b.

d) Do a > b nên 12a > 12b, suy ra 12a + 1 > 12b + 1.

Mà 12b + 1 > 12b + 1 – 5 hay 12b + 1 > 12b – 4.

Vậy 12a + 1 > 12b – 4.

e) Do a > b nên –9a < –9b, suy ra 2 – 9a < 2 – 9b.

Mà 2 – 9b < 2 – 9b + 3 hay 2 – 9b < 5 – 9b.

Vậy 2 – 9a < 5 – 9b.

B. Lý thuyết Bất đẳng thức và tính chất

1. Bất đẳng thức

Nhắc lại thứ tự trên tập số thực

Trên tập số thực, với hai số a và b có ba trường hợp sau:

a) Số a bằng số b, kí hiệu $a=b$.

b) Số a lớn hơn số b, kí hiệu $a>b$.

c) Số a nhỏ hơn số b, kí hiệu $a<b$.

Khi biểu kiễn số thực trên trục số, điểm biểu diễn số bé hơn nằm trước điểm biểu diễn số lớn hơn.

Số a lớn hơn hoặc bằng số b, tức là $a>b$ hoặc $a=b$, kí hiệu là $a\ge b$.

Số a nhỏ hơn hoặc bằng số b, tức là $a<b$ hoặc $a=b$, kí hiệu là $a\le b$.

Khái niệm bất đẳng thức

Chú ý:

Hai bất đẳng thức $1<2$ và $-3<-2$ (hay $6>3$ và $8>5$) được gọi là hai bất đẳng thức cùng chiều.

Hai bất đẳng thức $1<2$ và $-2>-3$ (hay $6>3$ và $5<8$) được gọi là hai bất đẳng thức ngược chiều.

Tính chất bắc cầu của bất đẳng thức

Ví dụ: Vì $\frac{2024}{2023}=1+\frac{1}{2023}>1$ và $\frac{2021}{2022}=1-\frac{1}{2022}<1$ nên $\frac{2024}{2023}>\frac{2021}{2022}$.

2. Liên hệ giữa thứ tự và phép cộng

Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

Ví dụ: Vì $2023<2024$ nên $2023+\left(-19\right)<2024+\left(-19\right)$

3. Liên hệ giữa thứ tự và phép nhân

- Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.

Ví dụ:

Vì $-7<-5$ và $3>0$ nên $3.\left(-7\right)<3.\left(-5\right)$.

Vì $-7<-5$ và $-3<0$ nên $\left(-3\right).\left(-7\right)>\left(-3\right).\left(-5\right)$.

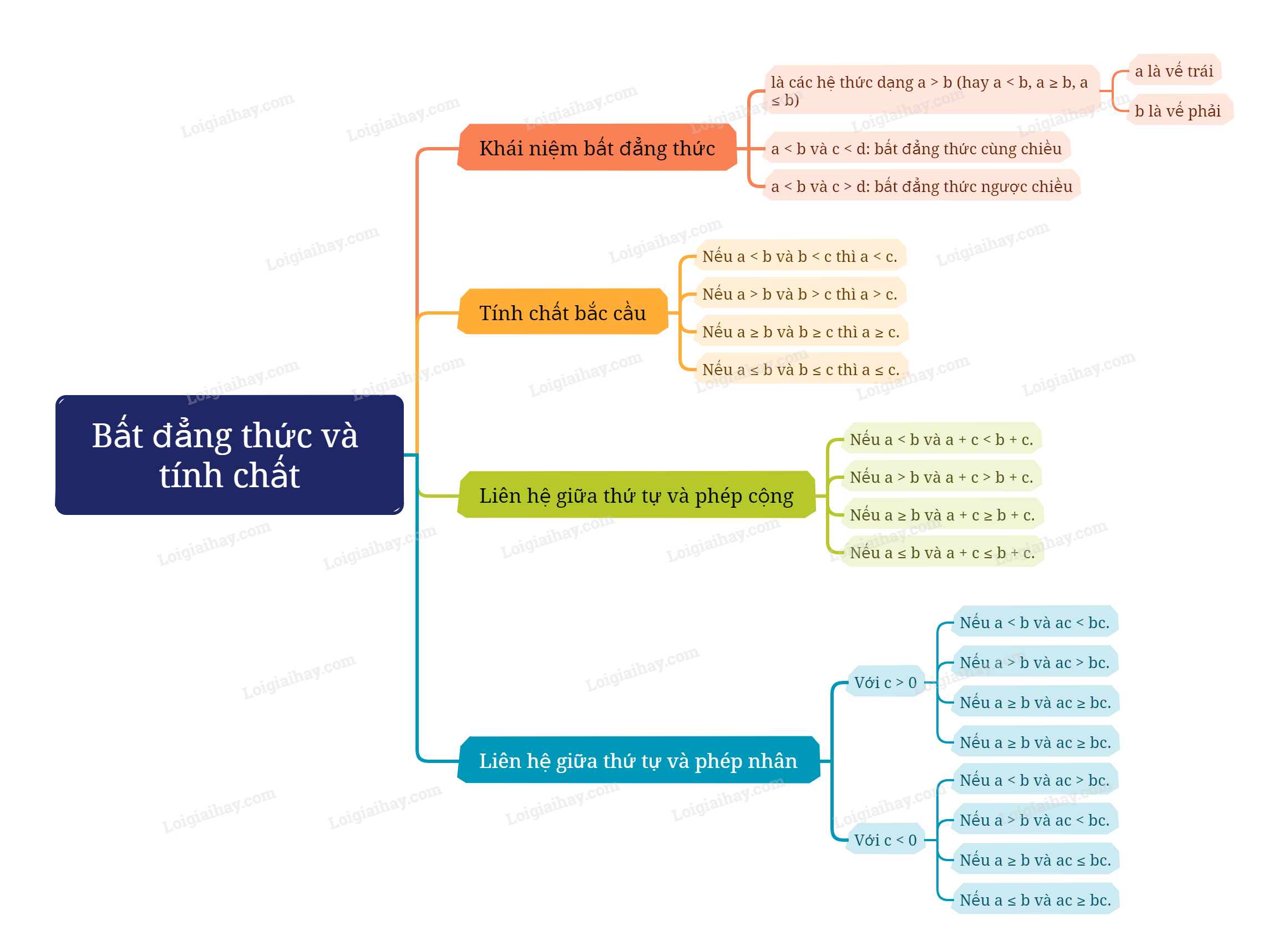
Sơ đồ tư duy Bất đẳng thức và tính chất