Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 9 Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn . Mời các bạn đón xem:

Bài tập Toán 9 Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

A. Bài tập Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

Bài 1. Cặp số nào sau đây là nghiệm của phương trình 5x + 4y = 8?

A. (–2; 1).

B. (0; 2).

C. (–1; 0).

D. (4; 3).

Hướng dẫn giải

Đáp án đúng là: B

Xét phương trình 5x + 4y = 8:

⦁ Thay x = –2 và y = 1, ta có: 5.(–2) + 4.1 = –2 ≠ 8.

⦁ Thay x = 0 và y = 2, ta có: 5.0 + 4.2 = 8.

⦁ Thay x = –1 và y = 0, ta có: 5.(–1) + 4.0 = –5 ≠ 8.

⦁ Thay x = 4 và y = 3, ta có: 5.4 + 4.3 = 32 ≠ 8.

Vậy (0; 2) là nghiệm của phương trình đã cho.

Bài 2. Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) 2x – y = 3;

b) x + 0y = −2.

Hướng dẫn giải

a) Viết lại phương trình thành y = 2x – 3.

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = 2x – 3 (như hình vẽ).

b) Viết lại phương trình thành x = −2.

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với Ox tại điểm M(−2; 0).

Bài 3. Để chuẩn bị cho buổi liên hoan của gia đình, cô Lan mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là 120 nghìn đồng/kg, giá tiền cá chép là 50 nghìn đồng/kg. Cô Lan đã chi 290 nghìn để mua 3 kg hai loại thực phẩm trên. Gọi x và y lần lượt là số kilôgam thịt lợn và cá chép mà cô Lan đã mua.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (2; 1) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Hướng dẫn giải

a) Cô Lanđã mua 3 kg hai loại thực phẩm (thịt lợn và cá chép) nên ta có phương trình: x + y = 3. (1)

Số tiền cô Lan đã chi để mua x kilôgam thịt lợn là 120x (nghìn đồng).

Số tiền cô Lan đã chi để mua y kilôgam cá chép là 50y (nghìn đồng).

Theo bài, cô Lan đã chi 295 nghìn để mua hai loại thực phẩm trên nên ta có phương trình: 120x + 50y = 290. (2)

Từ (1) và (2) ta có hệ phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng: $\left\{\begin{array}{l}x+y=3\\ 120x+50y=290.\end{array}\right.$

b) Thay x = 2 và y = 1 vào mỗi phương trình trong hệ$\left\{\begin{array}{l}x+y=3\\ 120x+50y=290\end{array}\right.$ta có:

2 + 1 = 3;

120. 2 + 50. 1 = 240 + 50 = 290.

Do đó, cặp số (2; 1) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (2; 1) là nghiệm của hệ phương trình ở câu a.

Bài 4. Xét trò ném đồng xu vào trong vòng tròn như hình vẽ dưới đây:

– Lượt chơi thứ nhất (ném đồng xu 2 lần): một đồng xu rơi vào phần trong (hình tròn màu trắng), một đồng xu rơi vào phần ngoài (hình vành khăn màu đen); tổng số điểm đạt được là 17 (điểm).

– Lượt chơi thứ hai (ném đồng xu 5 lần): hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài; tổng số điểm đạt được là 41 (điểm).

Gọi x, y lần lượt là số điểm ấn định cho phần trong và phần ngoài.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (10; 7) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Hướng dẫn giải

a) – Lượt chơi thứ nhất có một đồng xu rơi vào phần trong và một đồng xu rơi vào phần ngoài, đạt được 17 điểm nên ta có phương trình: x + y = 17.

– Lượt chơi thứ hai có hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài, đạt được 41 điểm nên ta có phương trình: 2x + 3y = 41.

Vậy hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng là: $\left\{\begin{array}{l}x+y=17\\ 2x+3y=41.\end{array}\right.$

b) Thay x = 10 và y = 7 vào mỗi phương trình trong hệ ở câu a, ta có:

10 + 7 = 17;

2.10 + 3.7 = 41.

Suy ra cặp số (10; 7) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (10; 7) là nghiệm của hệ phương trình ở câu a.

Bài 5. Cặp số nào sau đây là nghiệm của hệ phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}4x-5y=3\\ 3x-y=16\end{array}\right.?$

A. (–1; 3).

B. (2; 1).

C. (7; 5).

D. (5; –1).

Hướng dẫn giải

Đáp án đúng là: C

 ⦁ Thay x = –1 và y = 3 vào mỗi phương trình trong hệ, ta có:

4.(–1) – 5.3 = –19 ≠ 3;

3.(–1) – 3 = –6 ≠ 16.

Do đó cặp số (–1; 3) không là nghiệm của mỗi phương trình trong hệ.

Vậy cặp số (–1; 3) không là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 2 và y = 1 vào mỗi phương trình trong hệ, ta có:

4.2 – 5.1 = 3;

3.2 – 1 = 5 ≠ 16.

Do đó cặp số (2; 1) không là nghiệm của phương trình thứ hai trong hệ.

Vậy cặp số (2; 1) không là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 7 và y = 5 vào mỗi phương trình trong hệ, ta có:

4.7 – 5.5 = 3;

3.7 – 5 = 16.

Suy ra cặp số (7; 5) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (7; 5) là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 5 và y = –1 vào mỗi phương trình trong hệ, ta có:

4.5 – 5.(–1) = 25 ≠ 3;

3.5 – (–1) = 16.

Do đó cặp số (5; –1) không là nghiệm của phương trình thứ nhất trong hệ.

Vậy cặp số (5; –1) không là nghiệm của hệ phương trình đã cho.

Ta chọn phương án C.

B. Lý thuyết Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

1. Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn

Ví dụ: $2x+3y=4$, $0x+2y=3$, $x+0y=2$ là các phương trình bậc nhất hai ẩn.

Nghiệm của phương trình bậc nhất hai ẩn

Ví dụ: Cặp số $(-1;2)$ là nghiệm của phương trình $2x+3y=4$ vì $2.\left(-1\right)+3.2=-2+6=4$.

Cặp số $(1;2)$ không là nghiệm của phương trình $2x+3y=4$ vì

$2.1+3.2=2+6=8\ne 4$.

Biểu diễn nghiệm trên mặt phẳng tọa độ Oxy

- Mỗi nghiệm $\left(x_0;y_0\right)$ của phương trình $ax+by=c$ được biểu diễn bởi điểm có tọa độ $\left(x_0;y_0\right)$ trên mặt phẳng tọa độ.

- Phương trình bậc nhất hai ẩn $ax+by=c$ luôn luôn có vô số nghiệm. Tất cả các nghiệm của phương trình đó được biểu diễn bởi một đường thẳng.

Ví dụ:

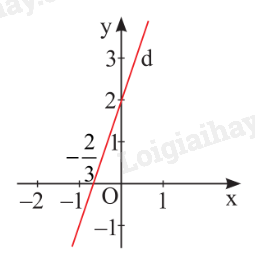
Nghiệm của phương trình $-3x+y=2$ được biểu diễn bởi đường thẳng d: $y=3x+2$.

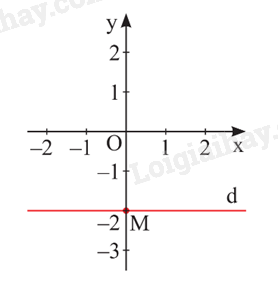
Nghiệm của phương trình $0x+y=-2$ được biểu diễn bởi đường thẳng d: $y=-2$ vuông góc với Oy tại điểm $M\left(0;-2\right)$.

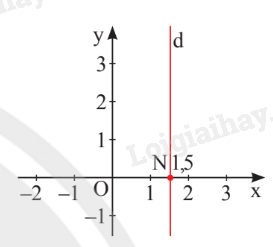
Nghiệm của phương trình $2x+0y=3$ được biểu diễn bởi đường thẳng d: $x=1,5$ vuông góc với Ox tại điểm $N\left(1,5;0\right)$.

2. Hệ hai phương trình bậc nhất hai ẩn

Khái niệm hệ hai phương trình bậc nhất hai ẩn

Ví dụ: Hệ phương trình $\{\begin{array}{l}2x-y=0\\ x+y=3\end{array}$, $\{\begin{array}{l}3x=1\\ x-y=3\end{array}$, $\{\begin{array}{l}4x-y=3\\ 3y=6\end{array}$ là các hệ phương trình bậc nhất hai ẩn.

Nghiệm của hệ hai phương trình bậc nhất hai ẩn

Ví dụ: Cặp số (1; 2) là một nghiệm của hệ phương trình $\{\begin{array}{l}2x-y=0\\ x+y=3\end{array}$, vì:

$2x-y=2.1-2=0$ nên (1; 2) là nghiệm của phương trình thứ nhất.

$x+y=1+2=3$ nên (1; 2) là nghiệm của phương trình thứ hai.

Sơ đồ tư duy Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn