Tài liệu chuyên đề Số hữu tỉ Toán lớp 7 gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán lớp 7. 

Chỉ từ 500k mua trọn bộ Chuyên đề dạy thêm Toán lớp 7 word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Số hữu tỉ

Phần I. TÓM TẮT LÝ THUYẾT

1. Số hữu tỉ:

Định nghĩa:

a.  Số hữu tỉ được viết dưới dạng $\frac{a}{b}$$(a,b\in \mathrm{\mathbb{Z}}, b\ne 0)$

b. VD: Các số: $\frac{1}{2}; -\frac{4}{3}; \frac{3}{1}; 2\frac{5}{7}$ là các số hữu tỉ .

c. Kí hiệu tập hợp số hữu tỉ là $\mathrm{\mathbb{Q}}$.

2. Cộng trừ các số hữu tỉ

Cho hai số hữu tỉ : $x = \frac{a}{m}; y =\frac{b}{m}$(trong đó: a; b; m $\in \mathrm{\mathbb{Z}}$, m ≠ 0) 

Khi đó ta có cộng thức:

3. Nhân chia các số hữu tỉ.

Cho hai số hữu tỉ : $x= \frac{a}{b}; y= \frac{c}{d}$ (trong đó:a; b; m $\in \mathrm{\mathbb{Z}}$, m ≠ 0).

Khi đó ta có cộng thức:

4. Giá trị tuyệt đối của một số hữu tỉ

5. Lũy thừa của một số hữu tỉ

Nhắc lại về lũy thừa: 

Trong đó: x được gọi là cơ số, n được gọi là số mũ

Khi x là số hữu tỉ: 

Do đó ta có cộng thức tổng quát: ${\left(\frac{a}{b}\right)}^n=\frac{a^n}{b^n}$

Các cộng thức liên quan đến lũy thừa cùng cơ số

Các cộng thức về cùng lũy thừa khác cơ số:  ${\left(a.b\right)}^n=a^n.b^n +{\left(\frac{a}{b}\right)}^n= \frac{a^n}{b^n}$

6. Tỉ lệ thức

Định nghĩa: Tỉ lệ thức là đẳng thức của hai tỉ số có dạng $\frac{a}{b}=\frac{c}{d}$

Tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ còn được viết là: a : b = c : d

- Các ngoại tỉ: a và d                                       - Các trung tỉ: b và c

7. Số thập phân hữu hạn và số thập phân vô hạn tuần tuần hoàn

 Mỗi số hữu tỉ được biểu diễn bởi số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ngược lại, mỗi số thập phân hữu hạn hoặc vô hạn tuần hoàn điều biểu diện được dưới dạng số hữu tỉ.

8. Làm tròn số

Quy ước làm tròn số:

Trường hợp 1:

Nếu chữ số đầu tiên trong các chữ số bị bỏ đi nhỏ hơn 5 thì ta giữ nguyên bộ phận còn lại. Trong trường hợp số nguyên thì ta thay các chữ số bị bỏ đi bằng chữ số 0.

Trường hợp 2:

Nếu chữ số đầu tiên trong các chữ số bị bỏ đi lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào  chữ số cuối cùng của bộ phận còn lại. Trong trường hợp số nguyên thì ta thay các chữ số bị bỏ đi bằng chữ số 0.

9. Số vô tỉ và số thực

a. Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Tập hợp các số vô tỉ là I.

b. Căn bậc hai của một số a không âm là số x sao cho $x^2 =a$

c. Số thực: Số hữu tỉ và số vô tỉ được gọi chung là số thực.

Tập hợp các số thực được kí hiệu là: $\mathrm{ℝ}$

Phần II. CÁC DẠNG TOÁN THƯỜNG GẶP

Chủ đề 1: SỐ HỮU TỈ VÀ CÁC PHÉP TOÁN LIÊN QUAN

Dạng 1: NHẬN BIẾT MỘT SỐ HỮU TỈ

A. PHƯƠNG PHÁP

Để nhận biết một số có phải là số hữu tỉ chuyển số đó về phân số tối giản (Tức phân số không thể rút gọn được nữa). Nếu chuyển được về dạng $\frac{a}{b}$(trong đó a,b là những số nguyên và b là số khác 0). Thì kết luận số đó là số hữu tỉ, ngược lại số đó không phải là số hữu tỉ.

* Lưu ý: Một số nguyên bất kỳ cũn được xem là số hữu tỉ.

B. BÀI TẬP MẪU CÓ HƯỚNG DẪN GIẢI

Bài tập mẫu 1: Xét xem các số sau đây có phải là số hữu tỉ hay không? Tại sao?

a. $\frac{4}{3}$

b. $\frac{-1}{2}$

c. 0,8

d.$3\frac{1}{3}$

Hướng dẫn giải

a. Ta có  $\frac{4}{3}$ là số hữu tỉ.

Thật vậy: 4 và 3 đều là những số nguyên và 3 khác 0

b. Ta có $\frac{-1}{2}$  là số hữu tỉ

Thật vậy: -1 và 2 là những số nguyên và 2 khác 0

c. Ta có 0,8 là số hữu tỉ

Ta có biến đổi: $0,8 = \frac{8}{10 }=\frac{4}{5}$, ta có: 4 và 5 là những số nguyên và 5 khác 0

d. Ta có: $3\frac{1}{3}$ là số hữu tỉ

Ta có: $3\frac{1}{3}=\frac{10}{3}$ , ta có: 10 và 3 là những số nguyên và 3 khác 0.      

Bài tập mẫu 2: Dùng ký hiệu 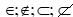 điền vào chổ trống sau:

Hướng dẫn giải

C. BÀI  TẬP LUYỆN TẬP CÓ ĐÁP ÁN

 Bài tập 1: Xét xem các số sau đây có phải là số hữu tỉ hay không? Tại sao?

a. $-\frac{1}{9}$

b. $5.7^2$

c. -0,125

d. $-9\frac{1}{3}$

Bài tập 2: Dùng ký hiệu 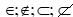 điền vào chổ trống sau:

Bài tập 3. Điền k‎ý hiêụ 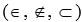 thích hợp vào ô vuông:

Bài tập 4:  Điền các kí hiệu $\mathrm{\mathbb{N}}, \mathrm{\mathbb{Z}}, \mathrm{\mathbb{Q}}$ vào ô trống cho hợp nghĩa (điền tất cả các khả năng có thể):

D. HƯỚNG DẪN GIẢI HOẶC ĐÁP SỐ

Bài tập 1: Các số đều là số hữu tỉ. Bạn đọc giải thích như Bài tập mẫu 1.

Bài tập 2: Dùng ký hiệu 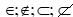 điền vào chổ trông sau:

Bài tập 3. Điền ký hiêụ 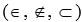 thích hợp vào ô vuông:

Bài tập 4: Điền các kí hiệu $\mathrm{\mathbb{N}}, \mathrm{\mathbb{Z}}, \mathrm{\mathbb{Q}}$ vào ô trống cho hợp nghĩa (điền tất cả các khả năng có thề):

Dạng 2: BIỂU DIỄN MỘT SỐ HỮU TỈ LÊN TRỤC SỐ

A. PHƯƠNG PHÁP

+ Bước 1: Biến đổi số cần biểu diễn thành phân số tối giản hoặc hổn số nếu phân số đó lớn hơn 1.

+ Bước 2: Biểu diễn số 0 nằm chỉnh giữa trục số. Quy ước chiều bên phải là chiều dương, chiều bên trái là chiều âm. Tùy vào số cần biểu diễn để biểu diễn lên đúng chiều.

+ Bước 3: Nếu là hỗ số, đếm phần nguyên đúng vị trí của phần chia. Tiếp tục chia đơn vị tiếp theo thành b đoạn nhỏ (b là mẫu của số hữu tỉ). Tiếp tục đếm a đoạn trên phần đã chia. Điểm biểu diễn phân số $\frac{a}{b}$ chỉnh là vị trí của số hữu tỉ cần biểu diễn lên trục số.

................................

................................

................................