Với giải Bài 2 trang 88 Toán 11 Tập 2 Cánh diều chi tiết trong Bài 2: Đường thẳng vuông góc với mặt phẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 2 trang 88 Toán 11 Tập 2: Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).
a) Xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC).
b) Giả sử BC ⊥ SA, CA ⊥ SB. Chứng minh rằng H là trực tâm của tam giác ABC và AB ⊥ SC.
Lời giải:
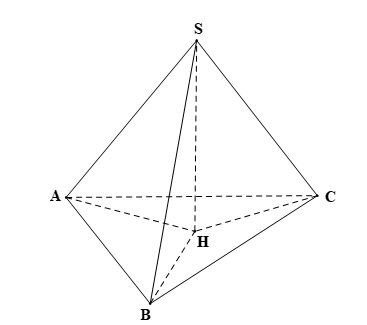
a) Ta có: H là hình chiếu của S trên mặt phẳng (ABC); A ∈ (ABC).
Suy ra HA là hình chiếu của SA trên mặt phẳng (ABC).
Tương tự ta có HB, HC lần lượt là hình chiếu của SB và SC trên mặt phẳng (ABC).
b) Do H là hình chiếu của S trên mặt phẳng (ABC) nên SH ⊥ (ABC).
Mà AB, AC, BC đều nằm trên (ABC).
Từ đó ta có: SH ⊥ AB, SH ⊥ AC, SH ⊥ BC.
· Ta có: BC ⊥ SH, BC ⊥ SA và SH ∩ SA = S trong (SAH).
Suy ra BC ⊥ (SAH).
Mà AH ⊂ (SAH) nên BC ⊥ AH. (1)
· Ta có: AC ⊥ SB, AC ⊥ SH và SB ∩ SH = S trong (SBH).
Suy ra AC ⊥ (SBH).
Mà BH ⊂ (SBH) nên AC ⊥ BH. (2)
Từ (1) và (2) ta có H là trực tâm của tam giác ABC.
Suy ra AB ⊥ CH.
· Ta có: AB ⊥ CH, AB ⊥ SH và CH ∩ SH = H trong (SCH).
Suy ra AB ⊥ (SCH).
Mà SC ⊂ (SCH) nên AB ⊥ SC.
Xem thêm các lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Câu hỏi khởi động trang 80 Toán 11 Tập 2: Trong Hình 9, cột gỗ thẳng đứng và sàn nhà nằm ngang gợi nên hình ảnh đường thẳng vuông góc với mặt phẳng...
Hoạt động 1 trang 80 Toán 11 Tập 2: Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền nhà. Coi dây dọi như đường thẳng d và nền nhà như mặt phẳng (P), khi đó Hình 10 gợi nên hình ảnh đường thẳng d vuông góc với mặt phẳng (P). Người thợ xây đặt chiếc thước thẳng ở một vị trí tùy ý trên nền nhà. Coi chiếc thước thẳng đó là đường thẳng a trong mặt phẳng (P), nêu dự đoán về mối liên hệ giữa đường thẳng d và đường thẳng a...
Hoạt động 2 trang 81 Toán 11 Tập 2: Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d, a, b; sàn nhà coi như mặt phẳng (P) chứa a và b. Hỏi đường thẳng d có vuông góc với mặt phẳng (P) hay không?...
Luyện tập 1 trang 81 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA ⊥ (ABCD). Chứng minh rằng BD ⊥ (SAC)...
Hoạt động 3 trang 81 Toán 11 Tập 2: Cho điểm O và đường thẳng a. Gọi b, c là hai đường thẳng phân biệt cùng đi qua điểm O và cùng vuông góc với đường thẳng a (Hình 14)...
Luyện tập 2 trang 81 Toán 11 Tập 2: Hình 17 mô tả một cửa gỗ có dạng hình chữ nhật, ở đó nẹp cửa và mép dưới cửa lần lượt gợi nên hình ảnh hai đường thẳng d và a. Điểm M là vị trí giao giữa mép gắn bản lề và mép dưới của cửa. Hãy giải thích tại sao khi quay cánh cửa, mép dưới cửa là những đường thẳng a luôn nằm trên mặt phẳng đi qua điểm M cố định và vuông góc với đường thẳng d...
Hoạt động 4 trang 82 Toán 11 Tập 2: Cho mặt phẳng (P) và điểm O. Gọi a, b là hai đường thẳng cắt nhau thuộc mặt phẳng (P) sao cho a và b không đi qua O. Lấy hai mặt phẳng (Q), (R) lần lượt đi qua O và vuông góc a, b (Hình 18)...
Luyện tập 3 trang 82 Toán 11 Tập 2: Cho mặt phẳng (P) và đường thẳng a cắt nhau tại điểm O, a ⊥ (P). Giả sử điểm M thỏa mãn OM ⊥ (P). Chứng minh rằng M ∈ a...
Hoạt động 5 trang 83 Toán 11 Tập 2: Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P)...
Luyện tập 4 trang 84 Toán 11 Tập 2: Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d và khác O; các điểm A’, B’ thuộc (P) thỏa mãn AA’ ⊥ (P), BB’ ⊥ (P). Chứng minh rằng...
Hoạt động 6 trang 84 Toán 11 Tập 2: Trong Hình 21, hai mặt trần của nhà cao tầng và cột trụ bê tông gợi nên hình ảnh hai mặt phẳng (P), (Q) phân biệt và đường thẳng a...
Luyện tập 5 trang 85 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Mặt phẳng (P) khác với mặt phẳng (ABC), vuông góc với đường thẳng SA và lần lượt cắt các đường thẳng SB, SC tại hai điểm phân biệt B’, C’. Chứng minh rằng B’C’ // BC...
Hoạt động 7 trang 85 Toán 11 Tập 2: Cho mặt phẳng (P). Xét một điểm M tuỳ ý trong không gian...
Luyện tập 6 trang 86 Toán 11 Tập 2: Cho mặt phẳng (P) và đoạn thẳng AB. Xác định hình chiếu của đoạn thẳng AB trên mặt phẳng (P)...
Hoạt động 8 trang 87 Toán 11 Tập 2: Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P), đường thẳng a’ là hình chiếu của đường thẳng a trên mặt phẳng (P), đường thẳng d nằm trong mặt phẳng (P). Quan sát Hình 27 và cho biết:..
Luyện tập 7 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông...
Bài 1 trang 88 Toán 11 Tập 2: Quan sát Hình 30 (hai cột của biển báo, mặt đường), cho biết hình đó gợi nên tính chất nào về quan hệ vuông góc giữa đường thẳng và mặt phẳng...
Bài 2 trang 88 Toán 11 Tập 2: Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC)...
Bài 3 trang 88 Toán 11 Tập 2: Cho tứ diện ABCD có AB ⊥ (BCD), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:...
Bài 4 trang 88 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng:...
Bài 5 trang 88 Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABC), BC ⊥ AB. Lấy hai điểm M, N lần lượt là trung điểm của SB, SC và điểm P nằm trên cạnh SA. Chứng minh rằng tam giác MNP là tam giác vuông...
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Hai đường thẳng vuông góc
Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 4: Hai mặt phẳng vuông góc
Bài 5: Khoảng cách