Với giải Khám phá 1 trang 67 Toán 8 Tập 2 Chân trời sáng tạo chi tiết trong Bài 2: Các trường hợp đồng dạng của hai tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 2: Các trường hợp đồng dạng của hai tam giác
Khám phá 1 trang 67 Toán 8 Tập 2: Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N sao cho AM = 2 cm, AN = 3 cm.
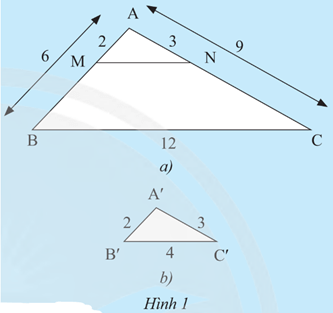
a) So sánh các tỉ số .
b) Tính độ dài đoạn thẳng MN.
c) Em có nhận xét gì về mối quan hệ giữa các tam giác ABC, AMN và A'B'C'.
Lời giải:
a) Ta có: ;
;
.
Do đó .
b) Tam giác ABC có , theo định lí Thalès đảo suy ra MN // BC.
Khi đó ΔAMN ᔕ ΔABC nên suy ra MN = 4.
c) Xét tam giác AMN và A'B'C' có:
• MN = B'C' = 4;
• AM = A'B' = 2;
• AN = A'C' = 3.
Suy ra ΔAMN = ΔA′B′C′ (c.c.c).
Nhận xét: ΔAMN = ΔA′B′C′, ΔA′B′C′ ᔕ ΔABC và ΔAMN ᔕ ΔABC.
Xem thêm các lời giải bài tập Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Khởi động trang 67 Toán 8 Tập 2: Các trường hợp đồng dạng của hai tam giác có điều gì khác với các trường hợp bằng nhau của hai tam giác?...
Khám phá 1 trang 67 Toán 8 Tập 2: Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N sao cho AM = 2 cm, AN = 3 cm...
Thực hành 1 trang 68 Toán 8 Tập 2: Tìm trong Hình 4 các cặp tam giác đồng dạng...
Khám phá 2 trang 68 Toán 8 Tập 2: Cho tam giác DEF và ABC có (Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE. Qua M kẻ MN // BC (N ∈ AC)...
Thực hành 2 trang 69 Toán 8 Tập 2: Cho tam giác ADE và tam giác ACF có các kích thước như trong Hình 8. Chứng minh rằng ΔADE ᔕ ΔACF...
Khám phá 3 trang 69 Toán 8 Tập 2: Cho hai tam giác ABC và A'B'C' có (Hình 9)...
Thực hành 3 trang 70 Toán 8 Tập 2: Quan sát Hình 12...
Vận dụng 1 trang 70 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có AB = 6 m, CD = 15 m, OD = 8 m (Hình 13). Tính độ dài đoạn thẳng OB...
Vận dụng 2 trang 70 Toán 8 Tập 2: Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở Hoạt động khởi động (trang 67)...
Bài 1 trang 70 Toán 8 Tập 2: a) Tam giác AFE và MNG ở Hình 14 có đồng dạng với nhau không? Vì sao?...
Bài 2 trang 70 Toán 8 Tập 2: Tam giác ABC có độ dài AB = 4 cm, AC = 6 cm, BC = 9 cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác A'B'C'...
Bài 3 trang 70 Toán 8 Tập 2: Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 660 m. Nam chạy bốn vòng trên con đường bên trong, Hùng chạy hai vòng trên con đường bên ngoài. So sánh quãng đường chạy được của hai bạn...
Bài 4 trang 71 Toán 8 Tập 2: Xét xem cặp tam giác nào trong các Hình 16a, 16b đồng dạng?...
Bài 5 trang 71 Toán 8 Tập 2: Trong Hình 17, cho biết DE = 6 cm, EF= 7,8 cm, NP = 13 cm, NM = 10 cm, và . Tính ...
Bài 6 trang 71 Toán 8 Tập 2: a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm (Hình 18a). Tính độ dài đoạn thẳng EF...
Bài 7 trang 71 Toán 8 Tập 2: Trong Hình 19, cho biết MN // BC, MB // AC...
Bài 8 trang 72 Toán 8 Tập 2: a) Trong Hình 20a, cho biết , MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a...
Bài 9 trang 72 Toán 8 Tập 2: a) Trong Hình 21a, cho biết , OH = 6 cm và HE = 4 cm. Tính độ dài đoạn thẳng HP...
Bài 10 trang 72 Toán 8 Tập 2: Đường đi và khoảng cách từ nhà anh Thanh (điểm M) đến công ty (điểm N) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà của anh Thanh đến công ty...