Với lời giải SBT Toán 11 trang 68 Tập 1 chi tiết trong Bài 1: Giới hạn của dãy số sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 1: Giới hạn của dãy số
Bài 1 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai?
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Vì limqn = 0 với |q| < 1 nên ta có:
do 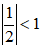
do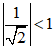
do 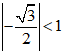
Vậy các đáp án A, C, D đúng.
Vì 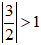
Bài 2 trang 68 SBT Toán 11 Tập 1: Cho limun = a, lim vn = b. Phát biểu nào sau đây là sai?
A. lim(un + vn) = a + b.
B. lim(un – vn) = a – b.
C. lim(un . vn) = a . b.
D. .
Lời giải:
Đáp án đúng là: D
Theo định lí về giới hạn hữu hạn thì ta thấy đáp án D sai.
Bài 3 trang 68 SBT Toán 11 Tập 1: Nếu limun = C và limvn = +∞ (hoặc limvn = −∞) thì bằng:
A. 0.
B. –∞.
C. +∞.
D. –∞ hoặc +∞.
Lời giải:
Đáp án đúng là: A
Nếu limun = C và limvn = +∞ (hoặc limvn = −∞) thì .
Bài 4 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai?
A. Nếu limun = +∞ và limvn = C, C > 0 thì lim = +∞.
B. Nếu limun = −∞ và limvn = C, C < 0 thì lim = +∞.
C. Nếu limun = +∞ và limvn = C, C < 0 thì lim = 0.
D. Nếu limun = –∞ và limvn = C, C > 0 thì .
Lời giải:
Đáp án đúng là: C
Theo định lí giữa giới hạn hữu hạn và giới hạn vô cực, nếu limun = +∞ và limvn = C, C < 0 thì lim = –∞ nên đáp án C sai.
Bài 5 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng?
A. Nếu limun = a thì .
B. Nếu limun = a thì a ≥ 0 và .
C. Nếu limun = a thì a ≥ 0.
D. Nếu un ≥ 0 với mọi n và limun = a thì a ≥ 0 và .
Lời giải:
Đáp án đúng là: D
Theo định lí về giới hạn hữu hạn, nếu un ≥ 0 với mọi n và limun = a thì a ≥ 0 và .
Bài 6 trang 68 SBT Toán 11 Tập 1: Chứng minh rằng .
Lời giải:
Xét dãy số (un) có .
Giả sử h là số dương bé tùy ý cho trước. Ta có:
Do đó, 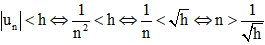
Vậy với các số tự nhiên n lớn hơn thì |un| < h.
Suy ra .
Bài 7 trang 68 SBT Toán 11 Tập 1: Cho hai dãy số (un), (vn) với , . Tính:
a) limun, limvn;
b) lim(un + vn), lim(un – vn), lim(un . vn), .
Lời giải:
a) Ta có
;
.
b) Ta có
lim(un + vn) = limun + limvn = 3 + 8 = 11;
lim(un – vn) = limun – limvn = 3 – 8 = – 5;
lim(un . vn) = limun . limvn = 3 . 8 = 24;
.
Bài 8 trang 68 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ;
b) ;
c) ;
d) .
Lời giải:
a) Vì lim(4n + 2) =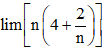
Do đó, .
b) Vì lim(3n + 4) 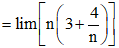
và < 0.
Do đó, .
c) Vì và lim5n = +∞.
Nên .
d)
.
Xem thêm lời giải sách bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai?...
Bài 2 trang 68 SBT Toán 11 Tập 1: Cho limun = a, lim vn = b. Phát biểu nào sau đây là sai?...
Bài 3 trang 68 SBT Toán 11 Tập 1: Nếu limun = C và limvn = +∞ (hoặc limvn = −∞) thì bằng:...
Bài 4 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai?...
Bài 5 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng? ...
Bài 6 trang 68 SBT Toán 11 Tập 1: Chứng minh rằng ....
Bài 7 trang 68 SBT Toán 11 Tập 1: Cho hai dãy số (un), (vn) với , . Tính:...
Bài 8 trang 68 SBT Toán 11 Tập 1: Tính các giới hạn sau:...
Bài 9 trang 69 SBT Toán 11 Tập 1: Tính các giới hạn sau:.....
Bài 10 trang 69 SBT Toán 11 Tập 1: a) Tính tổng của cấp số nhân lùi vô hạn (un) với ......
Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác: