Với lời giải SBT Toán 11 trang 55 Tập 1 chi tiết trong Bài 3: Cấp số nhân sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 3: Cấp số nhân

Bài 31 trang 55 SBT Toán 11 Tập 1: Trong các dãy số (u_n) với số hạng tổng quát sau, dãy số nào là cấp số nhân?

A. u_n = 5ⁿ.

B. u_n = 1 + 5n.

C. u_n = 5ⁿ + 1.

D. u_n = 5 + n².

Lời giải:

Đáp án đúng là: A

Xét từng đáp án, ta thấy dãy số (u_n) với số hạng tổng quát u_n = 5ⁿ là một cấp số nhân.

Thật vậy, ta thấy u_n ≠ 0 với mọi n ∈ ℕ^*.

Ta có: u₁ = 5¹ = 5; $\frac{u_n}{u_{n-1}}=\frac{5^n}{5^{n-1}}=\frac{5^n}{\frac{5^n}{5}}=5$  không đổi với mọi n ∈ ℕ^*.

Vậy dãy số (u_n) với số hạng tổng quát u_n = 5ⁿ là một cấp số nhân với số hạng đầu u₁ = 5 và công bội q = 5.

Bài 32 trang 55 SBT Toán 11 Tập 1: Cho cấp số nhân (u_n) có số hạng đầu u₁ = 2 và công bội q = – 2. Giá trị u₅ là:

A. – 32.

B. – 16.

C. – 6.

D. 32.

Lời giải:

Đáp án đúng là: D

Ta có: u₅ = u₁ . q^{5 – 1} = u₁ . q⁴ = 2 . (– 2)⁴ = 32. 

Bài 33 trang 55 SBT Toán 11 Tập 1: Viết bốn số hạng xen giữa các số 1 và – 243 để được một cấp số nhân có 6 số hạng. Bốn số hạng đó lần lượt là:

A. – 3; – 9; – 27; – 81.

B. 3; – 9; 27; – 81.

C. 3; 9; 27; 81.

D. – 3; 9; – 27; 81.

Lời giải:

Đáp án đúng là: D

Giả sử cấp số nhân có số hạng đầu u₁ = 1, công bội q, bốn số hạng xen giữa 1 và – 243 lần lượt là u₂, u₃, u₄, u₅; và số hạng thứ 6 là u₆ = – 243.

Ta có u₆ = u₁ . q⁵ = q⁵ = – 243 = (– 3)⁵, suy ra q = – 3.

Do đó, bốn số hạng cần tìm lần lượt là: u₂ = u₁ . q = 1 . (– 3) = – 3;

u₃ = u₂ . q = (– 3) . (– 3) = 9;

u₄ = u₃ . q = 9 . (– 3) = – 27;

u₅ = u₄ . q = (– 27) . (– 3) = 81.

Bài 34 trang 55 SBT Toán 11 Tập 1: Cho cấp số nhân (u_n), biết u₂ . u₆ = 64. Giá trị của u₃ . u₅ là

A. – 8.

B. – 64.

C. 64.

D. 8.

Lời giải:

Đáp án đúng là: C

Giả sử công bội của cấp số nhân là q.

Khi đó ta có u₂ . u₆ = (u₁ . q) . (u₁ . q⁵) = $u_1^2.q^6$.

Và $u_3.u_5=\left(u_1.q^2\right).\left(u_1.q^4\right)=u_1^2.q^6$.

Do đó, u₃ . u₅ = u₂ . u₆ = 64.

Bài 35 trang 55 SBT Toán 11 Tập 1: Cho (u_n) là cấp số nhân có $u_1=\frac{1}{3}$ ; u₈ = 729.

Tổng 8 số hạng đầu của cấp số nhân đó là:

A. $\frac{1-3^8}{2}$ .

B. $\frac{3^8-1}{6}$ .

C. $\frac{3^8-1}{2}$ .

D. $\frac{1-3^8}{6}$ .

Lời giải:

Đáp án đúng là: B

Giả sử công bội của cấp số nhân là q.

Khi đó ta có u₈ = u₁ . q⁷ = $\frac{q^7}{3}$ . Mà u₈ = 729 nên $\frac{q^7}{3}=729\Rightarrow q^7=2187$ .

Vì 2 187 = 3⁷, suy ra q = 3.

Vậy tổng 8 số hạng đầu của cấp số nhân đó là:

$S_8=\frac{u_1\left(1-q^8\right)}{1-q}=\frac{\frac{1}{3}.\left(1-3^8\right)}{1-3}=\frac{3^8-1}{6}$.

Bài 36 trang 55 SBT Toán 11 Tập 1: Cho hình vuông C₁ có cạnh bằng 1. Gọi C₂ là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông C₁; C₃ là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông C₂; ... Cứ tiếp tục quá trình như trên, ta được dãy các hình vuông C₁; C₂; C₃; ...; C_n; ... Diện tích của hình vuông C₂₀₂₃ là:

A. $\frac{1}{2^{2022}}$ .

B. $\frac{1}{2^{2023}}$ .

C. $\frac{1}{2^{1011}}$ .

D. $\frac{1}{2^{1012}}$ .

Lời giải:

Đáp án đúng là: A

Hình vuông C₁ có diện tích S₁ = 1.

Hình vuông C₂ là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông C₁, do đó hình vuông C₂ có diện tích S₂ = $\frac{1}{2}{S}_1=\frac{1}{2}$ .

Tương tự, hình vuông C₃ có diện tích $S_3=\frac{1}{2}{S}_2=\frac{1}{2}.\frac{1}{2}=\frac{1}{2^2}$ .

Cứ tiếp tục như thế ta tính được diện tích hình vuông C₂₀₂₃ là $S_{2023}=\frac{1}{2^{2022}}$ .

Bài 37 trang 55 SBT Toán 11 Tập 1: Cho ba số $\frac{2}{b-a},\frac{1}{b},\frac{2}{b-c}$  theo thứ tự lập thành một cấp số cộng. Chứng minh rằng ba số a, b, c theo thứ tự đó lập thành một cấp số nhân.

Lời giải:

Do ba số $\frac{2}{b-a},\frac{1}{b},\frac{2}{b-c}$  theo thứ tự lập thành một cấp số cộng nên

$\frac{1}{b}-\frac{2}{b-a}=\frac{2}{b-c}-\frac{1}{b}$

$\iff \frac{b-a-2b}{b\left(b-a\right)}=\frac{2b-\left(b-c\right)}{b\left(b-c\right)}$

$\iff \frac{-a-b}{b-a}=\frac{b+c}{b-c}$ (do b ≠ 0)

$\Rightarrow \left(-a-b\right)\left(b-c\right)=\left(b-a\right)\left(b+c\right)$

⇔ – ab + ac – b² + bc = b² + bc – ab – ac

⇔ ac – b² = b² – ac

⇔ 2b² = 2ac

⇔ b² = ac

$\iff \frac{b}{a}=\frac{c}{b}$.

Suy ra ba số a, b, c theo thứ tự lập thành một cấp số nhân.  

Bài 38 trang 55 SBT Toán 11 Tập 1: Tìm x để ba số 2x – 3; x; 2x + 3 theo thứ tự lập thành một cấp số nhân.

Lời giải:

Ba số 2x – 3; x; 2x + 3 theo thứ tự lập thành một cấp số nhân khi

$\frac{x}{2x-3}=\frac{2x+3}{x}$

⇒ x² = (2x – 3)(2x + 3)

⇔ x² = 4x² – 9

⇔ 3x² = 9

⇔ x² = 3

$\iff x=\pm \sqrt{3}$.

Vậy $x=\pm \sqrt{3}$  thì thỏa mãn yêu cầu bài toán. 

Bài 39 trang 55 SBT Toán 11 Tập 1: Tìm số hạng đầu và công bội của cấp số nhân (u_n), biết:

Lời giải:

a) Ta có u₂ + u₄ = $\frac{u_3}{q}+u_{3}q=\frac{16}{q}+16q$ .

Mà u₂ + u₄ = 40 nên ⇒ 16 + 16q² = 40q

⇔ 2q² – 5q + 2 = 0  .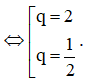

Lại có u₃ = u₁ q² = 16, suy ra u₁ = $\frac{16}{q^2}$ .

Với  thì $u_1=\frac{16}{{\left(\frac{1}{2}\right)}^2}=64$ .

Với q = 2 thì $u_1=\frac{16}{2^2}=4$ .

Vậy u₁ = 64, q = $\frac{1}{2}$  hoặc u₁ = 4, q = 2.

b) Ta có u₁ + u₆ = u₁ + u₁ . q⁵ = 244, suy ra u₁ . q⁵ = 244 – u₁.

Lại có u₂ . u₅ = (u₁ . q) . (u₁ . q⁴) = u₁ . (u₁ . q⁵) = u₁ . (244 – u₁) = 244u₁ – u₁².

Suy ra 244u₁ – u₁² = 243  .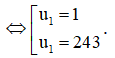

Với u₁ = 1 thì q⁵ = 244 – 1 = 243 = 3⁵, suy ra q = 3.

Với u₁ = 243 thì 243q⁵ = 244 – 243 ⇔ 243q⁵ = 1 $\iff q^5=\frac{1}{243}\iff q^5={\left(\frac{1}{3}\right)}^5$ $\iff q=\frac{1}{3}$ .

Vậy u₁ = 1, q = 3 hoặc u₁ = 243, $q=\frac{1}{3}$ .

c) Ta có 

Lấy (2) chia vế theo vế cho 1, ta được q³ = 27, suy ra q = 3.

Ta có u₁ (1 + 3 + 3²) = 13 ⇔ 13u₁ = 13 ⇔ u₁ = 1.

Vậy u₁ = 1, q = 3.  

Bài 40 trang 55 SBT Toán 11 Tập 1: Cho (u_n) là cấp số nhân có u₁ + u₅ = 51 và u₂ + u₆ = 102.

a) Tính u₁₀.

b) Số 192 là số hạng thứ mấy của cấp số nhân trên?

c) Số 9 216 có là số hạng nào của cấp số nhân trên không?

Lời giải:

a) Xét số hạng đầu u₁ và công bội q. Ta có:

Lấy (2) chia vế theo vế (1) ta được q = 2.

Suy ra u₁ . (1 + 2⁴) = 51 ⇔ 17u₁ = 51 ⇔ u₁ = 3. 

Do đó, u₁₀ = u₁ . q⁹ = 3 . 2⁹ = 1 536.

b) Giả sử số 192 là số hạng thứ k của cấp số nhân (u_n).

Ta có u_k = u₁ . q^{k – 1} = 3  . 2^{k – 1} = 3 . 2^k . $\frac{1}{2}$  = 192, suy ra 2^k = 128 = 2⁷, suy ra k = 7. 

Vậy số 192 là số hạng thứ 7.

c) Giả sử 9 216 là số hạng thứ n của cấp số nhân (u_n).

Ta có 3 . 2^{n – 1} = 9 216 ⇔ 2^{n – 1} = 3 072.

Do 3 072 chia hết cho 3 mà với n là số nguyên dương thì 2^{n – 1} không chia hết cho 3 nên không tồn tại n thoả mãn.

Vậy số 9 216 không là số hạng nào của (u_n).