Với lời giải SBT Toán 11 trang 74 Tập 1 chi tiết trong Bài tập cuối chương 4 trang 72 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài tập cuối chương 4 trang 72

Bài 4.61 trang 74 SBT Toán 11 Tập 1: Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi M, N, M’, N’ lần lượt là trung điểm của các cạnh AB, CD, A’B’, C’D’.

a) Chứng minh rằng bốn điểm M, N, M’, N’ đồng phẳng và tứ giác MNN’M’ là hình bình hành

b) Giả sử MN không song song với BC. Xác định giao tuyến của hai mặt phẳng (MNN’M’) và (BCC’B’).

Lời giải:

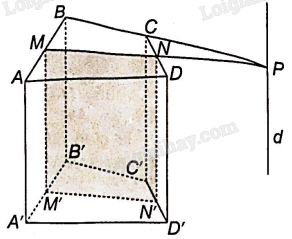
a) Vì M, M’ lần lượt là trung điểm của AB, A’B’ của hình bình hành ABB’A’ nên MM’//AA’ và $M{M}^{\prime }=A{A}^{\prime }$

Tương tự ta có: NN’//DD’ và $N{N}^{\prime }=D{D}^{\prime }$

Tứ giác ADD’A’ là hình bình hành nên AA’//DD’ và $A{A}^{\prime }=D{D}^{\prime }$.

Do đó, $M{M}^{\prime }=N{N}^{\prime }$ và MM’//NN’, suy ra bốn điểm M, N, M’, N’ đồng phẳng và tứ giác MNN’M’ là hình bình hành.

b) Trong mặt phẳng (ABCD), gọi P là giao điểm của hai đường thẳng MN và BC.

Vì BB’// MM’ nên giao tuyến của hai mặt phẳng (MNN’M’) và (BCC’B’) là đường thẳng d qua P và song song với BB’.

Bài 4.62 trang 74 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng và MNPQ là hình bình hành.

Lời giải:

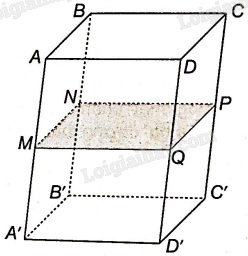
Vì M, N lần lượt là trung điểm của hai cạnh AA’, BB’ của hình bình hành ABB’A’ nên MN//AB, mà AB nằm trong mặt phẳng ABCD nên MN//(ABCD)

Tương tự ta có: NP//(ABCD)

Do đó, (MNP)//(ABCD)

Tương tự ta có: (NPQ)//(ABCD)

Qua N có hai mặt phẳng (MNP) và (NPQ) cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng (MNP) và (NPQ) trùng nhau, tức là bốn điểm M, N, P, Q đồng phẳng.

Chứng minh được: MN//PQ và $MN=PQ\left(=\frac{1}{2}AB\right)$ nên tứ giác MNPQ là hình bình hành.

Bài 4.63 trang 74 SBT Toán 11 Tập 1: Một người thợ đang cố gắng đặt tấm kính ABCD (mép AB không song song với CD) dựa vào tường sao cho mép kính CD song song với đường chân tường, còn mép AB nằm hoàn toàn trên tường. Sau một hồi loay hoay, người thợ vẫn không thể đặt được tấm kính như mong muốn. Hãy giải thích tại sao.

Có cách nào để đặt tấm kính để một mép kính song song với đường chân tường, một mép kính khác nằm hoàn toàn trên tường không?

Lời giải:

Áp dụng định lí ba đường giao tuyến cho ba mặt phẳng gồm: mặt đất, mặt tường và mặt kính. Khi đó ba giao tuyến là mép chân tường và hai mép kính AB, CD. Vì AB không song song với CD nên ba giao tuyến đồng quy, vì vậy, không thể đặt tấm kính sao cho mép CD song song với chân tường.

Có thể dặt tấm kính sao cho mép kính BC nằm trên tường và mép kính AD nằm trên mặt đất. Khi đó, cả hai mép kính đều song song với đường chân tường.