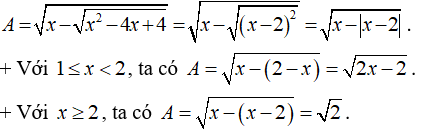Với tóm tắt lý thuyết Toán lớp 9 + tên bài học + hay, chi tiết cùng với bài tập chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 9.

Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức

A. Lý thuyết Căn thức bậc hai và hằng đẳng thức

I. Căn thức bậc hai

1. Định nghĩa

    Với A là một biểu thức đại số, người ta gọi √A là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.

2. Điều kiện có nghĩa(hay có nghĩa) của một căn thức bậc hai

    √A xác định(có nghĩa) ⇔ A ≥ 0

3. Ví dụ cụ thể

-  xác định ⇔ 3x ≥ 0 ⇔ x ≥ 0.

-  xác định ⇔ 3 - 7x ≥ 0 ⇔ x ≤ 3/7.

-  xác định ⇔ 2 - 3x ≥ 0 ⇔ x ≤ 2/3.

-  xác định ⇔ x - 6 ≥ 0 ⇔ x ≥ 6.

-  xác định.

II. Hằng đẳng thức

Muốn khai căn một biểu thức, ta dùng hằng đẳng thức √(A2) = |A|.

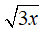
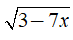
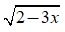
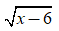
Ví dụ 1: Rút gọn biểu thức 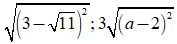 với a < 2

Giải:

Ví dụ 2: Tìm x biết 

Giải:

III. Một số kiến thức cần nhớ

1. Giá trị tuyệt đối

    • Định nghĩa 

    • Hệ quả

     |A| ≥ 0, ∀ A

     |A| = |-A|

     |A| = A ⇔ A ≥ 0; |A| = -A ⇔ A ≤ 0; |A| = 0 ⇔ A = 0

2. Dấu của một tích, một thương

IV. Phương pháp giải toán

DẠNG 1: Tìm điều kiện để một để một căn thức bậc hai xác định.

    • √A xác định (hay có nghĩa) ⇔ A ≥ 0

    • Giải bất phương trình A ≥ 0

    • Kết luận.

DẠNG 2: Khai căn một biểu thức – Tính giá trị một biểu thức chứa căn

    • Khai căn nhờ hằng đẳng thức √(A²) = |A|

    • Rút gọn

DẠNG 3: Phân tích thành nhân tử

    • Viết A ≥ 0 thành (√A)²

    • Sử dụng A² - B² = (A - B)(A + B)

    • Sử dụng A² ± 2AB + B² = (A ± B)²

    • Thêm, bớt tạo thành hằng đẳng thức

DẠNG 4: Giải phương trình

    • Khai căn một biểu thức

    • Giải phương trình chứa dấu giá trị tuyệt đối

B. Bài tập tự luận

Câu 1: Rút gọn các biểu thức sau:

Lời giải

Câu 2: Giải các phương trình sau

Lời giải

Câu 3: Cho biểu thức:

a) Tìm tập xác định của biểu thức.

b) Rút gọn biểu thức A.

Lời giải

a) Điều kiện xác định:

Vậy tập xác định là D = [1; +∞].

b) Ta có: .