Với lời giải SBT Toán 7 trang 10 Tập 1 chi tiết trong Bài 1: Tập hợp Q các số hữu tỉ sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 1: Tập hợp Q các số hữu tỉ
Bài 6 trang 10 SBT Toán 7 Tập 1: Biểu diễn số đối của mỗi số hữu tỉ đã cho trên trục số ở Hình 6.

Lời giải:
Số đối của các số 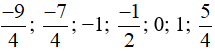 lần lượt là
lần lượt là 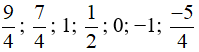
Ta có: .
Chia đoạn thẳng đơn vị thành 4 đoạn thẳng bằng nhau, ta được đơn vị mới bằng đơn vị cũ.
∙ Số hữu tỉ nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 9 đơn vị mới.
∙ Số hữu tỉ nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 7 đơn vị mới.
∙ Số hữu tỉ hay số hữu tỉ nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 2 đơn vị mới.
∙ Số hữu tỉ nằm bên trái điểm 0 và cách điểm 0 một khoảng bằng 5 đơn vị mới.
Vậy biểu diễn số đối của các số 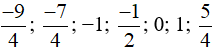 trên trục số như sau:
trên trục số như sau:
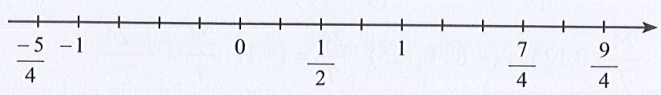
Bài 7 trang 10 SBT Toán 7 Tập 1: So sánh:
a) và 3,2;
b) và −0,01;
c) và −7,112;
d) −943,001 và 943,0001.
Lời giải:
a) và 3,2
Ta có: ; .
Vì 175 < 176 nên hay .
Vậy .
b) và −0,01
Ta có .
Vì 211 < 500 nên
Suy ra hay .
Vậy .
c) và −7,112
Ta có: .
Số đối của −7 và −7,112 lần lượt là 7 và 7,112.
Vì 7 < 7,112 nên −7 > −7,112.
Vậy −7 > −7,112.
d) −943,001 và 943,0001.
Ta có: −943,001 < 0 và 943,0001 > 0.
Vậy −943,001 < 943,0001.
Bài 8 trang 10 SBT Toán 7 Tập 1: Sắp xếp các số sau theo thứ tự tăng dần:
a) ;
b) −5,12; 0,534; −23; 123; 0; 0,543.
Lời giải:
a) Ta có ; .
∙ Nhóm các số lớn hơn 1: .
Ta thấy hai hỗn số có phần nguyên 2 < 3 nên .
∙ Nhóm các số nhỏ hơn 1: .
Vì 15 < 17 nên .
Do đó .
Vậy các số sau theo thứ tự tăng dần là .
b) ∙ Nhóm các số dương: 0,534; 123; 0,543.
Ta có: 0,534 < 0,543 < 123.
∙ Nhóm các số âm: −5,12; −23.
Ta có: −23 < −5,12.
Do đó −23 < −5,12 < 0 < 0,534 < 0,543 < 123.
Vậy các số được sắp xếp theo thứ tự tăng dần: −23; −5,12; 0; 0,534; 0,543; 123.
Bài 9 trang 10 SBT Toán 7 Tập 1: Sắp xếp các số sau theo thứ tự giảm dần:
a) ;
b) .
Lời giải:
a) ∙ Nhóm các phân số dương: .
Ta có: .
Vì 25 > 20 > 4 nên .
Suy ra .
∙ Nhóm các phân số âm: .
Ta có: .
Vì −56 > −63 nên hay .
Do đó .
Vậy các số được sắp xếp theo thứ tự giảm dần: .
b) ∙ Nhóm các số dương: .
Ta thấy: (vì hỗn số có phần nguyên 2 > 1).
(phân số có tử số bé hơn mẫu số); 0,5 < 1.
Ta có: .
Vì 19 < 11 nên hay .
Do đó . (1)
∙ Nhóm các số âm: .
Ta có: .
Vì −0,05 > −0,25 nên . (2)
Từ (1) và (2) suy ra: .
Vậy các số được sắp xếp theo thứ tự giảm dần: .
Bài 10 trang 10 SBT Toán 7 Tập 1: Cho số hữu tỉ (a là số nguyên). Với giá trị nào của a thì:
a) y là số nguyên?
b) y không là số hữu tỉ âm và cũng không là số hữu tỉ dương?
Lời giải:
a) Ta có: 2a – 4 = 2(a – 2).
Với y là số nguyên thì (2a – 4) ⋮ 3 hay 2(a – 2) ⋮ 3.
Vì ƯCLN(2, 3) = 1 nên (a – 2) ⋮ 3 hay a – 2 = 3k (k Î ℤ).
Suy ra a = 3k + 2.
Vậy a là số chia 3 dư 2.
b) Với y không là số hữu tỉ âm và cũng không là số hữu tỉ dương nên y = 0.
Suy ra 2a – 4 = 0 hay a = 2.
Vậy a = 2.
Xem thêm các bài giải sách bài tập Toán 7 Cánh diều hay, chi tiết khác: