Với tóm tắt lý thuyết Toán lớp 6 Bài 7: Hỗn số sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 7: Hỗn số

Video giải Toán 6 Bài 7: Hỗn số – Chân trời sáng tạo

A. Lý thuyết Hỗn số

1. Hỗn số

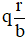Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết  và gọi  là hỗn số.

Ví dụ 1. Cho hai số nguyên dương là 25 và 3; 25 > 3 và 25 không chia hết cho 3.

Thực hiện phép chia 25 cho 3 được thương là 8 và số dư là 1.

Khi đó, 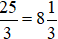. Đọc là “tám, một phần ba”.

Chú ý: Với hỗn số 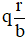 người ta gọi q là phần số nguyên và  là phần phân số của hỗn số.

Ví dụ 2. Viết phân số 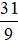 dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.

Lời giải: 

Thực hiện phép chia 31 cho 9 được thương là 3 và số dư là 4.

Khi đó, .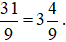

Trong đó, phần số nguyên là 3 và phần phân số là .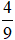

Vậy phân số 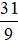 dưới dạng hỗn số là  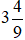và phần số nguyên là 3, phần phân số là .

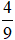2. Đổi hỗn số ra phân số

Ta biết viết phân số 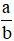 với a > b > 0 thành hỗn số .

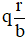Ngược lại, ta đổi được hỗn số 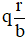 thành phân số, theo quy tắc sau:

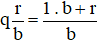
Ví dụ 3. So sánh .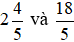

Lời giải:

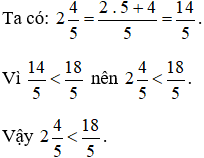
B. Bài tập tự luyện

Bài 1. Viết các hỗn số 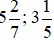 dưới dạng phân số.

Lời giải:

Các hỗn số 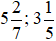 chuyển sang phân số như sau:

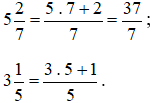
Bài 2. Tính giá trị biểu thức: .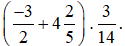

Lời giải:

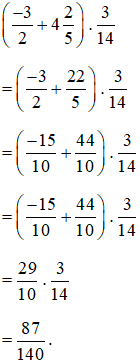
Bài 3. Sắp xếp các độ dài sau theo thứ tự từ nhỏ đến lớn:

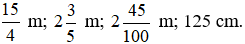
Lời giải:

Đổi: 1 m = 100 cm.

Khi đổi từ m sang cm, ta chia số đó cho 100 (viết dưới dạng phân số).

Khi đó, .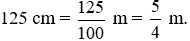

Ta có: .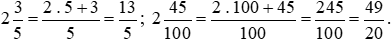

Quy đồng các phân số 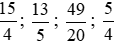, ta thực hiện:

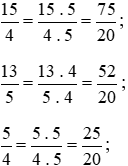
Giữ nguyên phân số .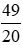

Vì 25 < 49 < 52 < 75 nên .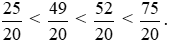

Do đó .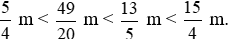

Vậy các độ dài theo thứ tự từ nhỏ đến lớn là:

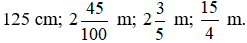
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 6: Giá trị phân số của một số

Lý thuyết Bài 7: Hỗn số

Lý thuyết Bài 1: Số thập phân

Lý thuyết Bài 2: Các phép tính với số thập phân

Lý thuyết Bài 3: Làm tròn số thập phân và ước lượng kết quả