Với giải bài tập Toán lớp 6 Bài 7: Hỗn số chi tiết bám sát nội dung sgk Toán 6 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 7: Hỗn số
Video giải Toán 6 Bài 7: Hỗn số – Chân trời sáng tạo
A. Các câu hỏi trong bài
Giải Toán 6 trang 23 Tập 2 Chân trời sáng tạo
a) Chị An mua 5 phần bánh, được người bán lấy cho một đĩa và một phần, có đúng không?
b) Bà Bé mua 11 phần bánh, được người bán lấy cho hai đĩa và 3 phần, có đúng không?

Lời giải:
a) Người bán lấy một đĩa (4 phần) và một phần.
Do đó, số phần người bán lấy ra là: 4 . 1 + 1 = 5 (phần)
Vậy chị An mua 5 phần, người bán lấy một đĩa và một phần là đúng.
b) Người bán lấy hai đĩa (mỗi đĩa 4 phần) và 3 phần.
Do đó, số phần người bán lấy ra là: 4 . 2 + 3 = 11 (phần)
Vậy bà Bé mua 11 phần, người bán lấy hai đĩa và 3 phần là đúng.
Lời giải:
Lấy a chia b, ta được:
+ Phần số nguyên = Thương;
+ Phần phân số = số dư : số chia = số dư : b.
Ta có: 11 : 2 = 5 dư 1.
Phần số nguyên là: 5
Phần phân số là: 1 : 2 = 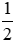 .
.
Vậy phân số 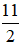 ở dưới dạng hỗn số là
ở dưới dạng hỗn số là 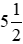 và phần số nguyên là 5, phần phân số là
và phần số nguyên là 5, phần phân số là 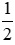 .
.
Giải Toán 6 trang 24 Tập 2 Chân trời sáng tạo
Thực hành 2 trang 24 Toán lớp 6 Tập 2: Tính giá trị của biểu thức 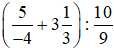 .
.
Lời giải:
Đổi hỗn số ra phân số: 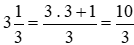 ;
;
Thực hiện phép tính (trong ngoặc trước, ngoài ngoặc sau).
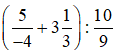
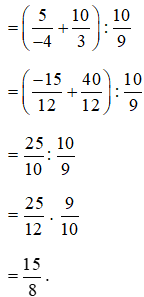
B. Bài tập
Bài 1 trang 24 Toán lớp 6 Tập 2: Dùng hỗn số viết thời gian ở đồng hồ trong các hình vẽ sau:

Thời gian ở hình a có thể viết là 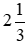 giờ hoặc
giờ hoặc 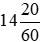 giờ được không?
giờ được không?
Lời giải:
Hỗn số cần tìm gồm:
Phần nguyên = số giờ;
Phần phân số = số phút : 60.
* Hình a đồng hồ chỉ 2 giờ 20 phút (vào buổi sáng) hoặc 14 giờ 20 phút (vào buổi chiều).
- Phần nguyên là 2 hoặc 14;
- Phần phân số là 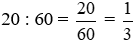
Vậy thời gian trong hình a có thể viết là 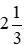 giờ hoặc
giờ hoặc 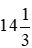 giờ.
giờ.
* Hình b đồng hồ chỉ 4 giờ 50 phút (vào buổi sáng) hoặc 16 giờ 50 phút (vào buổi chiều).
- Phần nguyên là 4 hoặc 16;
- Phần phân số là 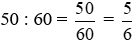
Vậy thời gian trong hình b có thể viết là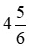 giờ hoặc
giờ hoặc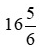 giờ.
giờ.
* Hình c đồng hồ chỉ 6 giờ 10 phút (vào buổi sáng) hoặc 18 giờ 10 phút (vào buổi tối).
- Phần nguyên là 6 hoặc 18;
- Phần phân số là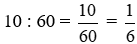
Vậy thời gian trong hình b có thể viết là 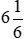 giờ hoặc
giờ hoặc 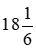 giờ.
giờ.
* Hình đ là 9 giờ 30 phút (vào buổi sáng) hoặc 21 giờ 30 phút (vào buổi tối).
- Phần nguyên là 9 hoặc 21;
- Phần phân số là 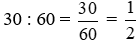
Vậy thời gian trong hình b có thể viết là 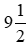 giờ hoặc
giờ hoặc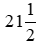 giờ.
giờ.
Thời gian ở hình a có thể viết là 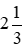 giờ hoặc
giờ hoặc 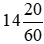 giờ được (vì có phần nguyên là số giờ là 2 giờ sáng hoặc 14 giờ chiều và có phần phân số là
giờ được (vì có phần nguyên là số giờ là 2 giờ sáng hoặc 14 giờ chiều và có phần phân số là 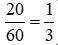 ).
).
Bài 2 trang 24 Toán lớp 6 Tập 2: Sắp xếp các khối lượng sau theo thứ tự từ lớn đến nhỏ:
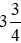 tạ;
tạ; 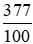 tạ;
tạ; 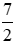 tạ;
tạ; 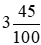 tạ; 365 kg.
tạ; 365 kg.
Lời giải:
Ta có: 1 tạ = 100 kg.
Khi đổi từ kg sang tạ, ta chia số đó cho 100 (viết dưới dạng phân số).
Đổi các phân số, hỗn số sau về phân số có mẫu số bằng 100, ta được:
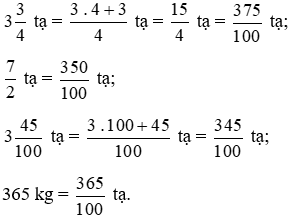
Vì 377 > 375 > 365 > 350 > 345 nên 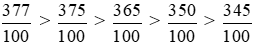 .
.
Do đó .
.
Vậy các khối lượng theo thứ tự từ lớn đến nhỏ là:
 .
.
a) 125 dm2;
b) 218 cm2;
c) 240 dm2;
d) 34 cm2.
Nếu viết chúng theo đề-xi-mét vuông thì sao?
Lời giải:
Các đơn vị đo diện tích sắp xếp theo thứ tự từ lớn đến bé lần lượt là: km2, hm2, dam2, m2, dm2, cm2, mm2. Mỗi đơn vị đo khối lượng đều gấp 100 lần đơn vị bé hơn, liền nó.
Ta có: 1 m2 = 100 dm2, 1 dm2 = 1000 cm2, 1 m2 = 10 000 cm2.
Ta suy ra:
1 dm2 = 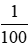 m2;
m2;
1 cm2 = 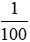 dm2;
dm2;
1 cm2 = 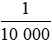 m2.
m2.
Các đại lượng diện tích viết theo mét vuông như sau:
a) 125 dm2 = 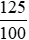 m2 =
m2 = 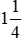 m2;
m2;
b) 218 cm2 = 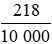 m2 =
m2 = 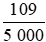 m2;
m2;
c) 240 dm2 = 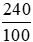 m2 =
m2 = 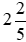 m2;
m2;
d) 34 cm2 = 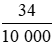 m2 =
m2 = 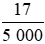 m2.
m2.
Nếu viết chúng theo đề-xi-mét vuông thì ta được:
a) 125 dm2 = 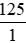 dm2;
dm2;
b) 218 cm2 = 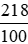 dm2 =
dm2 = 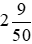 dm2;
dm2;
c) 240 dm2 = 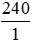 dm2;
dm2;
d) 34 cm2 = 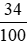 dm2 =
dm2 =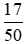 dm2.
dm2.
Lời giải:
Vận tốc mỗi xe = Quãng đường : thời gian mỗi xe đi.
Đổi 70 phút = 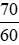 giờ =
giờ = 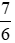 giờ.
giờ.
Vận tốc của xe taxi là:
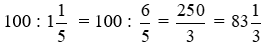 (km/h).
(km/h).
Vận tốc của xe tải là:
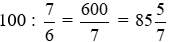 (km/h).
(km/h).
Vì 85 > 83 nên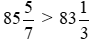 (hỗn số có phần nguyên lớn hơn thì số đó lớn hơn).
(hỗn số có phần nguyên lớn hơn thì số đó lớn hơn).
Vậy vận tốc của xe tải lớn hơn vận tốc xe taxi.
Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Giải SGK Toán 6 Bài 6: Giá trị của một phân số
Giải SGK Toán 6 Bài tập cuối chương 5
Giải SGK Toán 6 Bài 1: Số thập phân
Giải SGK Toán 6 Bài 2: Các phép tính với số thập phân
Lý thuyết Hỗn số
1. Hỗn số
Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết  và gọi
và gọi 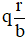 là hỗn số.
là hỗn số.
Ví dụ 1. Cho hai số nguyên dương là 25 và 3; 25 > 3 và 25 không chia hết cho 3.
Thực hiện phép chia 25 cho 3 được thương là 8 và số dư là 1.
Khi đó, 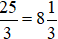 . Đọc là “tám, một phần ba”.
. Đọc là “tám, một phần ba”.
Chú ý: Với hỗn số 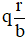 người ta gọi q là phần số nguyên và
người ta gọi q là phần số nguyên và  là phần phân số của hỗn số.
là phần phân số của hỗn số.
Ví dụ 2. Viết phân số 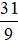 dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.
dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.
Lời giải:
Thực hiện phép chia 31 cho 9 được thương là 3 và số dư là 4.
Khi đó, 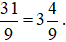 .
.
Trong đó, phần số nguyên là 3 và phần phân số là 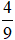 .
.
Vậy phân số 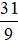 dưới dạng hỗn số là
dưới dạng hỗn số là 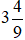 và phần số nguyên là 3, phần phân số là
và phần số nguyên là 3, phần phân số là 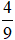 .
.
2. Đổi hỗn số ra phân số
Ta biết viết phân số 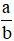 với a > b > 0 thành hỗn số
với a > b > 0 thành hỗn số 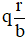 .
.
Ngược lại, ta đổi được hỗn số 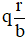 thành phân số, theo quy tắc sau:
thành phân số, theo quy tắc sau:
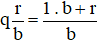
Ví dụ 3. So sánh 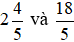 .
.
Lời giải: