Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Hỗn số được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hỗn số. Mời các bạn đón xem:
Bài tập Toán 6 Hỗn số
A. Bài tập Hỗn số
Bài 1. Viết các hỗn số 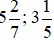 dưới dạng phân số.
dưới dạng phân số.
Lời giải:
Các hỗn số 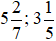 chuyển sang phân số như sau:
chuyển sang phân số như sau:
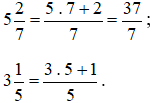
Bài 2. Tính giá trị biểu thức: 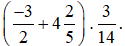 .
.
Lời giải:
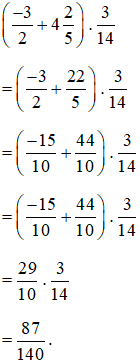
Bài 3. Sắp xếp các độ dài sau theo thứ tự từ nhỏ đến lớn:
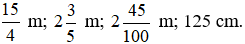
Lời giải:
Đổi: 1 m = 100 cm.
Khi đổi từ m sang cm, ta chia số đó cho 100 (viết dưới dạng phân số).
Khi đó, 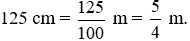 .
.
Ta có: 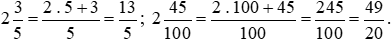 .
.
Quy đồng các phân số 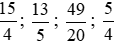 , ta thực hiện:
, ta thực hiện:
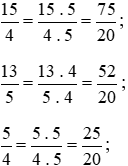
Giữ nguyên phân số 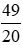 .
.
Vì 25 < 49 < 52 < 75 nên 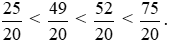 .
.
Do đó 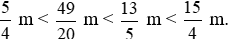 .
.
Vậy các độ dài theo thứ tự từ nhỏ đến lớn là:
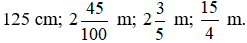
Câu 4: Dùng phân số hoặc hỗn số (nếu có thể) để viết các đại lượng diện tích dưới đây theo mét vuông, ta được:
a) 125dm2b) 218cm2 c) 240dm2 d) 34cm2
A.
B.
C.
D.
Trả lời:
a)
b)
c)
d)
Vậy
Đáp án cần chọn là: A
Câu 5: Hai xe ô tô cùng đi được quãng đường 100 km, xe taxi chạy trong giờ và xe tải chạy trong 70 phút. So sánh vận tốc hai xe.
A.Vận tốc xe tải lớn hơn vận tốc xe taxi
B.Vận tốc xe taxi lớn hơn vận tốc xe tải
C.Vận tốc hai xe bằng nhau
D.Không so sánh được
Trả lời:
Đổi 70 phút = giờ
Vận tốc của xe taxi là:
(km/h)
Vận tốc của xe tải là:
(km/h)
Ta có: nên vận tốc của xe taxi lớn hơn vận tốc xe tải.
Đáp án cần chọn là: B
Câu 6: Viết 2 giờ 15 phút dưới dạng hỗn số với đơn vị là giờ:
A. giờ
B. giờ
C. giờ
D. giờ
Trả lời:
2 giờ 15 phút = giờ
Đáp án cần chọn là: C
Câu 7: Tính
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: C
Câu 8: Tìm x biết
A. x = 1
B. x = 2
C. x = 3
D. x = 4
Trả lời:
Đáp án cần chọn là: A
Câu 9: Viết phân số dưới dạng hỗn số ta được
A.
B.
C.
D.
Trả lời:
Ta có: 4 : 3 bằng 1 (dư 1) nên
Đáp án cần chọn là: D
Câu 10: Hỗn số được viết dưới dạng phân số là
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: B
Câu 11: Chọn câu đúng
A.
B.
C.
D.
Trả lời:
Đáp án A: Nên A sai.
Đáp án B: nên B sai.
Đáp án C: nên C đúng.
Đáp án D: nên D sai.
Đáp án cần chọn là: C
Câu 12: Dùng hỗn số viết thời gian ở đồng hồ trong các hình vẽ, ta được lần lượt các hỗn số là:
A.
B.
C.
D.
Trả lời:
Hình a:
Hình b:
Hình c:
Hình d:
Vậy ta được các hỗn số:
Đáp án cần chọn là: A
Câu 13: Sắp xếp các khối lượng sau theo thứ tự từ lớn đến nhỏ:
tạ; tạ; tạ; tạ; 365 kg.
A. tạ; tạ; 365 kg; tạ; tạ.
B. tạ; tạ; tạ; tạ; 365 kg.
C. tạ; tạ; 365 kg; tạ; tạ.
D. tạ; 365 kg; tạ; tạ; tạ.
Trả lời:
Ta có:
tạ = tạ = tạ
tạ = tạ
tạ = tạ = tạ
365 kg = tạ
=> Các khối lượng theo thứ tự từ lớn đến nhỏ là:
tạ; tạ; 365 kg; tạ; tạ.
Đáp án cần chọn là: C
Câu 14: Kết quả của phép tính bằng
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: B
Câu 15: Giá trị nào dưới đây của x thỏa mãn
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: A
Câu 16: Chọn câu đúng
A.
B.
C.
D.
Trả lời:
Đáp án A: Nên A sai.
Đáp án B: nên B sai.
Đáp án C: Nên C đúng.
Đáp án D: nên D sai.
Đáp án cần chọn là: C
Câu 17: Tính hợp lý ta được
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: B
Câu 18. Giá trị nào dưới đây của x thỏa mãn
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: A
B. Lý thuyết Hỗn số
1. Hỗn số
Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết  và gọi
và gọi 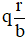 là hỗn số.
là hỗn số.
Ví dụ 1. Cho hai số nguyên dương là 25 và 3; 25 > 3 và 25 không chia hết cho 3.
Thực hiện phép chia 25 cho 3 được thương là 8 và số dư là 1.
Khi đó, 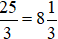 . Đọc là “tám, một phần ba”.
. Đọc là “tám, một phần ba”.
Chú ý: Với hỗn số 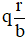 người ta gọi q là phần số nguyên và
người ta gọi q là phần số nguyên và  là phần phân số của hỗn số.
là phần phân số của hỗn số.
Ví dụ 2. Viết phân số 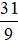 dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.
dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.
Lời giải:
Thực hiện phép chia 31 cho 9 được thương là 3 và số dư là 4.
Khi đó, 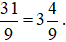 .
.
Trong đó, phần số nguyên là 3 và phần phân số là 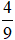 .
.
Vậy phân số 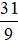 dưới dạng hỗn số là
dưới dạng hỗn số là 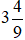 và phần số nguyên là 3, phần phân số là
và phần số nguyên là 3, phần phân số là 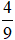 .
.
2. Đổi hỗn số ra phân số
Ta biết viết phân số 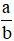 với a > b > 0 thành hỗn số
với a > b > 0 thành hỗn số 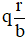 .
.
Ngược lại, ta đổi được hỗn số 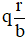 thành phân số, theo quy tắc sau:
thành phân số, theo quy tắc sau:
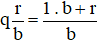
Ví dụ 3. So sánh 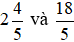 .
.
Lời giải: