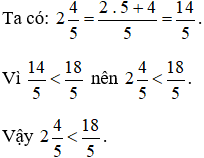Với giải sách bài tập Toán 6 Bài 7: Hỗn số sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 7: Hỗn số

Bài 1 trang 32 sách bài tập Toán lớp 6 Tập 2: Sắp xếp các số sau theo thứ tự tăng dần: .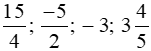

Lời giải:

Để sắp xếp các số trên theo thứ tự tăng dần, ta làm như sau: 

Bước 1: Đưa các số nguyên, hỗn số về dạng phân số.

Bước 2: Phân loại các phân số dương và phân số âm.

Bước 3: So sánh các phân số với nhau trong từng nhóm rồi sắp xếp các số theo thứ tự tăng dần (các phân số âm luôn nhỏ hơn các phân số dương).

- Đưa các số nguyên, hỗn số về dạng phân số: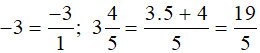 

- Phân loại:

+ Nhóm phân số dương: .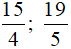

+ Nhóm phân số âm: .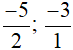

- So sánh các phân số với nhau trong từng nhóm:

+ Nhóm phân số dương:

Ta có: .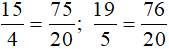

Vì 75 < 76 nên .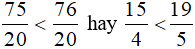

+ Nhóm phân số âm: 

Ta có: .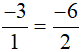

Vì −5 > −6 nên .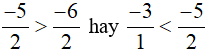

Do đó .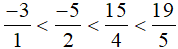

Vậy các số được sắp xếp theo thứ tự tăng dần là: .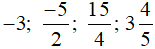

Bài 2 trang 32 sách bài tập Toán lớp 6 Tập 2: Tính:

Lời giải:

Đổi các hỗn số thành phân số, bài toán trở về cộng, trừ, nhân, chia hai phân số.

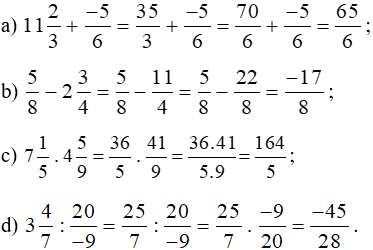
Bài 3 trang 32 sách bài tập Toán lớp 6 Tập 2: So sánh:

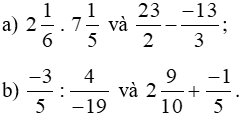
Lời giải:

Đổi các hỗn số thành phân số, bài toán trở về cộng, trừ, nhân, chia hai phân số, sau đó so sánh hai biểu thức vừa tính được.

a)Tính giá trị hai biểu thức trên, ta được:

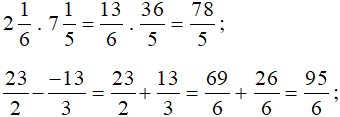
Ta có: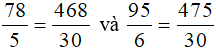 

Vì 468 < 475 nên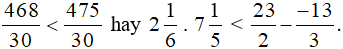 

Vậy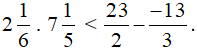 

b)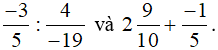 

Tính giá trị hai biểu thức trên, ta được:

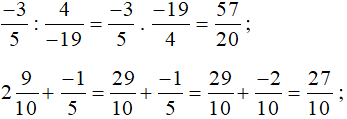
Ta có: .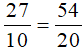

Vì 57 > 54 nên .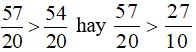

Do đó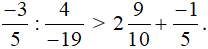  

Vậy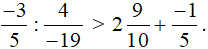 

Bài 4 trang 32 sách bài tập Toán lớp 6 Tập 2: Tìm x biết:

Lời giải:

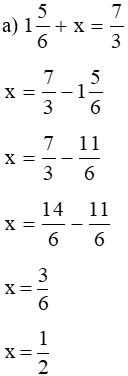
Vậy .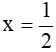

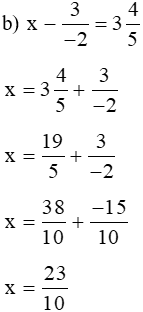
Vậy .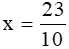

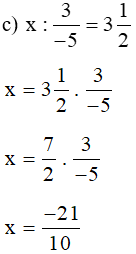
Vậy .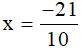

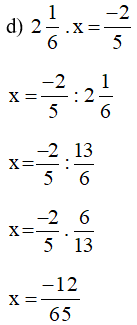
Vậy .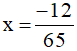

Bài 5 trang 32 sách bài tập Toán lớp 6 Tập 2: Thực hiện phép tính:

Lời giải:

Bài 6 trang 32 sách bài tập Toán lớp 6 Tập 2: Trong một buổi tập bơi, An dành  giờ để khởi động, tự lập là  giờ, nghỉ giữa buổi tập là  giờ và thời gian tập có hướng dẫn của huấn luyện viên là  giờ. Hỏi buổi tập bơi của An kéo dài bao nhiêu giờ? (Viết kết quả bằng phân số và hỗn số).

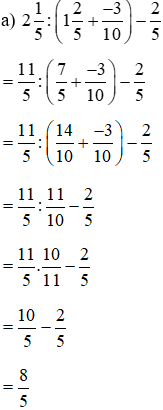
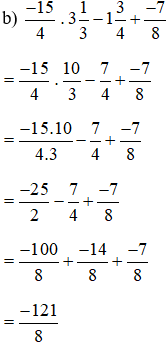
Lời giải:

Buổi tập bơi của An kéo dài: 

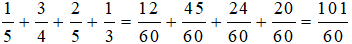(giờ).

Ta có: .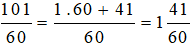

Vậy buổi tập bơi của An kéo dài 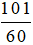 giờ hay  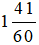giờ.

Bài 7 trang 32 sách bài tập Toán lớp 6 Tập 2: Ô tô chạy với vận tốc trung bình  km/h. Tính quãng đường ô tô chạy được trong  giờ. Cùng quãng đường đó nhưng với vận tốc trung bình là 45 km/h thì thời gian chạy của ô tô là bao nhiêu? (Viết kết quả bằng hỗn số.)

Lời giải:

Ta có: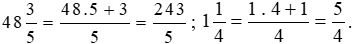 

Quãng đường mà ô tô đi được là:

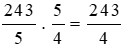(km)

Nếu chạy với vận tốc trung bình là 45 km/h thì thời gian ô tô đi là:

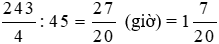 (giờ).

Vậy nếu chạy với vận tốc trung bình là 45 km/h thì thời gian chạy của ô tô là 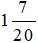 giờ.

Bài 8 trang 33 sách bài tập Toán lớp 6 Tập 2: Hai mảnh đất cùng ở mặt đường có chiều sâu như nhau. Một mảnh có dạng hình vuông cạnh m, mảnh còn lại có dạng hình chữ nhật. Biết diện tích mảnh đất hình vuông bằng  diện tích mảnh đất hình chữ nhật. Mặt tiền mảnh đất hình chữ nhật dài bao nhiêu mét? Diện tích mảnh đất hình chữ nhật bằng bao nhiêu phần diện tích mảnh đất hình vuông?

Lời giải:

Mảnh đất hình vuông:

Mảnh đất hình chữ nhật:

Diện tích mảnh đất hình vuông là:

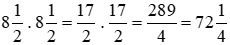(m²)

Diện tích mảnh đất hình chữ nhật là: 

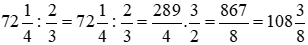(m²)

Chiều dài (hay độ dài mặt tiền) của mảnh đất hình chữ nhật là: 

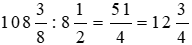(m)

Diện tích mảnh đất hình chữ nhật bằng 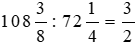 diện tích mảnh đất hình vuông.

Vậy mặt tiền mảnh đất hình chữ nhật dài 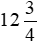m và diện tích mảnh đất hình chữ nhật bằng  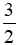diện tích mảnh đất hình vuông.

Lý thuyết Hỗn số

1. Hỗn số

Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết  và gọi 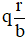 là hỗn số.

Ví dụ 1. Cho hai số nguyên dương là 25 và 3; 25 > 3 và 25 không chia hết cho 3.

Thực hiện phép chia 25 cho 3 được thương là 8 và số dư là 1.

Khi đó, 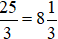. Đọc là “tám, một phần ba”.

Chú ý: Với hỗn số 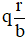 người ta gọi q là phần số nguyên và  là phần phân số của hỗn số.

Ví dụ 2. Viết phân số 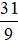 dưới dạng hỗn số và cho biết phần số nguyên, phần phân số.

Lời giải: 

Thực hiện phép chia 31 cho 9 được thương là 3 và số dư là 4.

Khi đó, .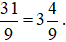

Trong đó, phần số nguyên là 3 và phần phân số là .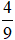

Vậy phân số 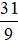 dưới dạng hỗn số là  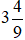và phần số nguyên là 3, phần phân số là .

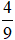2. Đổi hỗn số ra phân số

Ta biết viết phân số 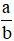 với a > b > 0 thành hỗn số .

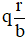Ngược lại, ta đổi được hỗn số 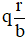 thành phân số, theo quy tắc sau:

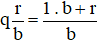
Ví dụ 3. So sánh .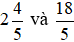

Lời giải: