Với tóm tắt lý thuyết Toán lớp 6 Bài 1: Hình vuông, Tam giác đều, Lục giác đều sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 1: Hình vuông, Tam giác đều, Lục giác đều

Video giải Toán 6 Bài 1: Hình vuông, Tam giác đều, Lục giác đều - Chân trời sáng tạo

A. Lý thuyết Hình vuông, Tam giác đều, Lục giác đều

1. Hình vuông

Hình vuông có:

+ Bốn đỉnh.

+ Bốn cạnh bằng nhau.

+ Bốn góc bằng nhau và bằng góc vuông.

+ Hai đường chéo của hình vuông bằng nhau.

Ví dụ:

Hình vuông ABCD có:

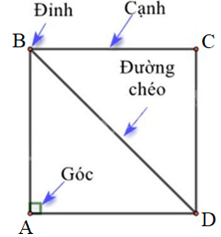
- Bốn đỉnh A, B, C, D.

- Bốn cạnh bằng nhau: AB = BC = CD = DA.

- Bốn góc ở các đỉnh A, B, C, D là góc vuông.

- Hai đường chéo bằng nhau: AC = BD.

Cách vẽ hình vuông

Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng a (cm).

Bước 1: Vẽ đoạn thẳng AB = a (cm).

Bước 2: Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = a (cm).

Bước 3: Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = a (cm).

Bước 4: Nối C với D ta được hình vuông ABCD.

2. Tam giác đều

Tam giác đều có:

+ Ba đỉnh.

+ Ba cạnh bằng nhau.

+ Ba góc ở ba đỉnh bằng nhau.

Ví dụ:

Tam giác đều ABC có:

- Ba đỉnh A, B, C.

- Ba cạnh bằng nhau: AB = BC = CA.

- Ba góc đỉnh A, B, C bằng nhau.

Cách vẽ tam giác đều

Cách vẽ tam giác đều cạnh a (cm) bằng thước và compa:

Bước 1: Dùng thước vẽ đoạn thẳng AB = a (cm).

Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.

Bước 3: Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.

Bước 4: Dùng thước vẽ các đoạn thẳng AC và BC.

Ta được tam giác ABC đều cạnh a (như hình vẽ).

3. Lục giác đều

Hình lục giác đều có sáu đỉnh, sáu cạnh bằng nhau, sáu góc ở các đỉnh bằng nhau, ba đường chéo chính bằng nhau.

Ví dụ:

Lục giác đều ABCDEF có:

- Sáu đỉnh A, B, C, D, E, F.

- Sáu cạnh bằng nhau: AB = BC = CD = DE = EF.

- Sáu góc đỉnh A, B, C, D, E, F bằng nhau.

- Ba đường chéo chính bằng nhau AD = BE = CF.

B. Bài tập tự luyện

Bài 1. Dùng thước và êke để vẽ hình vuông cạnh 8 cm. Kẻ thêm hai đường chéo rồi dùng compa đo và so sánh độ dài của chúng.

Hướng dẫn giải

* Vẽ hình vuông cạnh 8 cm.

- Vẽ cạnh AB = 8 cm.

- Vẽ đường thẳng qua A vuông góc với AB. Trên đường thẳng này lấy điểm D sao cho AD = 8 cm.

- Vẽ đường thẳng qua B vuông góc với AB. Trên đường thẳng này lấy điểm C sao cho BC = 7cm.

- Nối C với D ta được hình vuông ABCD.

* Đo và so sánh độ dài hai đường chéo của hình vuông ABCD.

- Nối A với C, B với D. Khi đó, AC và BD là hai đường chéo của hình vuông ABCD.

- Mở compa một đoạn bằng AC và giữ nguyên compa.

- Đặt một đầu của compa trùng với một trong hai điểm của đoạn thẳng BD, ta thấy điểm còn lại trùng với đầu kia của compa.

Do đó hai đường chéo của hình vuông ABCD bằng nhau.

Bài 2. Dùng thước và compa để vẽ hình tam giác đều cạnh 5 cm.

Hướng dẫn giải

Bước 1: Vẽ đoạn thẳng BC = 5 cm.

Bước 2: Vẽ đường tròn tâm C bán kính 5 cm và đường tròn tâm B bán kính 5 cm. 

Bước 3: Gọi A là một trong hai giao điểm của đường tròn. 

Khi đó ta có: AB = AC = BC = 5 cm, các góc của tam giác ABC bằng nhau.

Ta được tam giác đều ABC cạnh 5 cm.

Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 4: Phép nhân và phép chia hết hai số nguyên

Lý thuyết Bài 1: Hình vuông, Tam giác đều, Lục giác đều

Lý thuyết Bài 2: Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân

Lý thuyết Bài 3: Chu vi và diện tích của một số hình trong thực tiễn

Lý thuyết Bài 1: Thu thập và phân loại dữ liệu