Với tóm tắt lý thuyết Toán lớp 6 Bài 3: Chu vi và diện tích của một số hình trong thực tiễn sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 3: Chu vi và diện tích của một số hình trong thực tiễn

Video giải Toán 6 Bài 3: Chu vi và diện tích của một số hình trong thực tiễn - Chân trời sáng tạo

A. Lý thuyết Chu vi và diện tích của một số hình trong thực tiễn

1. Chu vi và diện tích hình chữ nhật

Cho hình chữ nhật có chiều dài là a, chiều rộng là b (như hình vẽ).

Chu vi của hình chữ nhật là: P = (a + b) . 2

Diện tích của hình chữ nhật là: S = a . b

Ví dụ: Cho hình chữ nhật EFGH có EF = GH = 6 cm; EH = FG = 3 cm. Tính chu vi và diện tích hình chữ nhật EFGH.

Hướng dẫn giải

Chu vi hình chữ nhật EFGH là:

(6 + 3) . 2 = 18 (cm)

Diện tích hình chữ nhật EFGH là:

6 . 3 = 18 (cm²).

Vậy hình chữ nhật EFGH có chu vi là 18 cm và diện tích là 18 cm².

2. Chu vi và diện tích của hình vuông

Cho hình vuông có độ dài một cạnh bằng a (như hình vẽ).

Chu vi hình vuông là: P = 4a.

Diện tích hình vuông là: S = a . a = a².

Ví dụ: Một mảnh ruộng hình vuông có cạnh bằng 15m. Năng suất lúa là 0,9 kg/m². Tính sản lượng thu hoạch được trên mảnh ruộng hình vuông.

Hướng dẫn giải

Diện tích mảnh ruộng hình vuông là:

15² = 225 (m²).

Sản lượng thu hoạch được là:

225 : 0,9 = 312,5 (kg).

Vậy sản lượng thu hoạch được trên mảnh ruộng hình vuông là 312,5 kg.

3. Chu vi và diện tích của hình tam giác

Cho tam giác có độ dài ba cạnh lần lượt là a, b, c và chiều cao tương ứng với cạnh a có độ dài là h (như hình vẽ).

Chu vi hình hình tam giác là: P = a + b + c.

Diện tích hình tam giác là: 

Ví dụ: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm, BC = 5 cm. Tính chu vi và diện tích tam giác ABC.

Hướng dẫn giải

Chu vi tam giác ABC là:

3 + 4 + 5 = 12 (cm).

Diện tích tam giác ABC là:

Vậy tam giác ABC có chu vi là 12 cm và diện tích là 6 cm².

4. Chu vi và diện tích của hình thang

Cho hình thang có độ dài bốn cạnh là a, b, c, d và đường cao h (như hình vẽ).

Chu vi của hình thang là: P = a + b + c + d

Diện tích của hình thang là:

Ví dụ: Tính diện tích hình thang cân có độ dài hai đáy là 5 m và 3,5 m; chiều cao là 4 m.

Hướng dẫn giải

Diện tích hình thang cân là:

Vậy diện tích hình thang cân là 17 cm².

5. Chu vi và diện tích hình bình hành

Cho hình bình hành có độ dài hai cạnh là a và b, chiều cao tương ứng với một cạnh a có độ dài là h (như hình vẽ).

Chu vi hình bình hành là: P = 2(a + b).

Diện tích hình bình hành là: S = a . h.

Ví dụ: Hình bình hành có độ dài một cạnh là 12 cm và chiều cao tương ứng là 8 cm.

Khi đó, diện tích của hình bình hành là:

12 . 8 = 96 (cm²).

6. Chu vi và diện tích hình thoi

Cho hình thoi có độ dài một cạnh là a, độ dài hai đường chéo của hình thoi là m và n.

Chu vi của hình thoi là: P = 4a.

Diện tích của hình thoi là: 

Ví dụ: Hình thoi có độ dài hai đường chéo là 60 m và 50 m có diện tích là:

6. Chu vi và diện tích của một số hình trong thực tiễn

a) Tính chu vi của một số hình trong thực tiễn:

Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó.

b) Tính diện tích của một số hình trong thực tiễn:

− Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, … thì ta áp dụng công thức và tính.

− Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, …

Ví dụ: Tính chu vi và diện tích hình được tô màu sau:

Hướng dẫn giải

Chu vi của hình đã cho là:

8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).

Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:

Diện tích hình chữ nhật to là: 

5 . 7 = 35 (cm²).

Diện tích hình chữ nhật nhỏ là: 

8 . (7 – 6) = 8 (cm²).

Diện tích hình ban đầu là: 

35 + 8 = 43 (cm²).

Vậy hình được tô màu có chu vi là 40 cm và diện tích là 43 cm².

B. Bài tập tự luyện

Bài 1. Cho hình thang MNPQ có diện tích là 60 cm², MQ = 6 cm, NP = 9 cm. Kẻ đường cao MH và tính độ dài của đường cao đó.

Hướng dẫn giải

Kẻ đường cao MH của hình thang MNPQ (như hình vẽ).

Diện tích hình thang là:

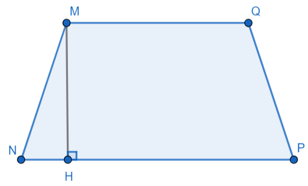
Vậy độ dài đường cao MH bằng 8 cm.

Bài 2. Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Loại gạch lát nền được sử dụng là gạch hình chữ nhật có chiều dài 20 cm, chiều rộng 50 cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể)?

Hướng dẫn giải

Diện tích căn phòng hình chữ nhật là:

8 . 6 = 48 (m²)

Diện tích của một viên gạch hình chữ nhật là:

20 . 50 = 1 000 (cm²) = 0,1 (m²).

Số viên gạch bác Khôi cần dùng là:

48 : 0,1 = 480 (viên).

Vậy để lát nền căn phòng hình chữ nhật, bác Khôi phải sử dụng 480 viên gạch.

Bài 3. Người ta cần xây tường rào và lát cỏ cho một khu vui chơi như hình dưới đây. Chi phí xây tường rào mỗi mét tường tốn 150 000 đồng, còn chi phí lát cỏ mỗi mét vuông tốn 100 000 đồng. Tính tổng số tiền cần để xây tường rào và lát cỏ cho một khu vui chơi.

Hướng dẫn giải

Ta lấy các điểm A, B, C, D, E, F, G, H (như hình vẽ).

Độ dài cạnh AH là:

AH = BC + DE + FG = 4 + 4 + 4 = 12 (cm).

Vì người ta xây tường rào xung quanh khu vườn, nên số mét tường rào chính là chu vi của khu vườn. 

Chu vi khu vui chơi là:

AB + BC + DE + EF + FG + GH + AH

= 12 + 4 + 4 + 4 + 4 + 4 + 4 + 12 + 12

= 12 . 3 + 4 . 6 = 36 + 24 = 60 (m).

Số tiền để xây tường rào cho khu vui chơi là:

150 000 . 60 = 9 000 000 (đồng).

Diện tích khu vui chơi bằng tổng của hình vuông ABGH có cạnh bằng 12 cm và hình vuông CDEF có cạnh bằng 4 m.

Diện tích hình vuông ABGH là:

12² = 144 (m²).

Diện tích hình vuông CDEF là:

4² = 16 (m²).

Diện tích khu vui chơi là:

144 + 16 = 160 (m²).

Số tiền để lát cỏ cho khu vui chơi là:

100 000 . 160 = 16 000 000 (đồng).

Tổng số tiền cần để xây tường rào và lát cỏ cho một khu vui chơi là:

9 000 000 + 16 000 000 = 25 000 000 (đồng).

Vậy tổng số tiền cần để xây tường rào và lát cỏ cho một khu vui chơi là 25 000 000 đồng.

Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân

Lý thuyết Bài 3: Chu vi và diện tích của một số hình trong thực tiễn

Lý thuyết Bài 1: Thu thập và phân loại dữ liệu

Lý thuyết Bài 2: Biểu diễn dữ liệu trên bảng

Lý thuyết Bài 3: Biểu đồ tranh