Với giải sách bài tập Toán 6 Bài 1: Hình vuông - Tam giác đều - Lục giác đều sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 1: Hình vuông - Tam giác đều - Lục giác đều
Lời giải:
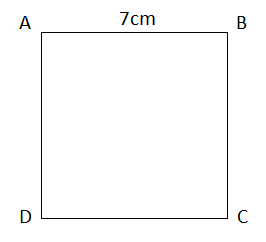
Vì ABCD là hình vuông nên AB = BC = CD = DA = 7 cm.
Vậy BC = CD = DA = 7 cm.
Lời giải:
- Dùng thước thẳng vẽ đoạn thẳng AB = 5 cm:
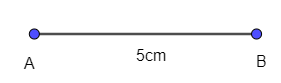
- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B.
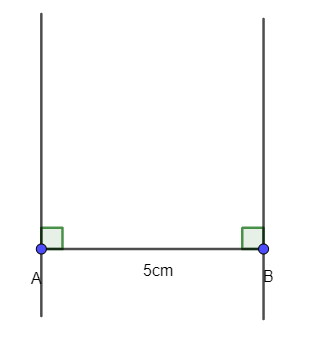
- Trên đường vuông góc tại A lấy điểm D với AD = 5 cm. Trên đường vuông góc tại B lấy điểm C với BC = 5cm
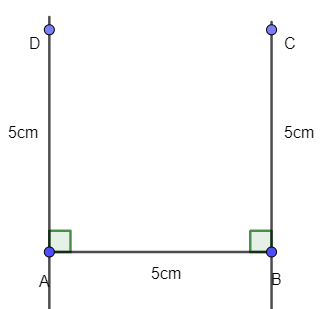
- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài là 5 cm:
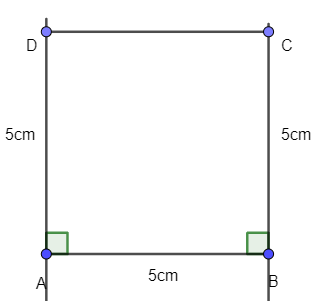
Lời giải:
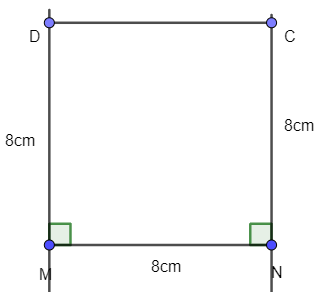
- Dùng thước thẳng vẽ đoạn thẳng MN = 5 cm:
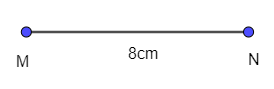
- Dùng eke và thước vẽ các đường thẳng vuông góc với MN tại M và N.
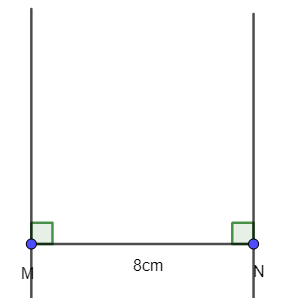
- Trên đường vuông góc tại M lấy điểm D với MD = 8 cm. Trên đường vuông góc tại N lấy điểm C với NC = 8cm
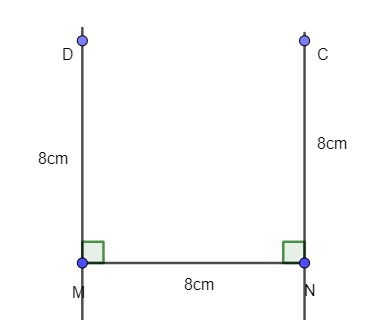
- Kẻ đoạn thẳng nối C và D ta được tứ giác MNCD là hình vuông có độ dài là 8 cm:
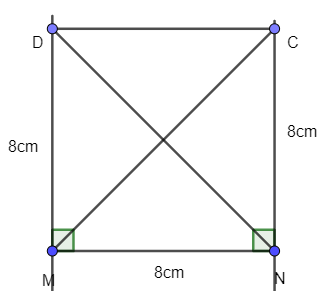
Ta mở compa tâm M bán kính MC, giữ nguyên bán kính đó, đặt một đầu vào điểm N ta thấy đầu còn lại trùng với điểm D.
Do đó hai đường chéo của hình vuông bằng nhau.
Lời giải:
Vì tam giác MNP đều nên MN = NP = MP = 3 cm.
Vậy MN = NP = 3cm.
Lời giải:
- Dùng thước vẽ đoạn thẳng AB = 6cm:
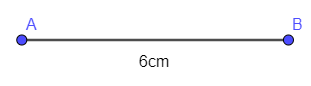
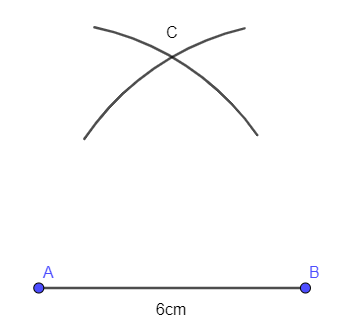
- Dùng compa vẽ các phần đường tròn cùng bán kính 4 cm và có tâm lần lượt là A, B:
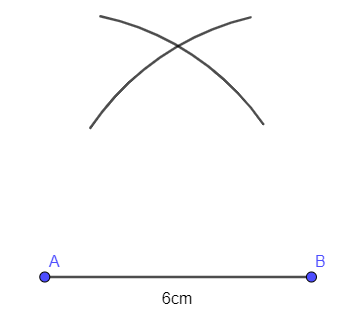
- Hai phần đường tròn nói trên cắt nhau tại điểm C:
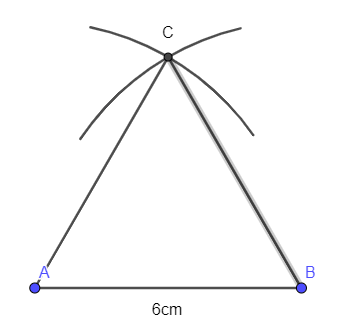
- Kẻ đoạn thẳng nối C và A, C và B ta có tam giác đều ABC với cạnh 6 cm:
Lời giải:
+) Vẽ hình vuông có cạnh 4cm:
- Dùng thước thẳng vẽ đoạn thẳng AB = 4 cm:
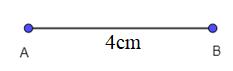
- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B.
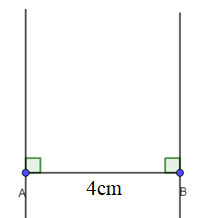
- Trên đường vuông góc tại A lấy điểm D với AD = 5 cm. Trên đường vuông góc tại B lấy điểm C với BC = 5cm
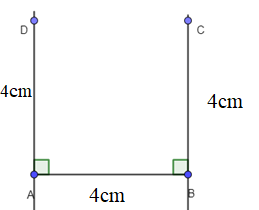
- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài là 5 cm:
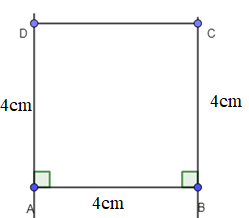
Sau đó tẩy xóa các phần thừa đi ta được hình vuông ABCD:
+) Vẽ 4 tam giác đều cạnh 4cm
Xoay các cung tròn tâm A, B, C, D bán kính 4cm, ta được hình vẽ sau:
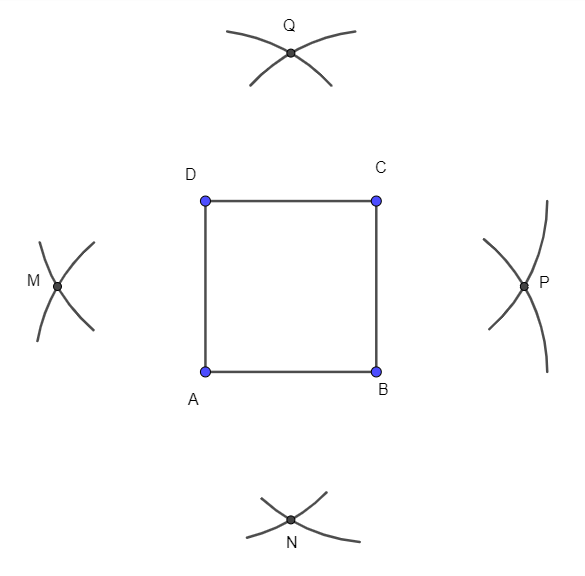
Nối A với M, A với N, B với N, B với P, C với P, C với Q, D với Q và D với M:
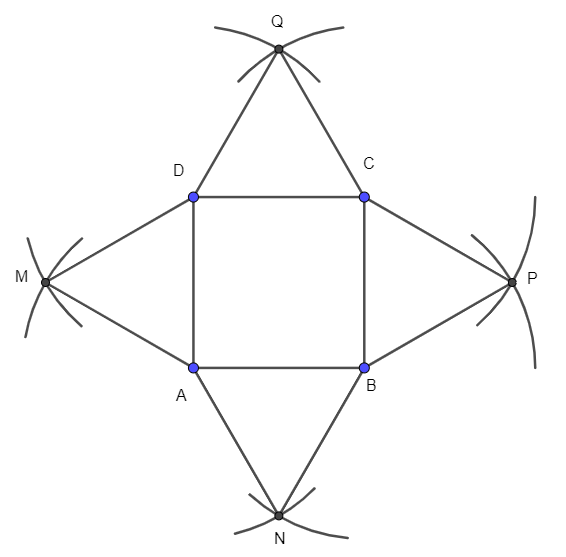
Sau đó xóa đi các nét thừa ta được hình cần vẽ:
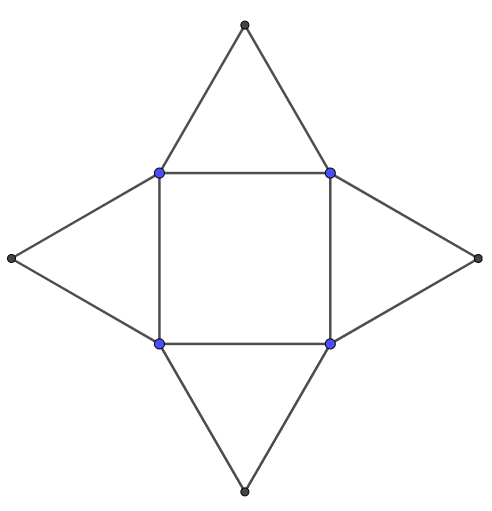
Các em làm như sau để xếp thành bao thư:
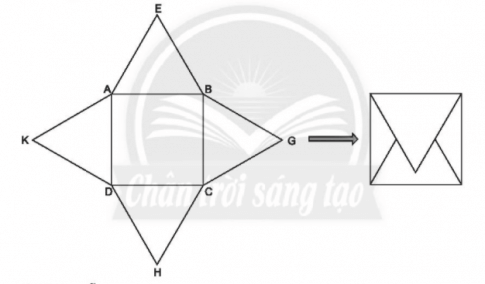
Lời giải:
Ta có 6 hình tam giác đều thì ghép như sau, ta được hình lục giác đều:
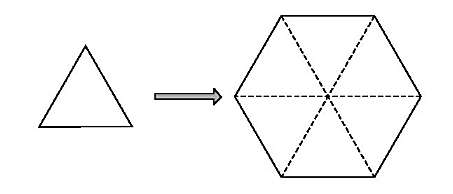
Lời giải:
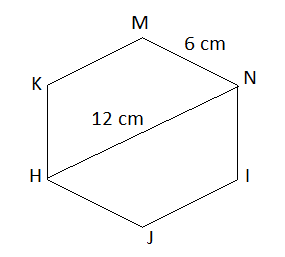
Vì lục giác MNIJHK đều nên sáu cạnh bằng nhau và ba đường chéo chính bằng nhau, nên:
HK = MN = 6 cm
IK = NH = 12 cm.
Vậy HK = 6cm, IK = 12cm.
Bài 9 trang 67 sách bài tập Toán lớp 6 Tập 1: Cho lục giác đều ABCDEG.
a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần
b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
Lời giải:
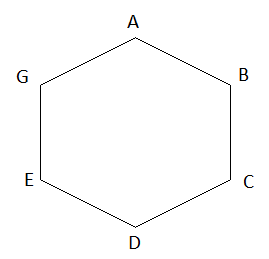
a) Từ đỉnh A có 3 đường chéo là AC, AD, AE
Từ đỉnh B có 3 đường chéo là BD, BE, BG
Từ đỉnh C có 3 đường chéo là CE, CG, CA
Từ đỉnh D có 3 đường chéo là DB, DA, DG
Từ đỉnh E có 3 đường chéo là EC, EB, EA
Từ đỉnh G có 3 đường chéo là GB, GC, GD
Có 9 đường chéo được đếm 2 lần
b) Lục giác đó có số đường chéo là 18 : 2 = 9
Lý thuyết Hình vuông, Tam giác đều, Lục giác đều
1. Hình vuông
Hình vuông có:
+ Bốn đỉnh.
+ Bốn cạnh bằng nhau.
+ Bốn góc bằng nhau và bằng góc vuông.
+ Hai đường chéo của hình vuông bằng nhau.
Ví dụ:
Hình vuông ABCD có:
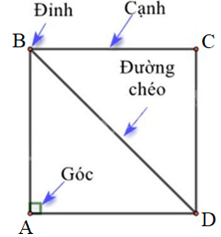
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: AB = BC = CD = DA.
- Bốn góc ở các đỉnh A, B, C, D là góc vuông.
- Hai đường chéo bằng nhau: AC = BD.
Cách vẽ hình vuông
Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng a (cm).
Bước 1: Vẽ đoạn thẳng AB = a (cm).
Bước 2: Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = a (cm).
Bước 3: Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = a (cm).
Bước 4: Nối C với D ta được hình vuông ABCD.
2. Tam giác đều
Tam giác đều có:
+ Ba đỉnh.
+ Ba cạnh bằng nhau.
+ Ba góc ở ba đỉnh bằng nhau.
Ví dụ:
Tam giác đều ABC có:
- Ba đỉnh A, B, C.
- Ba cạnh bằng nhau: AB = BC = CA.
- Ba góc đỉnh A, B, C bằng nhau.
Cách vẽ tam giác đều
Cách vẽ tam giác đều cạnh a (cm) bằng thước và compa:
Bước 1: Dùng thước vẽ đoạn thẳng AB = a (cm).
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.
Bước 3: Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4: Dùng thước vẽ các đoạn thẳng AC và BC.
Ta được tam giác ABC đều cạnh a (như hình vẽ).
3. Lục giác đều
Hình lục giác đều có sáu đỉnh, sáu cạnh bằng nhau, sáu góc ở các đỉnh bằng nhau, ba đường chéo chính bằng nhau.
Ví dụ:
Lục giác đều ABCDEF có:
- Sáu đỉnh A, B, C, D, E, F.
- Sáu cạnh bằng nhau: AB = BC = CD = DE = EF.
- Sáu góc đỉnh A, B, C, D, E, F bằng nhau.
- Ba đường chéo chính bằng nhau AD = BE = CF.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
