Với giải Bài 3.32 trang 72 Toán 8 Tập 1 Kết nối tri thức chi tiết trong Bài 14: Hình thoi và hình vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 14: Hình thoi và hình vuông
Bài 3.32 trang 72 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
Lời giải:
Giả sử có hình thoi ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.
Ta cần chứng minh EFGH là hình chữ nhật. Thật vậy:
Do ABCD là hình thoi nên AB = BC = CD = DA.
Do E, H lần lượt là trung điểm của AB, AD nên AH = DH = AE = BE.
Tam giác AHE có AH = AE nên là tam giác cân tại A, suy ra .
Mà
Suy ra .
Tương tự, ta có tam giác DHG cân tại D nên
Mặt khác, do ABCD là hình thoi nên AB // CD, suy ra
Khi đó
Mà
Suy ra
Chứng minh tương tự như trên ta cũng có .
Tứ giác EFGH có bốn góc vuông nên là hình chữ nhật.
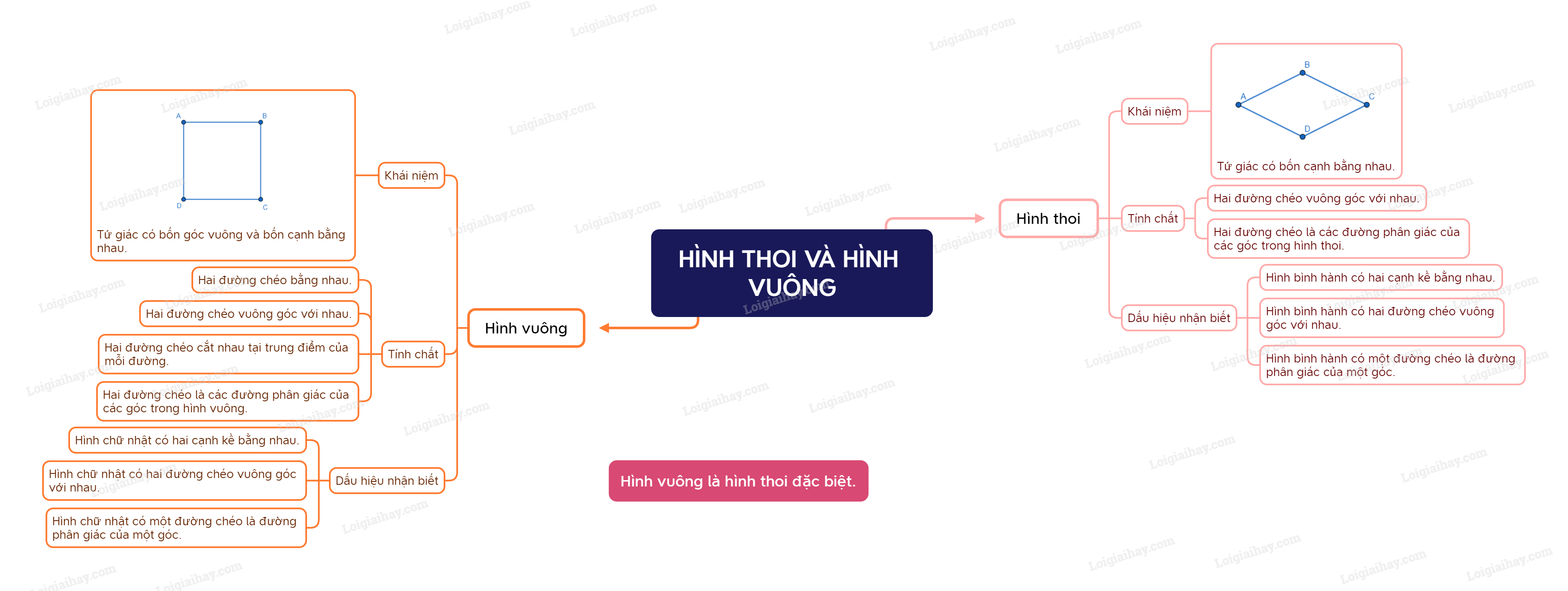
Sơ đồ tư duy Hình thoi và hình vuông.
Video bài giảng Toán 8 Bài 14: Hình thoi và hình vuông - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 68 Toán 8 Tập 1: Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48)....
Câu hỏi trang 68 Toán 8 Tập 1: Hãy viết giả thiết, kết luận của câu c trong Định lí 2....
Luyện tập 1 trang 69 Toán 8 Tập 1: Trong Hình 3.51, hình nào là hình thoi? Vì sao?....
Câu hỏi trang 70 Toán 8 Tập 1: Hãy viết giả thiết, kết luận của câu a trong Định lí 4....
Vận dụng trang 71 Toán 8 Tập 1: Trở lại tình huống mở đầu....
Bài 3.29 trang 71 Toán 8 Tập 1: Tìm hình thoi và hình vuông trong Hình 3.55.....
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
