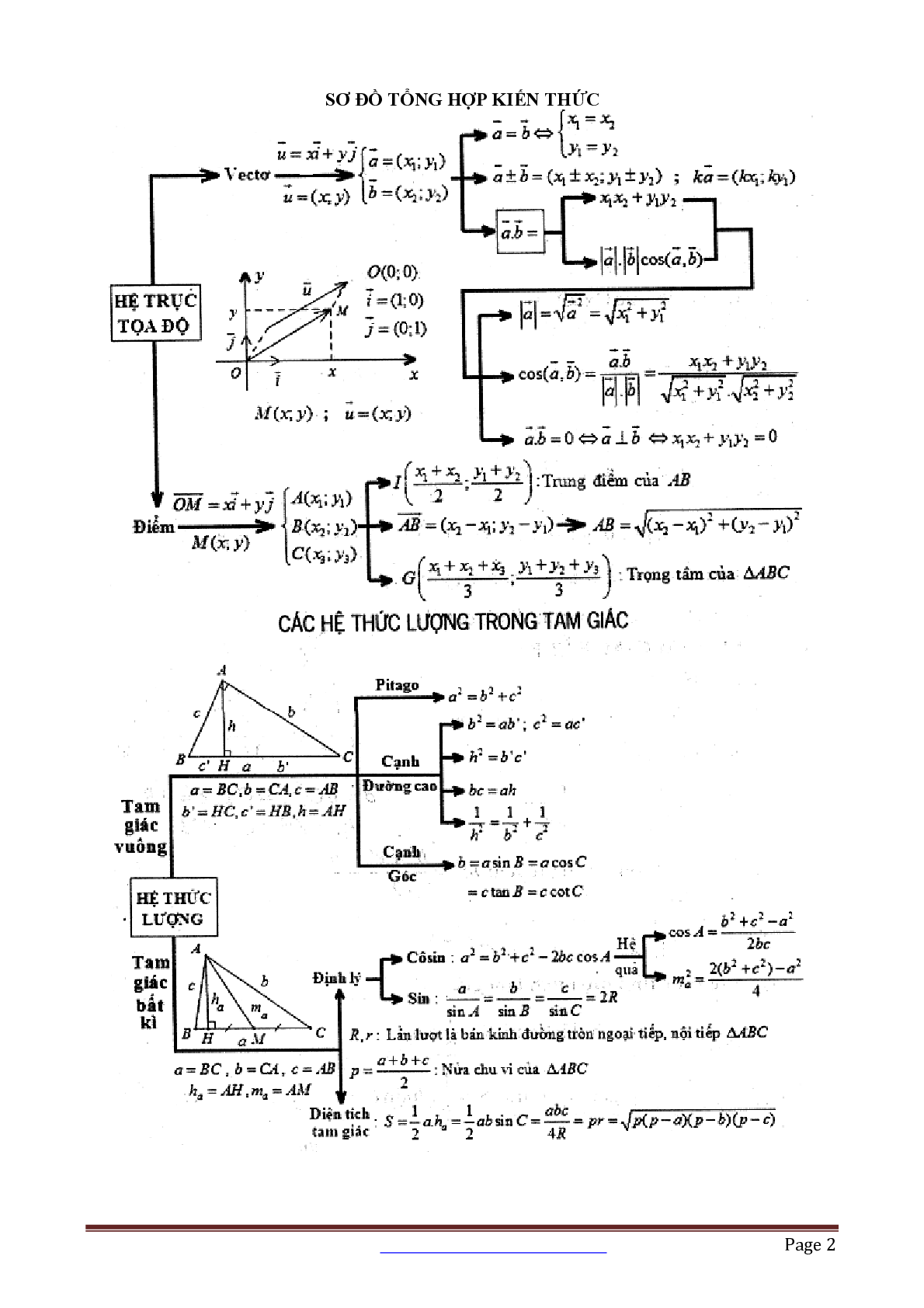
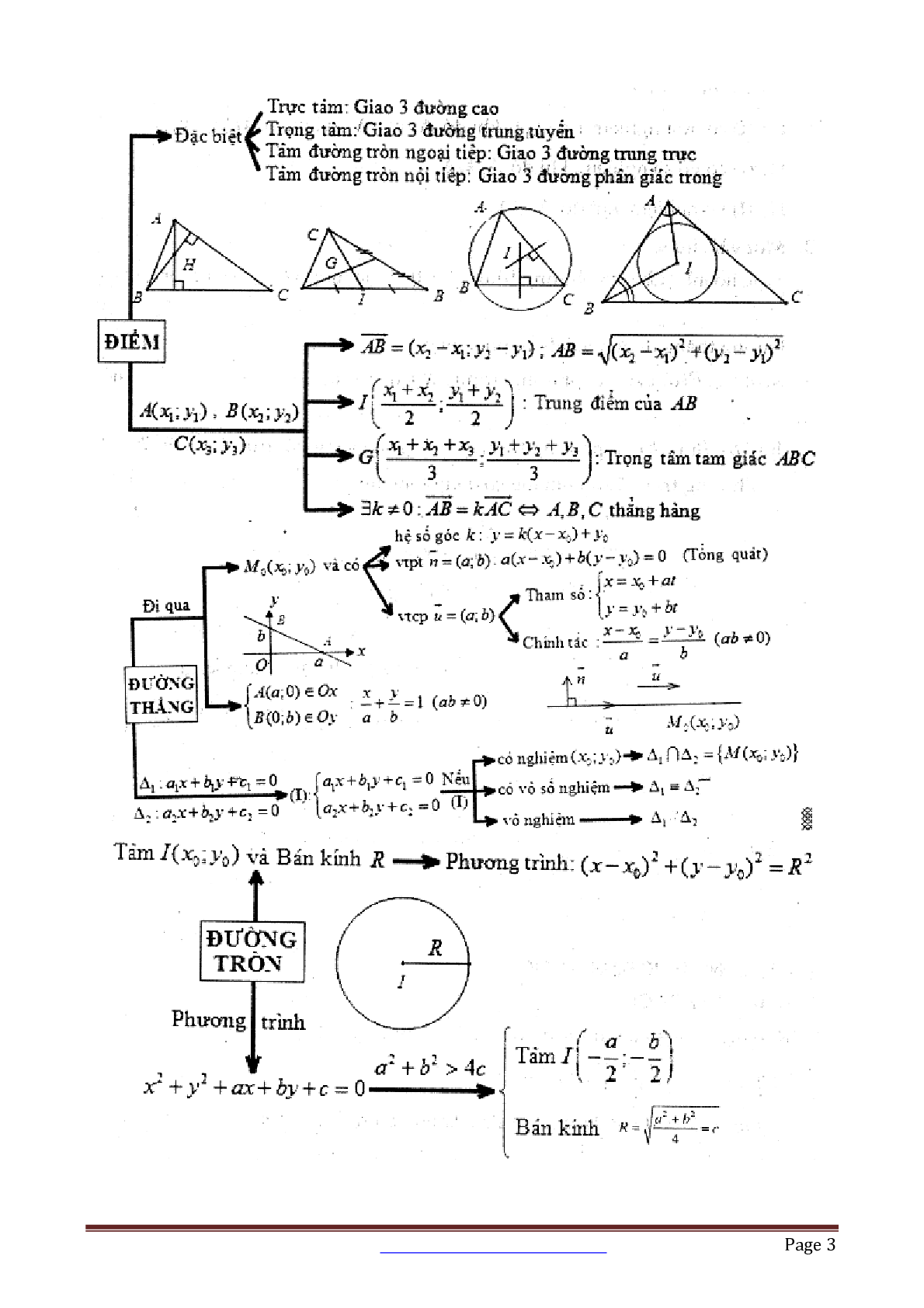
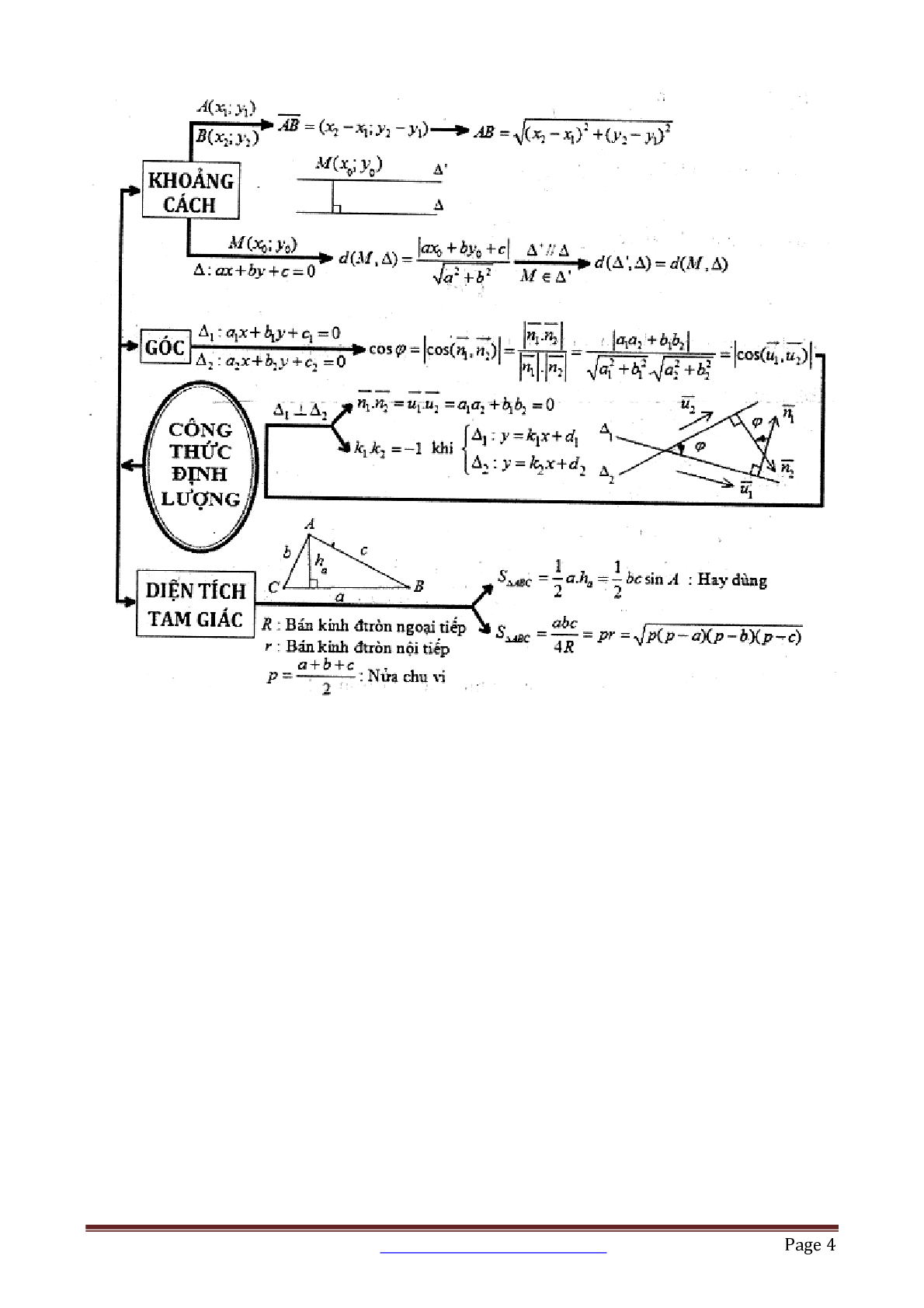
Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 17 dạng toán hình học giải tích phẳng Oxy, tài liệu bao gồm 152 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Phần 1: Tổng hợp kiến thức cơ bản

Phần 2: Những bài toán cơ bản

Phần 3: Bài toán hình học Oxy

Phần 4: Sáng tạo và sự phát triển từ các bài toán hình học phải thuần túy

Phần 5: Bài tập tổng hợp

17 dạng toán hình học giải tích phẳng Oxy

Phương pháp tọa độ trong mặt phẳng

§1. Phương trình tổng quát của đường thẩng

A. Tóm tắt giáo khoa

I. Phương trình tổng quát củ̉a đường thẳng

1. Vectơ pháp tuyến của đường thẳng

* Địhh nghĩa: Vectơ \(\vec n \ne \vec 0\) là vectơ pháp tuyến của đường thẳng \(\Delta \) \( \Leftrightarrow \) giá của \(\overrightarrow {\rm{n}}  \bot \Delta \)

* Nhận xét: \(\vec n\) là vectơ pháp tuyến của \(\Delta ;{\rm{k}} \ne 0 \Rightarrow {\rm{k}}\vec n\) là vectơ pháp tuyến của \(\Delta \).

2. Phương trình tổng quát của đường thẳng

Trong mặt phẳng tọa độ, phương trình tổng quát của đường thẳng \(\Delta \) có dạng:

\({\rm{ax}} + {\rm{by}} + {\rm{c}} = 0{\rm{ va }}{{\rm{a}}^2} + {{\rm{b}}^2} \ne 0\)

Lúc đó, đường thẩng \(\Delta \) có vectơ pháp tuyến là: \(\overrightarrow {\rm{n}}  = ({\rm{a}};{\rm{b}})\).

3. Các dạng đặc biệt của phương trình tổng quát

a) Dạng 1: Dường thẳng \(\Delta \) đi qua I( \(\left. {{x_0};{y_0}} \right)\), có vectơ pháp tuyến \(\vec n = (a;b)\)

Phương trình của \(\Delta \) là:

\(\Delta :{\rm{a}}\left( {{\rm{x}} - {{\rm{x}}_0}} \right) + {\rm{b}}\left( {{\rm{y}} - {{\rm{y}}_0}} \right) = 0\)

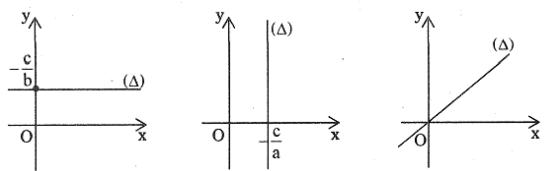
b) Dạng 2: Cho đường thẳng \(\Delta \): ax + by + c = 0 \[\left( {{a^2} + {b^2} \ne 0} \right)\]

* a = 0: Đường thẳng \(\Delta :\) by \( + {\rm{c}} = 0\) vuông góc với trục \({\rm{Oy}}\) tại điểm \(\left( {0; - \frac{{\rm{c}}}{{\rm{b}}}} \right)\)

* \({\rm{b}} = 0\) : Đường thẳng \(\Delta :{\rm{ax}} + {\rm{c}} = 0\)

vuông góc với trục \({\rm{Ox}}\) tại điểm \(\left( { - \frac{{\rm{c}}}{{\rm{a}}};0} \right)\)

* \({\rm{c}} = 0\) : Đường thẳng \(\Delta :{\rm{ax}} + {\rm{by}} = 0\) đi qua gốc tọa độ,

c) Dạng 3: Phương trình đường thẳng theo đoạn chắn:

Đường thẳng \(\Delta \) cắt Ox Oy lần lượt tại \({\rm{A}}({\rm{a}};0),{\rm{B}}(0;{\rm{b}})\) với a.b \( \ne 0\).

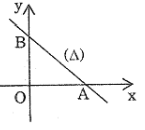
Phương trình của \(\Delta \) là:

\(\frac{x}{a} + \frac{y}{b} = 1\)

d) Dạng 4: Phương trình của đường thẳng theo hệ số góc:

* Cho đường thẳng \(\Delta \): ax + by  + c =0 (1) .

Nếu \(b \ne 0\) thì

\((1) \Leftrightarrow \left( {{\rm{y}} = {\rm{kx}} + {\rm{m}}\quad \left( {} \right.} \right.\) với \(\left. {{\rm{k}} =  - \frac{{\rm{a}}}{{\rm{b}}};{\rm{m}} =  - \frac{{\rm{c}}}{{\rm{b}}}} \right)\)

Ta gọi \(k =  - \frac{a}{b}\) là hệ số góc của đường thẳng \(\Delta \) (không cùng phương với O ).

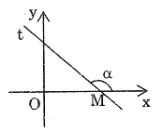
* Ý nghĩa hình học của hệ số góc:

Xét đường thẳng \(\Delta :{\rm{y}} = {\rm{kx}} + {\rm{m}}\)

- Nếu \(k \ne 0\) thì \(k = {\mathop{\rm tg}\nolimits} \alpha \)

Với \(\alpha \) là góc hợp bởi tia Mx và tia Mt (tia của \(\Delta \) nằm phía trên Ox ).

- Nếu \({\rm{k}} = 0\) thì \(\Delta :{\rm{y}} = {\rm{m}}\) là đường thẳng cùng phương với trục Ox.

II. Vị trí tương đối của hai đường thẳng

Cho hai đường thẳng: \({\Delta _1}:{{\rm{a}}_1}{\rm{x}} + {{\rm{b}}_1}{\rm{y}} + {{\rm{c}}_1} = 0;\quad {\Delta _2}:{{\rm{a}}_2}{\rm{x}} + {{\rm{b}}_2}{\rm{y}} + {{\rm{c}}_2} = 0\)

Đặt

\(D = \left| {\begin{array}{*{20}{l}}{{a_1}}&{{b_1}}\\{{a_2}}&{{b_2}}\end{array}} \right| = {a_1}{b_2} - {a_2}{b_1}\)

\(\begin{array}{l}{D_x} = \left| {\begin{array}{*{20}{l}}{{b_1}}&{{c_1}}\\{{b_2}}&{{c_2}}\end{array}} \right| = {b_1}{c_2} - {b_2}{c_1}\\{D_y} = \left| {\begin{array}{*{20}{l}}{{c_1}}&{{a_1}}\\{{c_2}}&{{a_2}}\end{array}} \right| = {c_1}{a_2} - {c_2}{a_1}\end{array}\)

\(1)\) cắt \({\Delta _2} \Leftrightarrow {\rm{D}} \ne 0\). Lúc đó \({\Delta _1}\) cắt \({\Delta _2}\) tại điểm \({\rm{M}}\left( {\frac{{{{\rm{D}}_{\rm{x}}}}}{{\rm{D}}};\frac{{{{\rm{D}}_{\rm{y}}}}}{{\rm{D}}}} \right)\)

2) \({\Delta _1}//{\Delta _2} \Leftrightarrow D = 0\) và \(\left( {{D_x} \ne 0} \right.\) hay \(\left. {{D_y} \ne 0} \right)\)

3) \({\Delta _1} \equiv {\Delta _2}\quad  \Leftrightarrow {\rm{D}} = {{\rm{D}}_{\rm{x}}} = {{\rm{D}}_{\rm{y}}} = 0\)

4) \({\Delta _1} \bot {\Delta _2} \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} = 0\)

* Đặc biệt :

Nếu \({{\rm{a}}_2} \cdot {{\rm{b}}_2} \cdot {{\rm{c}}_2} \ne 0\) thì:

1) \({\Delta _1}\) căt \({\Delta _2} \Leftrightarrow \frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}\)

2) \({\Delta _1}//{\Delta _2} \Leftrightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}\)

3) \({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}\)

* Chú ý: Cho hai đường thẳng: \({\Delta _1}:{\rm{y}} = {{\rm{k}}_1}{\rm{x}} + {{\rm{m}}_1};\quad {\Delta _2}:{\rm{y}} = {{\rm{k}}_2}{\rm{x}} + {{\rm{m}}_2}\)

1) \({\Delta _1}\) cắt \({\Delta _2} \Leftrightarrow {{\bf{k}}_1} \ne {{\bf{k}}_2}\)

2) \({\Delta _1}//{\Delta _2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{k_1} = {k_2}}\\{{m_1} \ne {m_2}}\end{array}} \right.\)

3) \({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{k_1} = {k_2}}\\{{m_1} = {m_2}}\end{array}} \right.\)

4) \({\Delta _1} \bot {\Delta _2} \Leftrightarrow {{\rm{k}}_1},{{\rm{k}}_2} =  - 1\)

B. Các dạng toán

* Vấn dề 1: viết phương trình tổng quát của đường thẩng

1. Phương pháp

Viết phương trình tổng quát của đường thẳng \(\Delta \).

a) Dạng 1:   qua \(I\left( {{x_0};{y_0}} \right)\), có vectơ pháp tuyến \(\vec n = (a;b)\)

* Dùng công thức \(\Delta :a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)

* Biến đổi về dạng \({\rm{ax}} + {\rm{by}} + {\rm{c}} = 0\).

b) Dạng 2: \(\Delta \) qua \(I\left( {{x_0};{y_0}} \right)\), cùng phương với vectơ \(\vec u = (a;b)\)

* Vectơ pháp tuyến của \(\Delta \) là: \(\vec n = (b; - a)\) hay \(\vec n = ( - b;a)\)

* Đưa về dạng 1 .

c) Dạng 3: \(\Delta \) qua \(I\left( {{x_0},{y_0}} \right)\), cùng phương đường thẳng \(D:ax + by + c = 0\)

* Vectơ pháp tuyến của \(\Delta \) là: \({\vec n_\Delta } = {\vec n_D} = (a;b)\)

* Đưa về dạng 1 .

d) Dạng 4: A qua I \(\left( {{x_0},{y_0}} \right)\), vuông góc đường thẳng \(D:ax + by + c = 0\)

* Vectơ pháp tuyến của \(\Delta \) là: \({\overrightarrow {\rm{n}} _\Delta } = ({\rm{b}}; - {\rm{a}})\) hay \({\overrightarrow {\rm{n}} _\Delta } = ( - {\rm{b}};{\rm{a}})\)

* Đưa về dạng 1 .

e) Dạng 5: \(\Delta \) qua \(I\left( {{x_0};{y_0}} \right)\), có hệ số góc k :

* Đặt \({\rm{k}} = \frac{{\rm{n}}}{{\rm{m}}}\) thì vectơ pháp tuyến của \(\Delta \) là \({\overrightarrow {\rm{n}} _\Delta } = ({\rm{n}}; - {\rm{m}})\) hay \({\overrightarrow {\rm{n}} _\Delta } = ( - {\rm{n}};{\rm{m}})\)

* Đưa về dạng 1 .

f) Dạng 6:  qua gai điểm A (a;0), B ( 0;b) với ab khác 0

* Dùng công thức: \(\Delta :\frac{x}{a} + \frac{y}{b} = 1\)

* Biến đổi về dạng phương trình tổng quát

g) Dạng 7: \(\Delta \) qua hai điểm phân biệt \(A\left( {{x_A},{x_B}} \right),B\left( {{x_B},{y_B}} \right)\)

* Tính tọa độ của \(\overrightarrow {{\rm{AB}}} \)

* Đưa về dạng 2 .

2. Ví dụ:

Vi dụ 1: Viết phương trình tổng quát của đường thẳng \(\Delta \) :

a) Qua \({\rm{I}}(3; - 4)\), có vectơ pháp tuyến \(\overrightarrow {\rm{n}}  = (2; - 1)\)

b) Qua \({\rm{I}}( - 3;2)\), cùng phương với vectơ \(\overrightarrow {\rm{u}}  = (1;2)\)

c) Qua \({\rm{I}}(1;3)\) và cùng phương với đường thẳng \({\rm{D}}:2{\rm{x}} + {\rm{y}} + 1 = 0\)

d) Qua \({\rm{I}}(2;1)\) và vuông góc đường thẳng \({\rm{D}}:2{\rm{x}} - {\rm{y}} - 9 = 0\)

e) Qua \({\rm{I}}( - 3;5)\) và có hệ số góc \({\rm{k}} =  - 3\)

f) Qua hai điểm \({\rm{A}}( - 2;0)\) và \({\rm{B}}(0;3)\)

g) Qua hai điểm \({\rm{A}}(6;1)\) và \({\rm{B}}( - 2;3)\).

Vấn đề 2: Vị trí tương đối của hai đường thẳng

1. Phương pháp

Xét vị trí tương đối của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\).

* Dạng 1: Dùng phương trình tổng quát:

\({\Delta _1}:{{\rm{a}}_1}{\rm{x}} + {{\rm{b}}_1}{\rm{y}} + {{\rm{c}}_1} = 0\)

\({\Delta _2}:{{\rm{a}}_2}{\rm{x}} + {{\rm{b}}_2}{\rm{y}} + {{\rm{c}}_2} = 0\)

Xem mục II phần tóm tắt giáo khoa.

* Dạng 2: Dùng hệ số góc

\({\Delta _1}:{\rm{y}} = {{\rm{k}}_1}{\rm{x}} + {{\rm{m}}_1}\) \({\Delta _2}:{\rm{y}} = {{\rm{k}}_2}{\rm{x}} + {{\rm{m}}_2}\)

Xem trường hợp đặc biệt ở mục II phần tóm tắt giáo khoa.

2. Ví dụ

Ví dụ 2: Xét vị trí tương đối của các cặp đường thẳng sau và tìm giao điểm của chúng (nếu có).

a) \({\Delta _1}:2x + 3y + 1 = 0\) và \({\Delta _2}:4x + 5y - 6 = 0\)

b) \({\Delta _1}:4{\rm{x}} - {\rm{y}} + 2 = 0\) và \({\Delta _2}: - 8{\rm{x}} + 2{\rm{y}} + 1 = 0\)

c) \({\Delta _1}:4x + 5y - 6 = 0\) và \({\Delta _2}:8x + 10y - 12 = 0\)

Ví dụ 3: Xét vị trí tương đối của các cặp đường thẳng sau và tìm giao điểm của chúng (nếu có).

a) \({\Delta _1}:y =  - 3x + 2\) và \({\Delta _2}:y = 4x - 3\)

b) \({\Delta _1}:y = 2x - 5\) và \({\Delta _2};y = 2x + 3\)

c) \({\Delta _1}:y = 4{\rm{x}} - 3\) và \({\Delta _2}:y =  - \frac{1}{4}{\rm{x}} + 1\)

C. Bài tập luyện tập

1.1. Cho tam giác ABC với \({\rm{A}}(2;3),{\rm{B}}( - 2;5),{\rm{C}}(4;3)\).

a) Viết phương trình tổng quát của các đường thẳng đi qua các cạnh của tam giác ABC.

b) Viết phương trình các đường thẳng đi qua các đường cao của tam giác ABC

c) Tìm tọa độ trực tâm của tam giac ABC

d) Viết phương trình đường thẳng đu qua trung tuyến AM của tam giác ABC

1.2. Cho tam giác \({\rm{ABC}}\) với \({\rm{A}}(3; - 5),{\rm{B}}(1; - 3),{\rm{C}}(2; - 2)\)

b) Vẽ hình bình hành ABCD. Viết phương trình các đường thẳng đi qua các cạnh của nó.

1.3. Viết phương trình đường thẳng đi qua các cạnh và các đường trung trực của  biết trung điểm của các cạnh BC, CA, BC lần lượt là:

\({\rm{M}}( - 1; - 1),{\rm{N}}(1;9),{\rm{P}}(9;1)\)

1.4. Cho tam giác ABC có \({\rm{A}}( - 4; - 5)\) và hai đường cao:

\[\begin{array}{*{20}{c}}{{\rm{B}}{{\rm{B}}^\prime }:5{\rm{x}} + 3{\rm{y}} - 4 = 0}\\{{\rm{C}}{{\rm{C}}^\prime }:3{\rm{x}} + 8{\rm{y}} + 13 = 0}\end{array}\]

Viết phương trình các đường thẳng đi qua các cạnh của  và đường cao thứ ba.

1.5. Cho điểm \({\rm{M}}(1;2)\). Viết phương trình đường thẳng \(\Delta \) qua M và chắn trên hai trục tọa độ hai đoạn thẳng có độ dài bằng nhau.

1.6. Viết phương trình đường thẳng \(\Delta \) :

a) Qua \({\rm{M}}( - 2; - 4)\) và cắt Ox, Oy lần lượt tại A và B sao cho \(\Delta {\rm{OAB}}\) là tam giác vuông cân.

b) Qua \({\rm{N}}(5; - 3)\) và cắt Ox, Oy lần lượt tại A và B sao cho N là trung điểm của AB.

1.7. Viết phương trình tổng quát của:

a) Đường thẳng Ox.

b) Đường thẳng Oy.

c) Đường thẳng đi qua \({\rm{M}}\left( {{{\rm{x}}_0};{{\rm{y}}_0}} \right)\) và song song với \({\rm{Ox}}\quad \left( {{{\rm{y}}_0} \ne 0} \right)\).

d) Đường thẳng đi qua \({\rm{M}}\left( {{{\rm{x}}_0};{{\rm{y}}_0}} \right)\) và vuông góc với Ox.

e) Đường thẳng \({\rm{OM}}\) với \({\rm{M}}\left( {{{\rm{x}}_0};{{\rm{y}}_0}} \right)\) khác gốc tọa độ O.

1.8. Viết phương trình đường thẳng đi qua điểm \({\rm{M}}(2;5)\) và cách đều hai điểm \({\rm{P}}( - 1;2)\) và \({\rm{Q}}(5;4)\).

1.9. Cho hai đường thẳng: \({\Delta _1}:({\rm{m}} + 3){\rm{x}} - 2{\rm{y}} + 6 = 0\); \({\Delta _2}:{\rm{mx}} + {\rm{y}} + 2 - {\rm{m}} = 0\)

Định m để:

a)  cắt \({\Delta _2}\)

b) \({\Delta _1}//{\Delta _2}\)

c) \({\Delta _1} \equiv {\Delta _2}\)

d) \({\Delta _1} \bot {\Delta _2}\)

1.10. Định b để ba đường thẳng sau đồng qui:

\({\Delta _1}:4{\rm{x}} + 3{\rm{y}} + {\rm{m}} = 0;\quad {\Delta _2}:3{\rm{x}} + {\rm{y}} = 0;\quad {\Delta _3}:9{\rm{x}} + 2{\rm{y}} + 6 = 0\)

§ 2. Phương trình tham số của đường thẳng

A. Tóm tắt giáo khoa

I. Vectơ chỉ phương của đường thẳng

* Định nghĩa: Vectơ \[{\rm{\vec u}} \ne \vec 0\]là vectơ chĩ phương của đường thẳng  \( \Leftrightarrow \) giá của \[{\rm{\vec u}}\] cùng phương \(\Delta \).

* Nhận xét: \(\overrightarrow {\rm{u}} \) là vectơ chỉ phương của \(\Delta ;{\rm{k}} \ne 0 \Rightarrow {\rm{k}}\vec u\) là vectơ chỉ phương của \(\Delta \).

* Chú y:

a) Đường thẳng \(\Delta :ax + by + c = 0\) có

- Vectơ pháp tuyến là: \(\vec n = (a;b)\)

- Vectơ chỉ phương là: \(\overrightarrow {\rm{u}}  = ({\rm{b}}; - {\rm{a}})\) hay \(\overrightarrow {\rm{u}}  = ( - {\rm{b}};{\rm{a}})\)

- Hệ số góc là \(k =  - \frac{a}{b}(b \ne 0)\)

b) Nếu \(\overrightarrow {\rm{u}}  = ({\rm{a}};{\rm{b}})\) là vectơ chỉ phương của \(\Delta \), thì vectơ pháp tuyến là: \(\overrightarrow {\rm{n}}  = ({\rm{b}}; - {\rm{a}})\) hay \(\overrightarrow {\rm{n}}  = ( - {\rm{b}};{\rm{a}})\); hệ số góc của \(\Delta \) là \({\rm{k}} = \frac{{\rm{b}}}{{\rm{a}}}({\rm{a}} \ne 0)\).