Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển chọn bài tập trắc nghiệm thể tích khối chóp, tài liệu bao gồm 68 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Thể tích khối chóp

Dạng 1. Khối chóp có các cạnh bên vuông góc với đáy

Dạng 2. Khối chíp có hình chiếu của đỉnh lên mặt phẳng đáy

Dạng 3. Khối chóp có mặt bên vuông góc với đáy

Dạng 4. Khối chóp đều

Dạng 5. Tỉ lệ thể tích

Tuyển chọn bài tập trắc nghiệm thể tích khối chóp

Chuyên đề 2. Thể tích khối chóp

Công thức chung: ${\rm{V}} = \frac{1}{3}{\rm{Bh}}$

Trong đó: ${\rm{B}}$ là diện tích đáy, h là chiều cap

Dạng 1. Khối chóp có cạnh bên vuông góc đáy

Một số chú ý khi giải toán

- Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên đó chính là đường cao.

- Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì cạnh bên là giao tuyến của hai mặt đó vuông góc với đáy.

Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. SA vuông góc với mặt phẳng (ABC). Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng ${30}^{°}$. Tính theo a thể tích khối chóp S.ABC.

A. $V = \frac{{{a^3}\sqrt {13} }}{2}$

B. $V = \frac{{{a^3}}}{{12}}$

C. ${\rm{V}} = \frac{{3{{\rm{a}}^3}\sqrt {13} }}{2}$

D. ${\rm{V}} = \frac{{5{{\rm{a}}^3}\sqrt {13} }}{2}$

Hướng dẫn giải

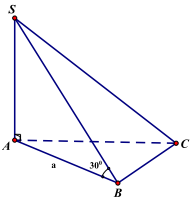
Ta có góc giữa đường thẳng SB và mặt phẳng (ABC) là $\text{SBA}={30}^{°}$.

${S_{ABC}} = \frac{1}{2} \cdot \frac{{a\sqrt 3 }}{2} \cdot a = \frac{{{a^2}\sqrt 3 }}{4};$

$SA = \tan SBA \cdot AB = \frac{{a\sqrt 3 }}{3}$

${{\rm{V}}_{{\rm{S}}.{\rm{ABC}}}} = \frac{1}{3}\;{{\rm{S}}_{{\rm{ABC}}}} \cdot {\rm{SA}} = \frac{{{{\rm{a}}^3}}}{{12}}.$

Vậy chọn đáp án A.

Câu 2. Cho hình chóp S.ABCD có chiều cao SA bằng a. Mặt đáy ABCD là hình thoi cạnh a, góc ABC bằng ${60}^{°}$. Tính thể tích khối chóp S.ABCD theo a.

A. $\frac{{\sqrt {21} }}{{15}}a$

B. $\frac{{\sqrt {23} }}{{14}}a$

C. $\frac{{\sqrt {21} }}{{14}}{\rm{a}}$

D. $\frac{{\sqrt {21} }}{4}{\rm{a}}$

Hướng dẫn giải

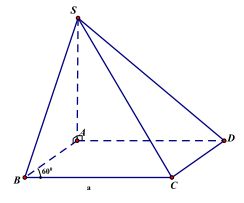
Tam giác ABC đều cạnh a nên

${S_{ABC}} = {a^2}\frac{{\sqrt 3 }}{4}$ $\Rightarrow$ Diện tích đáy: ${S_{ABCD}} = 2 \cdot {S_{ABC}} = {a^2}\frac{{\sqrt 3 }}{2}$

Thể tích khối chóp:

${\rm{V}} = {{\rm{a}}^2}\frac{{\sqrt 3 }}{2} \cdot {\rm{a}} = \frac{{{{\rm{a}}^3}\sqrt 3 }}{2}$

Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông với ${\rm{AC}} = \frac{{{\rm{a}}\sqrt 2 }}{2}$.

Cạnh bên SA vuông góc với mặt phẳng (ABCD), cạnh bên SB hợp với mặt phẳng (ABCD) một góc ${60}^{°}$. Tính thể tích khối chóp S.ABCD.

A. $\frac{{{a^3}\sqrt 3 }}{{24}}$

B. $\frac{{3{a^3}\sqrt 3 }}{{24}}$

C. $\frac{{{a^3}\sqrt 3 }}{8}$

D. $\frac{{3{a^3}\sqrt 3 }}{8}$

Hướng dẫn giải

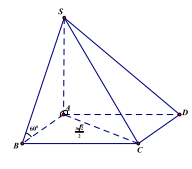
Ta có: AB là hình chiếu của SB lên mặt phẳng (ABCD) nên

$(\text{SB},(\text{ABCD}\left)\right)=\text{SBA}={60}^{°}\text{; }$

${\rm{SA}} \bot ({\rm{ABCD}}) \Rightarrow {\rm{SA}}$ khối chóp ${\rm{S}}.{\rm{ABCD}}$

Tính được ${\rm{AB}} = \frac{a}{2};{\rm{SA}} = \frac{{a\sqrt 3 }}{2};{{\rm{S}}_{{\rm{ABCD}}}} = \frac{{{a^2}}}{4}$

${{\rm{V}}_{{\rm{S}}.{\rm{ABCD}}}} = \frac{1}{3}.S\;{\rm{A}} \cdot {{\rm{S}}_{{\rm{ABCD}}}} = \frac{{{{\rm{a}}^3}\sqrt 3 }}{{24}}({\rm{dvtt}})$

Vậy chọn đáp án ${\rm{A}}$.

Câu 4. Cho tứ diện OABC có đáy OBC là tam giác vuông tại $O,OB = a,OC =$ ${\rm{a}}\sqrt 3 ,(a > 0)$ và đường cao $OA = {\rm{a}}\sqrt 3$. Tính thể tích khối tứ diện theo a.

A. $V = \frac{{{a^3}}}{2}$

B. ${\rm{V}} = \frac{{{{\rm{a}}^3}}}{3}$

C. $V = \frac{{{a^3}}}{6}$

D. ${\rm{V}} = \frac{{{{\rm{a}}^3}}}{{12}}$

Hướng dẫn giải

Ta có:

${S_{OBC}} = \frac{1}{2}OB.OC = \frac{1}{2}a(a\sqrt 3 ) = \frac{{{a^2}\sqrt 3 }}{2}$

Thế tích khối tứ diện

${\rm{V}} = \frac{1}{3}\;{{\rm{S}}_{{\rm{OBC}}}} \cdot {\rm{OA}} = \frac{1}{3}\left( {\frac{{{{\rm{a}}^2}\sqrt 3 }}{2}} \right)({\rm{a}}\sqrt 3 ) = \frac{{{{\rm{a}}^3}}}{2}$.

 Vậy chọn đáp án A.

Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh $a,ABC = {60^0}$ cạnh SA vuông góc với đáy và SC tạo với đáy một góc ${60}^{°}$. Tính theo a thể tích khối chóp SABCD.

A. $V = \frac{{{a^3}}}{2}$

B. $V = \frac{{{a^3}}}{3}$

C. $V = \frac{{2{a^3}}}{3}$

D. $V = \frac{{{a^3}}}{9}$

Hướng dẫn giải

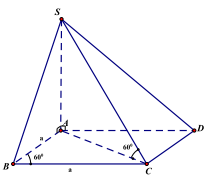
Ta có  đều nên AC=a.

Có:

$BD = \sqrt {A{B^2} + A{D^2} - 2AB \cdot AD \cdot \cos 120}$ $\Rightarrow BD = a\sqrt 3$

Suy ra ${S_{ABCD}} = \frac{1}{2}AC \cdot BD = \frac{{{a^2}\sqrt 3 }}{2}$

Mặt khác $\text{SA}=\text{AC}\cdot \tan {60}^{°}=\text{a}\sqrt{3}\text{.}$

Vậy ${{\rm{V}}_{{\rm{S}}.{\rm{ABCD}}}} = \frac{1}{3}{\rm{SA}} \cdot {{\rm{S}}_{{\rm{ABCD}}}} = \frac{{{{\rm{a}}^3}}}{2}$.

Vậy ta chọn đáp án A.

Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thoi có cạnh bằng $\text{BAD}={120}^{°}$ và cạnh bên SA vuông góc với đáy. Biết mặt phẳng (SBC) và đáy bằng ${60}^{°}$. Tính theo a thể tích khối chóp S.ABCD.

A. $V = \frac{{{a^3}\sqrt 3 }}{4}$

B. $V = \frac{{3 \cdot {a^3}\sqrt 3 }}{4}$

C. $V = \frac{{3 \cdot {a^3}}}{4}$

D. $V = \frac{{3 \cdot {a^3}\sqrt 3 }}{5}$

Hướng dẫn giải

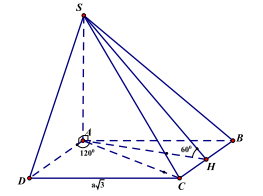
Do đáy ABCD là hình thoi có

$\text{BAD}={120}^{°}$nên các tam giác ABC, ADC đều cạnh a $\sqrt 3$.

Gọi H là trung điểm của BC, ta có:

$\begin{array}{l}AH\perp BC,SA\perp BC\Rightarrow BC\perp SH\\ \text{Do do: }\left(\right(\text{SBC});(\text{ABCD}\left)\right)=(\text{AH};\text{SH})=\text{SHA}={60}^{°}\end{array}$

Tam giác SAH vuông tại A: $\text{SA}=\text{AH}\cdot \tan {60}^{°}=\frac{3\text{a}}{2}$

Ta có: ${S_{ABCD}} = 2{S_{ABC}} = 2\frac{{{{(a\sqrt 3 )}^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{2}$.

Suy ra: ${V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{{3{a^3}\sqrt 3 }}{4}$. Vậy chọn đáp án B.

Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, $\text{AB}=2\text{a},\text{BAC}={60}^{°}$. Cạnh bên SA vuông góc với mặt phẳng (ABC) và ${\rm{SA}} = {\rm{a}}\sqrt 3$. Tính theo a thể tích khối chóp S.ABC.

A. $V = 2{a^3}$

B. $V = 3{a^3}$

C. ${\rm{V}} = {{\rm{a}}^3}$

D. $V = 4{a^3}$

Hướng dẫn giải

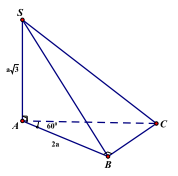
Xét tam giác ABC có:

 $$\begin{gathered} {\text{BC=AB.tan60}}^0=2a\sqrt{3}\Rightarrow S_{ABC}△ABC\cdot SA=2a^3 \\ \Rightarrow {\text{V}}_{\text{SABC}}=\frac{1}{3}{\text{S}}_{△\text{ABC}}\cdot \text{SA}=2{\text{a}}^3 \end{gathered}$$

Chọn đáp án A

Câu 8. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B có góc $\text{BAC}={30}^{°},,\text{SA}=\text{a},\text{SCA}={45}^0$ và SA vuông góc với đáy. Thể tích khối chóp S.ABC là V. Tỉ số $\frac{{\rm{V}}}{{{{\rm{a}}^3}}}$ gần giá trị nào nhất trong các giá trị sau:

A. 0,01

B. 0,05

C. 0,08

D. 1

Hướng dẫn giải

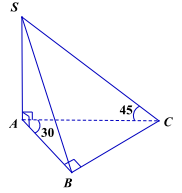
Ta có $SCA = {45^0}$

$\Rightarrow {\rm{AC}} = {\rm{SA}} \cdot \tan {\rm{SCA}} = {\rm{a}}$

$AB = AC \cdot \cos BAC = a \cdot \cos {30^0}$

 $\Rightarrow S_{△ABC}=\frac{1}{2}AB\cdot AC\sin BAC$

$= \frac{1}{2} \cdot \frac{{a \cdot \sqrt 3  \cdot a}}{2} \cdot \frac{1}{2} = \frac{{{a^2}\sqrt 3 }}{8}$

Vậy ${V_{{\rm{S}}.{\rm{ABC}}}} = \frac{1}{3} \cdot {{\rm{S}}_{{\rm{ABC}}}} \cdot {\rm{SA}} = \frac{1}{3}\frac{{{{\rm{a}}^2}\sqrt 3 }}{8} \cdot {\rm{a}} = \frac{{{{\rm{a}}^3}\sqrt 3 }}{{24}}$

$\Rightarrow \frac{{\rm{V}}}{{{{\rm{a}}^3}}} \approx 0,072 \Rightarrow$ Chọn đáp án C

Câu 9. Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có ${\rm{AB}} = 2{\rm{a}},{\rm{AD}} = {\rm{a}}$. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (SBD) bằng ${45}^{°}$. Thể tích khối chóp S.ABCD là V. Tỉ số $\frac{{\rm{V}}}{{{{\rm{a}}^3}}}$ gần nhất giá trị nào dưới đây:

A. 0,25

B. 0,5

C. 0,75

D. 1,5

Hướng dẫn giải

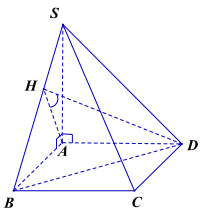
Ta có: ${S_{ABCD}} = AB \cdot AD = 2{a^2}$

$({\rm{SAB}}) \bot ({\rm{ABCD}})$ và $({\rm{SAD}}) \bot ({\rm{ABCD}})$

$({\rm{SAB}}) \cap ({\rm{SAD}}) = {\rm{SA}} \Rightarrow {\rm{SA}} \bot ({\rm{ABCD}})$

Ta có:

${\rm{AD}} \bot {\rm{AB}},{\rm{AD}} \bot {\rm{SA}} \Rightarrow {\rm{AD}} \bot ({\rm{SAB}})$

$\Rightarrow {\rm{AD}} \bot {\rm{SB}}.{\rm{K}}?{\rm{AH}} \bot {\rm{SB}} \Rightarrow {\rm{SB}} \bot ({\rm{AHD}})$

$\Rightarrow {\rm{SB}} \bot {\rm{HD}}$.

Ta có: $\left\{ {\begin{array}{*{20}{l}}{{\rm{AH}} \bot {\rm{SB}},{\rm{HD}} \bot {\rm{SB}}}\\{({\rm{SAB}}) \cap ({\rm{SBD}}) = {\rm{SB}}}\end{array}} \right.$

$\Rightarrow (({\rm{SAB}}),({\rm{SBD}})) = {\rm{AHD}} = {45^0}$

$\Rightarrow {\rm{AH}} = {\rm{AD}} = {\rm{a}}$

Xét tam giác SAB vuông tại S có:

$\begin{array}{l}\frac{1}{{{\rm{A}}{{\rm{H}}^2}}} = \frac{1}{{{\rm{S}}{{\rm{A}}^2}}} + \frac{1}{{{\rm{A}}{{\rm{B}}^2}}}\\ \Rightarrow {\rm{SA}} = \frac{{{\rm{AB}} \cdot {\rm{AH}}}}{{\sqrt {{\rm{A}}{{\rm{B}}^2} - {\rm{A}}{{\rm{H}}^2}} }} = \frac{{2{\rm{a}} \cdot {\rm{a}}}}{{\sqrt {4{{\rm{a}}^2} - {{\rm{a}}^2}} }} = \frac{{2{\rm{a}}\sqrt 3 }}{3}\end{array}$

Vậy

$\begin{array}{l}{{\rm{V}}_{{\rm{S}}.{\rm{ABCD}}}} = \frac{1}{3} \cdot {{\rm{S}}_{{\rm{ABCD}}}} \cdot {\rm{SA}} = \frac{1}{3} \cdot 2{{\rm{a}}^2} \cdot \frac{{2{\rm{a}}\sqrt 3 }}{3} = \frac{{4{{\rm{a}}^3}\sqrt 3 }}{9}\\ \Rightarrow \frac{{\rm{V}}}{{{{\rm{a}}^3}}} = \frac{{4\sqrt 3 }}{9} \approx 0,77\end{array}$

Chọn đáp án C