Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển chọn bài tập trắc nghiệm thể tích khối đa diện, tài liệu bao gồm 57 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tuyển chọn bài tập trắc nghiệm thể tích khối đa diện

Hình chóp - hình đa diện - khối đa diện

A.Lý thuyết

I.Khối đa diện:

1.Khái niệm:

Hình H cùng với các điểm nằm trong H được họi là khối đa diện giới hạn bởi hình H.

Khối đa diện được giới hạn bởi một hình gồm những đa giác phẳng thỏa mãn hai điều kiện:

* Hai đa giác bất kì hoặc không có điểm chung hoặc có một đỉnh chung hoặc có một cạnh chung

* Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.

2.Khối đa diện đều:

Khối đa diện lồi:

Một khối đa diện được gọi là khối đa diện lồi nếu với bất kì hai điểm \(A\) và \(B\) nào của nó thì mọi điểm thuộc đoạn thẳng \({\rm{AB}}\) cũng thuộc khối đó.

Khối đa diện đều:

Khối đa diện đều là khối đa diện lồi có hai tính chất sau:

* Các mặt là các đa giác đều có cùng số cạnh.

- Mổi đỉnh là đỉnh chung của cùng một số cạnh..

Có đúng 5 loại đa diện đều:

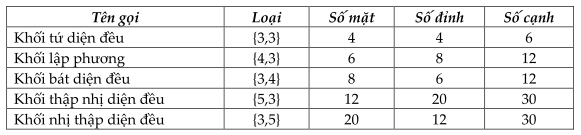
II.Thể tích khối đa diện

1.Thể tích khối chóp:

Thể tích của một khối chóp bằng một phần ba tích số của diện tích đáy và chiều cao của khối chóp đó.

\(V = \frac{1}{3}h \cdot {S_{day}}\)

2. Thể tích lăng trụ - hình hộp:

Thể tích của 1 khối chóp bằng 1 phần ba tích số của diện tích đáy và chiều cao của khối chóp đó

\(V = h.{S_{day}}\)

3. Công thức tỉ số thể tích:

Cho hình chóp S.ABC có \({A^\prime },{B^\prime }\) và \({C^\prime }\) lân lượt nằm trên các cạnh SA, SB và SC. Khi đó tỉ số thể tích giữa khối chóp \({{\rm{S}}^\prime }{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\) và khối chóp S.ABC có công thức:

\(\frac{{{V_{S.{A^\prime }{B^\prime }{C^\prime }}}}}{{{V_{S.ABC}}}} = \frac{{S{A^\prime }}}{{SA}} \cdot \frac{{S{B^\prime }}}{{SB}} \cdot \frac{{S{C^\prime }}}{{SC}}\)

III.Các công thức thường dùng

1.Hệ thức lượng trong tam giác vuông

Cho  vuông tại A, có AH là đường cao, AM là trung tuyến. Khi đó:

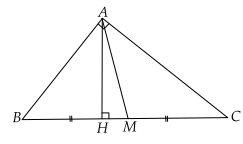
2.Hệ thức lương trong tam giác thường

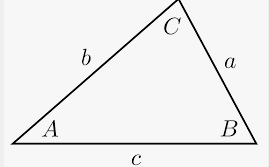
Cho  và đặt \(AB = c,BC = a,CA = b,p = \frac{{a + b + c}}{2}\) (nửa chu vi). Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác ABC. Khi đó:

* Định lý hàm cos:

 \(\left\{ {\begin{array}{*{20}{l}}{{\rm{  -  }}{a^2} = {b^2} + {c^2} - 2bc \cdot \cos A \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}}\\{{\rm{  -  }}{b^2} = {a^2} + {c^2} - 2ac \cdot \cos B \Rightarrow \cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}.}\\{{c^2} = {a^2} + {b^2} - 2ab \cdot \cos C \Rightarrow \cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}}\end{array}} \right.\)

* Định lý hàm sin \[\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\]

* Diện tích tam giác ABC là :

 $\begin{array}{l}=\frac{1}{2}a\cdot h_a=\frac{1}{2}b\cdot h_b=\frac{1}{2}c\cdot h_c\\ =S_{△ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A=\frac{1}{2}ac\sin B\\ S_{△ABC}=\frac{abc}{4R},S_{△ABC}=p\cdot r\\ S_{△ABC}=\sqrt{p\cdot (p-a)\cdot (p-b)\cdot (p-c)},\left(\text{ Héron }\right)\end{array}$

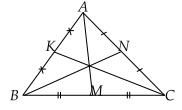
* Công thức trung tuyến : 

\(\left\{ {\begin{array}{*{20}{l}}{{\rm{  -  }}A{M^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4}}\\{ \cdot B{N^2} = \frac{{B{A^2} + B{C^2}}}{2} - \frac{{A{C^2}}}{4}}\\{ - C{K^2} = \frac{{C{A^2} + C{B^2}}}{2} - \frac{{A{B^2}}}{4}}\end{array}} \right.\)

* Định lý Thales

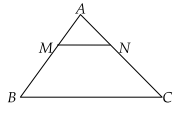
3.Diện tích của đa giác thông thường

* $S_{△\text{ deu }}=\frac{{\left(\mathrm{canh}\right)}^2\cdot \sqrt{3}}{4}$ .

Lưu ý: Chiêu cao trong tam giác đều \(h = \frac{{{\mathop{\rm canh}\nolimits}  \cdot \sqrt 3 }}{2}\).

* S. hình chữ nhật = dài x rộng và S. hình vuông \( = {({\rm{ canh }})^2}\).

Lưu ý: Đường chéo hình vuông = \({\mathop{\rm canh}\nolimits}  \cdot \sqrt 2 \)

* S. hình thang \( = \frac{1}{2}\) (đáy lớn + đáy bé).chiều cao

* S. tứ giác có hai đưòng chéo vuông góc \( = \frac{1}{2}\) tích hai đường chéo

\( \Rightarrow {S_{{\rm{hinh thoi }}}} = \frac{1}{2}\) tích hai đường chéo.

Lưu ý: Trong tính toán diện tích, ta có thể chia đa giác thành những hình đơn giản dễ tính diện tích, sau đó cộng các diện tích được chia này, ta được diện tích đa giác.

4. Xác định chiều cao của hình chóp

a. Hình chóp có một cạnh bên vuông góc với đáy: Chiều cao của hình chóp là độ dài cạnh bên vu n góc với đáy.

Ví dụ: Hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy, tức \(SA \bot (ABC)\) thì chiều cao của hình chóp là SA.

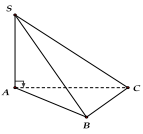
b. Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam giác chứa trong mặt bên vuông góc với đáy.

Ví dụ: Hình chóp S.ABCD có mặt (SAB) vuông góc với mặt phẳng đáy (ABCD) thì chiều cao của hình chóp là SH là chiều cao của .

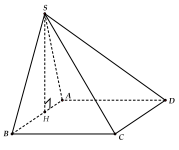
c. Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai mặt b n cùng vuông góc với mặt phẳng đáy.

Ví dụ: Hình chóp S.ABCD có hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy (ABCD) thì chiều cao của hình chóp là SA.

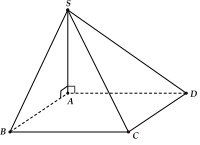
d. Hình chóp đều: Chiêu cao của hình chóp là đoạn thẳng nối đỉnh và tâm của đáy. Đối với hình chóp đều đáy là tam giác thì tâm là trọng tâm G của tam giác đều.

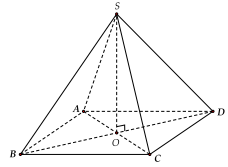
Ví dụ: Hình chóp đều S.ABCD có tâm mặt phẳng đáy là giao điểm của 2 đường chéo hình vuông ABCD thì có đường cao là SO.

B. Trắc nghiệm khách quan

I. Lý thuyết.

Câu 1: Nhận định nào sau đây về số đỉnh hoặc số mặt của một đa diện là nhận định đúng?

A. Lớn hơn hoặc bằng 4 .

B. Lớn hơn 4

C. Lớn hơn hoặc bằng 5 .

D. Lớn hơn 5 .

Câu 2: Nhận định nào sau đây về số cạnh của một đa diện là nhận định đúng?

A. Lớn hơn 4

B. Lớn hơn hoặc bằng 4 .

C. Lớn hơn 6.

D. Lớn hơn hoặc bằng 6 .

Câu 3: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?

A. Hai mặt.

B. Ba mặt.

C. Bốn mặt.

D. Năm mặt.

Câu 4: Khẳng định nào sau đây là khẳng định đúng?

A. Số cạnh của một hình đa diện luôn nhỏ hơn số mặt của hình đa diện ấy.

B. Số cạnh của một hình đa diện luôn lớn hơn số mặt của hình đa diện ấy.

C. Số cạnh của 1 hình đa diện luôn bằng số mặt của hình đa diện ây.

D. Số cạnh của 1 hình đa diện luôn nhỏ hơn hoặc bằng số mặt của hình đa diện ấy.

Câu 5: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng: "Số cạnh của một hình đa điện luôn ................ số đỉnh của hình đa diện ấy".

A. bằng.

B. nhỏ hơn.

C. nhỏ hơn hoặc bằng.

D. lớn hơn.

Câu 6: Cho một hình đa diện. Khẳng định nào sau đây là khẳng định sai?

A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.

B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.

C. Mỗi cạnh là cạnh chung của ít nhất ba mặt.

D. Mỗi mặt có ít nhất ba cạnh.

Câu 7: Có thể chia hình lập phương thành bao nhiêu tứ diện bằng nhau có đỉnh là đỉnh của hình lập phương ?

A. Hai

B. Bốn

C. Sáu

D. Vô số

Câu 8: Số cạnh của một hình bát diện đều là bao nhiêu?

A. 8

B. 10

C. 20

D. 12

Câu 9: Số đỉnh của một hình bát diện đều là bao nhiêu?

A. 6

B. 8

C. 10

D. 12

Câu 10: Số đỉnh của mười hai mặt đều là bao nhiêu ?

A. 12

B. 16

C. 20

D. 30

Câu 11: Số cạnh của một hình mười hai mặt đều là bao nhiêu?

A. 12

B. 16

C. 20

D. 30

Câu 12: Khối đa diện đều loại {4 ; 3} có số đỉnh là bao nhiêu?

A. 4

B. 6

C. 8

D. 10

Câu 13: Khối đa diện đều loại {3 ; 4} có số cạnh là bao nhiêu?

A. 14

B. 12

C. 10

D. 8

Câu 14: Khối đa diện đều loại {5 ; 3} có số mặt là bao nhiêu?

A. 14

B. 12

C. 10

D. 8

Câu 15: Khối lập phương là khối đa diện đều loại nào

A. {5;3}

B. {3;4}.

C. {4;3}.

D. 8

Câu 16: Có bao nhiêu loại khối đa diện đều?

A. 3

B. 5

C. 20

D. Vô số.

Câu 17: Khối mười hai mặt đều thuộc loại nào?

A. {5;3}.

B. {3;5}.

C. {4;3}.

D. {3;4}.

Câu 18: Chọn khẳng định đúng nhất: Kim Tự Tháp ở Ai Cập có hình dáng của khối đa diện nào sau đây?

A. Khối chóp tam giác đều.

B. Khối chóp tứ giác.

C. Khối chóp tam giác.

D. Khối chóp tứ giác đều.

Câu 19: Mỗi đỉnh của bát diện đều là đỉnh chung của bao nhiêu mặt?

A. 3

B. 4

C. 5

D. 8

Câu 20: Khối chóp đều S.ABCD có mặt đáy là hình gì?

A. Hình bình hành.

B. Hình chữ nhật.

C. Hình thoi.

D. Hình vuông.

Câu 21: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?

A. 2

B. 3

C. 4

D. 5

Câu 22: Hình lập phương có bao nhiêu mặt phẳng đối xứng?

A. 6

B. 7

C. 8

D. 9

Câu 23: Tứ diện đều có bao nhiêu mặt phẳng đối xứng?

A. 4

B. 6

C. 8

D. 10

Câu 24: Khối lập phương có bao nhiêu mặt?

A. 4

B. 6

C. 8

D. 10

Câu 25: Khẳng định nào sau đây là khẳng định sai?

A. Tồn tại một hình đa diện có số đỉnh nhỏ hơn số mặt.

B. Tồn tại một hình đa diện có số đỉnh và số mặt bằng nhau.

C. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.

D. Tồn tại một hình đa diện có số cạnh và số mặt bằng nhau.

Câu 26: Khẳng định nào sau đây là khẳng định đúng?

A. Ghép 2 khối chóp tứ giác đều ta được một khối bát diện đều.

B. Ghép 2 khối chóp tam giác đều ta được một khối bát diện đều.

C. Ghép 2 khối chóp tứ giác đều có các cạnh bằng nhau ta được một khối bát diện đều.

D. Ghép 2 khối tứ diện đều ta được một khối bát diện đều.

Câu 27: Khẳng định nào sau đây là khẳng định đúng?

A. Chỉ tồn tại 4 loại đa diện đều

B. Chỉ tồn tại 5 loại đa diện đều.

C. Chỉ tồn tại 6 loại đa điện đều.

D. Tồn tại vô số loại đa diện đều.

Câu 28: Khẳng định nào sau đây là khẳng định sai?

A. Lắp ghép hai khối tứ diện đều bằng nhau sao cho hai tứ diện có một mặt chung thì ta được một khối đa diện lôi.

B. Lắp ghép hai khối chóp tứ giác đều bằng nhau sao cho hai hình chóp có một mặt chung thì ta được một khối đa diện lồi.

C. Lắp ghép hai khối lăng trụ bằng nhau sao cho hai lăng trụ có một mặt chung thì ta được một khối đa diện lồi.

D. Lắp ghép hai khối lập phương bằng nhau sao cho hai hình lập phương có một mặt chung thì ta được một khối đa diện lồi.

Câu 29: Cho tứ diện đều ABCD có M, N, P, Q, R, S lần lượt là trung điểm các cạnh của tứ diện. Khẳng định nào sau đây là khẳng định sai?

A. MNPQRS là một bát diện đều.

B. MNPQR là một hình chóp tứ giác đều.

C. MNPQ là một tứ diện đều.

D. . MNPQ là một hình chóp tứ diện đều.