Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các phương pháp tính thể tích khối đa diện, tài liệu bao gồm 34 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Các phương pháp tính thể tích khối đa diện

Chuyên đề: Phương pháp luyện tập thế tích khối đa diện

I. Ôn tập kiến thức cơ bản:

Ôn tập 1. Kiến thức cơ bản hình học lớp 9 - 10

1. Hệ thức lượng trong tam giác vuông : Cho  vuông ở A ta có :

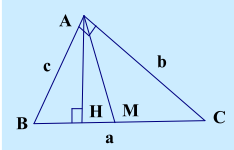
a) Định lý Pitago : \(B{C^2} = A{B^2} + A{C^2}\)

b) \(B{A^2} = BH \cdot BC;C{A^2} = CH \cdot CB\)

c) \({\rm{AB}} \cdot {\rm{AC}} = {\rm{BC}} \cdot {\rm{AH}}\)

d) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)

e) \({\rm{BC}} = 2{\rm{AM}}\)

f) \(\sin B = \frac{b}{a},\cos B = \frac{c}{a},\tan B = \frac{b}{c},\cot B = \frac{c}{b}\)

g) \({\rm{b}} = {\rm{a}} \cdot \sin {\rm{B}} = {\rm{a}} \cdot \cos {\rm{C}},{\rm{c}} = {\rm{a}} \cdot \sin {\rm{C}} = {\rm{a}} \cdot \cos {\rm{B}},\)

\({\rm{a}} = \frac{b}{{\sin B}} = \frac{b}{{\cos C}},b = c \cdot \tan B = c \cdot \cot C\)

2. Hệ thức lượng trong tam giác thường

* Định lý hàm số Coosin :

\[{a^2} = {b^2} + {c^2} - 2bc \cdot \cos A\]

* Định lý hàm số Sin:

\[\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\]

3. Các công thức tính diện tích

a) Công thức tính diện tích tam giác

\(\begin{array}{l}S = \frac{1}{2}a \cdot {h_{\rm{a}}} = \frac{1}{2}a \cdot b\sin C = \frac{{a \cdot b \cdot c}}{{4R}} = p \cdot r\\ = \sqrt {p \cdot (p - a)(p - b)(p - c)} {\rm{ }}\end{array}\)

Với p \( = \frac{{a + b + c}}{2}\)

Đặc biệt

*∆ABC vuông ở A : \(S = \frac{1}{2}AB \cdot AC\),

*∆ABC  đều cạnh a: \(S = \frac{{{a^2}\sqrt 3 }}{4}\)

b/ Diện tích hình vuông : S = cạnh x cạnh

c/ Diện tích hình chữ nhât : S = dài x rộng

\({\rm{d}}\) / Diên tích hình thoi : \({\rm{S}} = \frac{1}{2}\) (chéo dài x chéo ngắn)

d/ Diện tích hình thang: \({\rm{S}} = \frac{1}{2}\)( đáy lớn + đáy nhỏ ) x chiều cao

e/ Diện tích hình bình hành : S =  đáy X chiều cao

f/ Diện tích hình tròn : \({\rm{S}} = \pi  \cdot {R^2}\)

Ôn tập 2 Kiến thức cơ bản hình học lớp 11

A. Quan hệ song song

§1. Đường thẳng và mặt phẳng song song

I. Định nghĩa:

Đường thẳng và mặt phẳng gọi là song song với nhau nếu chúng không có điểm nào chung.

\({\rm{a}}//({\rm{P}}) \Leftrightarrow {\rm{a}} \cap ({\rm{P}}) = \emptyset \)

II.Các định lý:

ĐL1: Nếu đường thẳng d không nằm trên mp(P) và song song vói đường thẳng a nằm trên mp(P) thì đường thẳng d song song với mp(P)

\(\left\{ {\begin{array}{*{20}{l}}{{\rm{d}}\not  \subset ({\rm{P}})}\\{{\rm{d}}//{\rm{a}}}\\{{\rm{a}} \subset ({\rm{P}})}\end{array} \Rightarrow {\rm{d}}//({\rm{P}})} \right.\)

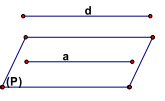
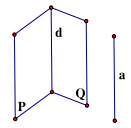
ĐL2: Nếu đường thẳng a song song với mp(P) thì mọi mp(Q) chứa a mà cắt mp(P) thì cắt theo giao tuyến song song với a.

\(\left\{ {\begin{array}{*{20}{l}}{{\rm{a}}//({\rm{P}})}\\{{\rm{a}} \subset ({\rm{Q}})}\\{({\rm{P}}) \cap ({\rm{Q}}) = {\rm{d}}}\end{array} \Rightarrow {\rm{d}}//{\rm{a}}} \right.\)

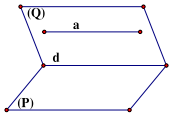
ĐL3: Nếu hai mặt phẳng cắt nhau cùng song song với với 1 đưởng thẳng thì giao tuyến của chúng song song với đường thẳng đó.

\[\left\{ {\begin{array}{*{20}{l}}{({\rm{P}}) \cap ({\rm{Q}}) = {\rm{d}}}\\{({\rm{P}})//{\rm{a}}}\\{({\rm{Q}})//{\rm{a}}}\end{array} \Rightarrow {\rm{d}}//{\rm{a}}} \right.\]

§2. Hai mặt phẳng song song

I. Định nghĩa:

Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm nào chung.

\(({\rm{P}})//({\rm{Q}}) \Leftrightarrow ({\rm{P}}) \cap ({\rm{Q}}) = \emptyset \)

II.Các định lý:

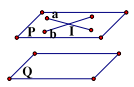
ĐL1: Nếu mp(P) chứa hai đường thẳng a,b cắt nhau và cùng song song vói mặt phẳng (Q) thì (P) và (Q) song song với nhau.

\(\left\{ {\begin{array}{*{20}{l}}{{\rm{a}},{\rm{b}} \subset ({\rm{P}})}\\{{\rm{a}} \cap {\rm{b}} = {\rm{I}}}\\{{\rm{a}}//({\rm{Q}}),{\rm{b}}//({\rm{Q}})}\end{array} \Rightarrow ({\rm{P}})//({\rm{Q}})} \right.\)

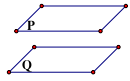
ĐL2: Nếu 1 đưởng thẳng nằm 1 trong hai mặt phẳng song song thì song song với mặt phẳng kia.

\(\left\{ {\begin{array}{*{20}{l}}{({\rm{P}})//({\rm{Q}})}\\{{\rm{a}} \subset ({\rm{P}})}\end{array} \Rightarrow {\rm{a}}//({\rm{Q}})} \right.\)

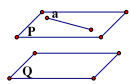
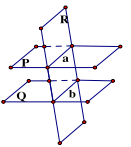
ĐL3: Nếu hai mặt phẳng (P) và (Q) song song thì mọi mặt phẳng (R) đã cắt (P) thì phải cắt (Q) và các giao tuyến của chúng song song.

\(\left\{ {\begin{array}{*{20}{l}}{({\rm{P}})//({\rm{Q}})}\\{({\rm{R}}) \cap ({\rm{P}}) = {\rm{a}} \Rightarrow {\rm{a}}//{\rm{b}}}\\{({\rm{R}}) \cap ({\rm{Q}}) = {\rm{b}}}\end{array}} \right.\)

B. Quan hệ vuông góc

§1. Đường thẳng vuông góc với mặt phẳng

I. Định nghĩa:

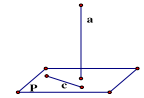
Một đường thẳng được gọi là vuông góc với 1 mặt phẳng nếu nó vuông góc vói mọi đường thẳng nằm trên mặt phẳng đó.

\({\rm{a}} \bot {\rm{mp}}({\rm{P}}) \Leftrightarrow {\rm{a}} \bot {\rm{c}},\forall {\rm{c}} \subset ({\rm{P}})\)

II. Các định lý:

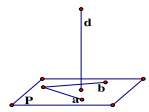
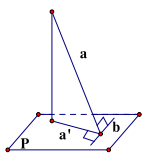
ĐL 1: Ba đường vuông góc. Cho đường thẳng a không vuông góc với mp(P) và đường thẳng b nằm trong (P). Khi đó, điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P).

\(\left\{ {\begin{array}{*{20}{l}}{{\rm{d}} \bot {\rm{a}},{\rm{d}} \bot {\rm{b}}}\\{{\rm{a}},{\rm{b}} \subset {\rm{mp}}({\rm{P}}) \Rightarrow {\rm{d}} \bot {\rm{mp}}({\rm{P}})}\\{{\rm{a}},{\rm{b cat nhau }}}\end{array}} \right.\)

ĐL2: (Ba đường vuông góc) Cho đường thẳng a không vuông góc với mp(P) và đường thẳng b nằm trong (P). Khi đó, điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P).

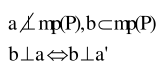
§2. Hai mặt phẳng vuông góc

I. Định nghĩa:

Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^^\circ }\).

II. Các định lý:

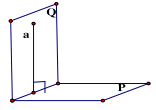
ĐL1: Nếu 1 mặt phẳng chứa 1 đường thẳng vuông góc vói 1 mặt phẳng khác thì hai mặt phẳng đó vuông góc với nhau.

\(\left\{ {\begin{array}{*{20}{l}}{{\rm{a}} \bot {\rm{mp}}({\rm{P}})}\\{{\rm{a}} \subset {\rm{mp}}({\rm{Q}})}\end{array} \Rightarrow {\rm{mp}}({\rm{Q}}) \bot {\rm{mp}}({\rm{P}})} \right.\)

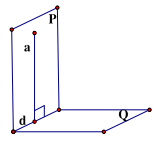
ĐL2: Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau thì bất cứ đường thẳng a nào nằm trong (P), vuông góc với giao tuyến của (P) và (Q) đều vuông góc với mặt phẳng (Q).

\(\left\{ {\begin{array}{*{20}{l}}{({\rm{P}}) \bot ({\rm{Q}})}\\{{\rm{P}}) \cap ({\rm{Q}}) = {\rm{d}} \Rightarrow {\rm{P}}),{\rm{a}} \bot {\rm{d}}}\end{array}} \right.\)

ĐL3: Nếu hai mặt phẳng (P) và (Q) vuông góc vói nhau và A là 1 điểm trong (P) thì đường thẳng a đi qua điểm A và vuông góc với (Q) sẽ nẳm trong (P)

\(\left\{ {\begin{array}{*{20}{l}}{{\rm{A}} \in ({\rm{Q}})}\\{{\rm{A}} \in {\rm{P}}) \bot ({\rm{P}})}\\{{\rm{a}} \bot ({\rm{Q}})}\end{array} \Rightarrow {\rm{a}} \subset ({\rm{P}})} \right.\)

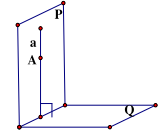
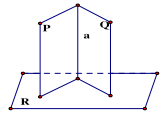
ĐL4: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

\(\left\{ {\begin{array}{*{20}{l}}{({\rm{P}}) \cap ({\rm{Q}}) = {\rm{a}}}\\{({\rm{P}}) \bot ({\rm{R}})}\\{({\rm{Q}}) \bot ({\rm{R}})}\end{array} \Rightarrow {\rm{a}} \bot ({\rm{R}})} \right.\)

§3. Khoảng cách

1. Khoảng cách từ 1 điểm tới 1 đường thẳng, đến 1 mặt phẳng:

Khoảng cách từ điểm M đến đường thẳng a ( hoặc đến mặt phẳng (P) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên đường thẳng a ( hoặc trên mp(P))

D(O;a) = OH; d(O;(P)) = OH

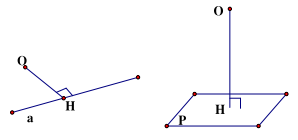
2. Khoảng cách giữa đường thắng và mặt phẳng song song:

Khoảng cách giữa đường thẳng a và mp(P) song song với a là khoảng cách từ một điểm nào đó của a đến mp(P).

d(a;(P)) = OH

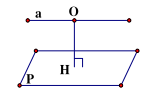
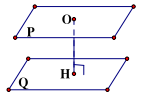
3. Khoảng cách giữa hai mặt phẳng song song:

là khoảng cách từ một điểm bất kỳ trên mặt phẳng này đến mặt phẳng kia.

 d((P);(Q)) = OH

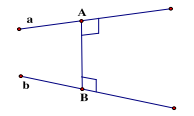
4. Khoảng cách giữa hai đường thẳng chéo nhau:

là độ dài đoạn vuông góc chung của hai đường thẳng đó.

d(a,b) = AB

§4. Góc

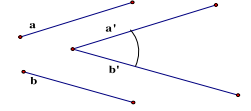
1. Góc giữa hai đường thẳng a và b là góc giữa hai đường thẳng a' và b' cùng đi qua một điểm và lần lượt cùng phương với a và b.

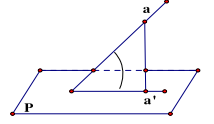
2. Góc giữa đường thẳng a không vuông góc với mặt phẳng (P) là góc giữa a và hình chiếu a' của nó trên mp(P).

Đặc biệt: Nếu a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mp(P) là \({90^ \circ }\).

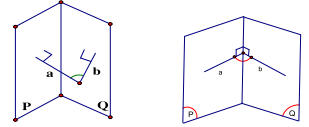
3. Góc giữa hai măt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Hoặc là góc giữa 2 đường thẳng nằm trong 2 mặt phẳng cùng vuông góc với giao tuyến tại 1 điểm.