Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển chọn bài tập trắc nghiệm hình trụ - khối trụ, tài liệu bao gồm 36 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tuyển chọn bài tập trắc nghiệm hình trụ - khối trụ

Phần 1: Hình trụ tròn xoay – khối trụ tròn xoay

A. Hình trụ tròn xoay

Xây dựng:

Khi quay hình chữ nhật ABCD xung quang đường thẳng chứa cạnh AB thì ta được 1 hình được gọi là hình trụ tròn xoay hay hình trụ.

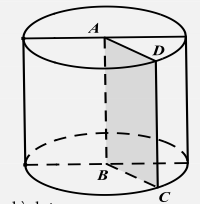
Đường thẳng AB là………..

Đường thẳng CD là…………….

Độ dài đoạn thẳng AB = CD = h gọi là …………. của hình trụ

Hình tròn tâm A, bán hính r = AD và hình tròn tâm B, bán kính r = BC được gọi là……….

B. Khối trụ tròn xoay: Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không gian giói hạn bởi hình trụ tròn xoay kể cả hình trụ.

C. Công thức tính diện tích hình trụ và thể tích của khối trụ

Cho hình trụ có chiều cao là h và bán kính đáy bằng r, khi đó

- Diện tích xung quanh:

- Diện tích toàn phần

Thể tích khối trụ

Ví dụ 01 : Cho hình trụ (T) có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu \({S_{xq}}\) là diện tích xung quanh của (T). Công thức nào sau đây là đúng?

A. \({S_{xq}} = \pi rh\).

B. \({S_{xq}} = 2\pi rl\).

C. \({S_{xq}} = 2\pi {r^2}h.\)

D. \({S_{xq}} = \pi rl\).

Ví dụ 02 : Cho hình trụ (T) có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu \({S_{tp}}\) là diện tích toàn phần của (T). Công thức nào sau đây là đúng?

A. \({S_{tp}} = \pi rl\)

B. \({S_{tp}} = \pi rl + 2\pi r\)

C. \({S_{tp}} = \pi rl + \pi {r^2}\)

D. \({S_{tp}} = 2\pi rl + 2\pi {r^2}\)

Ví dụ 03 : Cho hình trụ (T) có chiều cao h, độ dài đường sinh \(l\), bán kính đáy r. Ký hiệu \({V_{(T)}}\) là thể tích khôi trụ (T). Công thức nào sau đây là đúng?

A. \({V_{(T)}} = \frac{1}{3}\pi rh\)

B. \({V_{(T)}} = \pi {r^2}h\)

C. \({V_{(N)}} = \pi r{l^2}\)

D. \({V_{(N)}} = 2\pi {r^2}h\)

Ví dụ 04 : Một hình trụ có bán kính đáy r = 5cm, chiều cao h = 7cm. Diện tích xung quanh của hình trụ này là:

A. \(35\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

B. \(70\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

C. \(\frac{{70}}{3}\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

D. \(\frac{{35}}{3}\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

Ví dụ 05 : Một hình trụ có bán kính đáy r = a, đồ dài đường sinh l = 2a. Diện tích toàn phần của hình trụ này là:

A. \(6\pi {a^2}\)

B. \(2\pi {a^2}\)

C. \(4\pi {a^2}\)

D. \(5\pi {a^2}\)

Ví dụ 06 (THPT Nguyễn Tất Thành) : Cho khối trụ có bán kính \(a\sqrt 3 \) và chiều cao \(2a\sqrt 3 \). Thể tích của khối trụ đó là :

A. \(9{a^3}\sqrt 3 \)

B. \(6\pi {a^3}\sqrt 3 \)

C. \(6\pi {a^2}\sqrt 3 \)

D. \(4\pi {a^3}\sqrt 2 \)

Ví dụ 07 (THPT Chuyên Thái Bình) : Cho khối trụ (T) có bán kính đáy R và diện tích toàn phần \(8\pi {R^2}\). Tính thể tích của khôi trụ (T).

A. \(6\pi {R^3}\)

B. \(8\pi {R^3}\)

C. \(4\pi {R^3}\)

D. \(3\pi {R^3}\)

Bài tập mẫu có giải tham khảo

Bài 01 : Cho hình trụ có diện tích xung quanh bằng \(50\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\) và thể tích khối trụ tương ứng bằng \(100\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\). Tính độ dài bán kính đáy r của hình trụ đã cho.

A. \(r = 2(\;{\rm{cm}})\)

B. \(r = 4(\;{\rm{cm}})\)

C. \(r = 6(\;{\rm{cm}})\)

D. \(r = 12(\;{\rm{cm}})\)

Giải : Gọi h là chiều cao của hình trụ

Ta có \(\left\{ {\begin{array}{*{20}{l}}{{S_{xq}} = 2\pi rh = 50}\\{V = \pi {r^2}h = 100(2)}\end{array}} \right.\)

Lấy (2) chia (1) theo vế ta được : \(\frac{{(2)}}{{(1)}} = \frac{r}{2} = \frac{{100}}{{50}} \Rightarrow r = 4(\;{\rm{cm}})\)

Ta chọn đáp án B

Bài 02 (THPT Thuận Thành) : Trong không gian, cho hình chữ nhật ABCD có \(AB = 3a,BD = 5a\).Tính độ dài đường sinh l của hình trụ nhận được khi quay hình chữ nhật ABCD quanh trục AD.

A. \(l = 5a\)

B. \(l = 4a\)

C. \(l = 3a\)

D. \(l = 2\sqrt 2 a\)

(-) Giải : Quay hình chữ nhật quanh AD thì đường sinh là l = BC.

\( \Rightarrow BC = AD = \sqrt {B{D^2} - A{B^2}}  = 4a;\) Ta chọn đáp án B

Bài 03 (THPT Thuận Thành 2) : Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a\((\)a là độ dài cho sẵn) . Người ta cuốn tấm nhôm đó thành 1 hình trụ. Nếu hình trụ được tạo thành có chiều dài đường dinh bằng 2a thì bán kính đáy r bằng.

A. \(r = \frac{a}{\pi }\)

B. \(r = \frac{a}{{2\pi }}\)

C. \(r = \frac{a}{2}\)

D. \(r = 2\pi a\)

(-) Giải : Hình trụ tạo thành có đường \(\sinh l = 2a\) nên chiều rộng a của hình chữ nhật sẽ cuốn cong lại hay đó là chu vi của đường tròn đáy của hình trụ

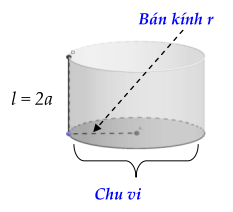
Ta có: \(2\pi r = a \Rightarrow r = \frac{a}{{2\pi }};\)

Ta chọn đáp án B

Bài 04 (THPT Lê Hồng Phong - Nam Định) : Một cái cốc hình trụ cao 15cm đựng được 0,5 lít nước. Hỏi bán kính đường tròng đáy của cái cốc sấp sỉ bằng bao nhiêu (làm tròn đến hàng thập phân thứ hai)?

A. \(3,27\;{\rm{cm}}\)

B. \(3,26\;{\rm{cm}}\)

C. \(3,25\;{\rm{cm}}\)

D. \(3,28\;{\rm{cm}}\)

(-) Giải : Theo công thức thể tích hình trụ

\(V = \pi {R^2}h \Rightarrow {R^2} = \frac{V}{{\pi h}} \Rightarrow R = \sqrt {\frac{V}{{\pi h}}} \)

Với

\(\begin{array}{l}h = 15\;{\rm{cm}},V = 0,5l = 0,5 \cdot 1000\;{\rm{c}}{{\rm{m}}^3} = 500\;{\rm{c}}{{\rm{m}}^3}\\ \Rightarrow R = \sqrt {\frac{{500}}{{\pi  \cdot 15}}}  \approx 3,26\;{\rm{cm}}\end{array}\)

Ta chọn đáp án B

Bài 05 : Diện tích xung quanh của một hình trụ bằng \(24\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\) và diện tích toàn phần bằng \(42\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\). Tính chiều cao h(cm) của hình trụ.

A. \(h = 6\)

B. \(h = 4\)

C. \(h = 3\)

D. \(h = 12\)

Giải: Ta có:

\(\begin{array}{l}{S_{tp}} = {S_{xq}} + 2{S_d} \Leftrightarrow 42\pi  = 24\pi  + 2\pi {R^2}\\ \Leftrightarrow {R^2} = 9 \Leftrightarrow R = 3\end{array}\).

Mặt khác

\(\begin{array}{l}{S_{xq}} = 24\pi  \Leftrightarrow 2\pi {\rm{R}}h = 24\pi  \Leftrightarrow Rh = 12\\ \Leftrightarrow h = \frac{{12}}{R} = \frac{{12}}{3} = 4(\;{\rm{cm}})\end{array}\)

Ta chọn đáp án B

Bài 06 (THPT Lương Tài 2) : Trong không gian cho hình vuông ABCD có cạnh bằng 4 . Quay hình vuông đó xung quanh trục AB, ta nhận được một hình trụ. Tính diện tích toàn phần \({S_{tp}}\) của hình trụ đó.

A. \(80\pi \)

B. \({S_{tp}} = 32\pi \)

C. \({S_{tp}} = 64\pi \)

D. \({S_{tp}} = 48\pi \)

Giải:

\({S_{tp}} = 2\pi {R^2} + 2\pi Rh = 4\pi {R^2} = 4\pi {4^2} = 64\pi \)

Ta chọn đáp án C

Bài 07 (THPT Chuyên ĐH Vinh) : Một khối trụ có thể tích bằng \(16\pi \). Nếu chiều cao của khối trụ tăng lên 2 lần và giữ nguyên bán kính đáy thì được 1 khối trụ mới có diện tích xung quanh bằng \(16\pi \). Bán kính đáy của khối trụ ban đầu bằng?

A. 8

B. 1

C. 4

D. 2

(-) Giải : Gọi chiều cao ban đầu của khối trụ là \({h_1}\), chiêu cao của khối trụ sau tăng là \({h_2}\); khi đó \({h_2} = 2{h_1}.\)

Theo đề \(:V = \pi  \cdot {R^2} \cdot {h_1} = 16\pi ;{S_{xq}} = 2\pi R \cdot {h_2} = 2\pi R \cdot 2{h_1} = 16\pi \).

Chia vế theo vế hai đẳng thức:

\( \Rightarrow \frac{R}{4} = 1 \Rightarrow R = 4{\rm{;}}\)

Ta chọn đáp án C

Bài 8 (THPT Gia Lộc 2): Cho hình vuông ABCD biết cạnh bằng a. Gọi I, K lần lượt là trung điểm của BCD. Tính diện tích xung quanh của hình trụ tròn xoay khi cho hình vuông ABCD quay quanh IK một góc ${360}^o$.

A. \(\frac{{\pi {a^2}}}{3}\)

B. \(\pi {a^2}\)

C. \(2\pi {a^2}\)

D. \(\frac{{2\pi {a^2}}}{3}\)

(-) Giải:

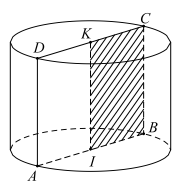
 Hình trụ có đường sinh l = BC = a

Bán kính đáy \(r = IB = \frac{a}{2}\).

Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi rl = \pi {a^2}\);

Ta chọn đáp án B

Bài 09 (THPT Nguyễn Trãi lần 1) : Cho hình lập phương \(ABCD \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) có cạnh bằng a . Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và \({{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\). Tính S.

A. \(\frac{{\pi {a^2}\sqrt 2 }}{2}\)

B. \(\pi {a^2}\sqrt 2 \)

C. \(\pi {a^2}\sqrt 3 \)

D. \(\pi {a^2}\)

Giải

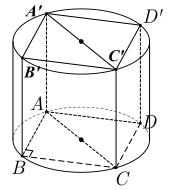
Gọi R;h lân lượt là bán kính của đường tròn đáy và chiểu cao của khối trụ.

Ta có ABCD là hình vuông nên \(R = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\) \(h = {\rm{A}}{{\rm{A}}^\prime } = {\rm{a}}.\)

Khi đó: \({V_T} = \pi  \cdot {R^2} \cdot h = \pi  \cdot \frac{{{a^2}}}{2} \cdot a = \frac{{\pi {a^3}}}{2};\) Ta chọn đáp án B