Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 3 Bài 5:Giải bài toán bằng cách lập hệ phương trình . Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 5: Giải bài toán bằng cách lập hệ phương trình. Mời các bạn đón xem:
Bài tập Toán 9 Chương 3 Bài 5: Giải hệ phương trình bằng phương pháp cộng đại số
A. Bài tập Giải bài toán bằng cách lập hệ phương trình
I. Bài tập trắc nghiệm
Câu 1: Cho hệ phương trình 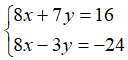
Chọn đáp án A
Câu 2: Cho hệ phương trình 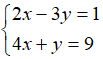
A. x - y = -1
B. x - y = 1
C. x - y = 0
D. x - y = 2
Chọn đáp án B
Câu 3: Cho hệ phương trình 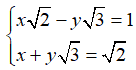
Chọn đáp án D
Câu 4: Cho hệ phương trình 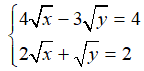
A. 2
B. 0
C. -2
D. 1
Chọn đáp án B
Câu 5: Cho hệ phương trình 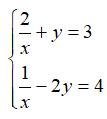
A. 2
B. -2
C. -1/2
D. 1/2
Chọn đáp án C
Câu 6: Giải hệ phương trình:
A. (2; 1)
B. (3; -1)
C. ( -2; 1)
D. (0; 2)
Vậy nghiệm của hệ phương trình đã cho là: (2; 1)
Chọn đáp án A.
Câu 7: Xác định hệ số a và b để đồ thị hàm số y = ax + b đi qua điểm A(2; 0) và B (-1; 3) ?
A. a = 1; b = -2
B. a = -1; b = 2
C. a = 1; b = 2
D. a = -1; b = -2
Do đồ thị hàm số đã cho đi qua hai điểm A và B nên ta có:
Chọn đáp án B.
Câu 8: Giải hệ phương trình:
A. (3 ; 2)
B. (1; -3)
C. ( -2; 1)
D. (1; 3)
Vậy nghiệm của hệ phương trình đã cho là (-2; 1)
Chọn đáp án C.
Câu 9: Cho hệ phương trình 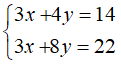
A. 8
B. 5
C. 10
D. 17
Chọn đáp án A.
Câu 10: Giải hệ phương trình:
A.( 3; 2)
B.(3; 3)
C. ( 0; 6)
D. ( 0; 3).
Vậy nghiệm của phương trình đã cho là (0; 3).
Chọn đáp án D.
Câu 11: Số nghiệm của hệ phương trình 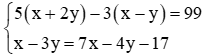
A. 2
B. Vô số
C. 1
D. 0
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (4;7)
Đáp án cần chọn là: C
Câu 12: Số nghiệm của hệ phương trình 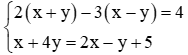
A. 2
B. Vô số
C. 1
D. 0
Vậy hệ phương trình vô nghiệm
Đáp án cần chọn là: D
Câu 13: Kết luận nào đúng khi nói về nghiệm (x;y) của hệ phương trình
A. x > 0; y < 0
B. x < 0; y < 0
C. x < 0; y > 0
D. x > 0; y > 0
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (31; −3)
⇒ x > 0; y < 0
Đáp án cần chọn là: A
Câu 14: Kết luận nào đúng khi nói về nghiệm (x; y) của hệ phương trình
A. x > 0; y < 0
B. x < 0; y < 0
C. x < 0; y > 0
D. x > 0; y > 0
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (2; 8)
Đáp án cần chọn là: D
Câu 15: Hệ phương trình 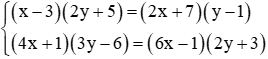
Lời giải:
Đáp án cần chọn là: B
II. Bài tập tự luận có lời giải
Câu 1: Giải hệ phương trình sau
Lời giải:
Cộng từng vế của hai phương trình trong hệ (I) ta được: 4x = 4
Do đó ta có hệ:
Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (1; -1).
Câu 2: Giải hệ phương trình sau:
Lời giải:
Nhân cả hai vế của phương trình thứ nhất với 2, khi đó ta được hệ tương đương:
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x; y) = (2; 1).
III. Bài tập vận dụng
Câu 1: Giải hệ phương trình sau bằng phương pháp cộng đại số
Câu 2: Giải hệ phương trình
B. Lý thuyết Giải bài toán bằng cách lập hệ phương trình
Các bước giải bài toán bằng cách lập phương trình
Bước 1: Lập phương trình
- Chọn ẩn và đặt điều kiện thích hợp cho chúng
- Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình nói trên.
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện và kết luận.









