Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập về tỉ số thể tích khối đa diện, tài liệu bao gồm 15 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập về tỉ số thể tích khối đa diện

Tỷ số thể tích khối đa diẹn

I- Phương pháp

Kết quả 1: Cho tam giác OAB, trên cạnh OA chọn \({A^\prime } \ne O\), trên cạnh OB chọn \({B^\prime } \ne O\).

Lúc đó: \(\frac{{{S_{O{A^\prime }{B^\prime }}}}}{{{S_{OAB}}}} = \frac{{O{A^\prime }}}{{OA}} \cdot \frac{{O{B^\prime }}}{{OB}}\)

Chứng minh:

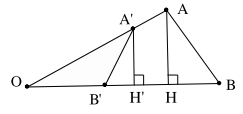
Gọi \({\rm{H}},{{\rm{H}}^\prime }\) lần lượt là hình chiếu vuông góc của A và \({{\rm{A}}^\prime }\) lên OB.

Lúc đó: \({S_{O{A^\prime }{B^\prime }}} = \frac{1}{2}{A^\prime }{H^\prime }.O{B^\prime }\) và \({S_{OAB}} = \frac{1}{2}AH.OB\)

Suy ra:

\(\frac{{{S_{O{A^\prime }{B^\prime }}}}}{{{S_{OAB}}}} = \frac{{{A^\prime }{H^\prime }}}{{AH}} \cdot \frac{{O{B^\prime }}}{{OB}} = \frac{{O{A^\prime }}}{{OA}} \cdot \frac{{O{B^\prime }}}{{OB}}{\rm{ }}\)(Định lý thales)

Kết quả 2:

Cho hình chóp S.ABC, trên cạnh SA chọn \({A^\prime } \ne O\), trên cạnh SB chọn \({B^\prime } \ne O\) trên cạnh SC chọn \({C^\prime } \ne O\).

Lúc đó:

\(\frac{{{V_{S.{A^\prime }{B^\prime }{C^\prime }}}}}{{{V_{S.ABC}}}} = \frac{{S{A^\prime }}}{{SA}} \cdot \frac{{S{B^\prime }}}{{SB}} \cdot \frac{{S{C^\prime }}}{{SC}}\)

Chứng minh:

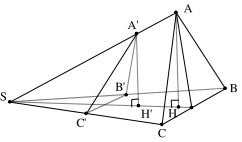
Gọi \({\rm{H}},{{\rm{H}}^\prime }\) lần lượt là hình chiếu vuông góc của A và \({{\rm{A}}^\prime }\) lên mp (SBC)

Lúc đó:

\({V_{S.{A^\prime }{B^\prime }{C^\prime }}} = \frac{1}{3}{A^\prime }{H^\prime }.{S_{S{B^\prime }{C^\prime }}}{\rm{ v\`a  }}{{\rm{V}}_{S.ABC}} = \frac{1}{3}AH.{S_{SBC}}\)

Suy ra:

II- Bài tập trắc nghiệm minh họa

Ví dụ 1: Cho hình lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\). Tỉ số thể tích của khối \(A{A^\prime }{B^\prime }{C^\prime }\) và khối \(ABC{C^\prime }\) là

A. 1 .

B. \(\frac{1}{2}\).

C. \(\frac{1}{3}\).

D. \(\frac{2}{3}\).

Lời giải

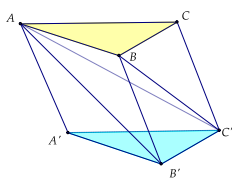
Ta có: \(\frac{{{V_{A{A^\prime }{B^\prime }{C^\prime }}}}}{{{V_{{C^\prime }ABC}}}} = \frac{{\frac{1}{3}d\left( {A;\left( {{A^\prime }{B^\prime }{C^\prime }} \right)} \right) \cdot {S_{{A^\prime }{B^\prime }{C^\prime }}}}}{{\frac{1}{3}d(C;(ABC)) \cdot {S_{ABC}}}}(1)\)

Do \({S_{ABC}} = {S_{{A^\prime }{B^\prime }{C^\prime }}}\) và \(d\left( {A;\left( {{A^\prime }{B^\prime }{C^\prime }} \right)} \right) = d(C;(ABC))\)

nên (1): \(\frac{{{V_{A{A^\prime }{B^\prime }{C^\prime }}}}}{{{V_{{C^\prime }ABC}}}} = 1\).

\( \Rightarrow \) Chọn đáp án A.

Ví dụ 2: Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SB, SD. Mặt phẳng (AMN) cắt SC tại E. Gọi \({V_2}\) là thể tích của khối chóp S.AMEN và \({V_1}\) là thể tích khối chóp S.ABCD. Khẳng định nào sau đây đúng?

A. \({V_2} = \frac{1}{3}{V_1}.\)

B. \({V_2} = \frac{1}{4}{V_1}\)

C. \({V_2} = \frac{1}{8}{V_1}\).

D. \({V_2} = \frac{1}{6}{V_1}\).

Lời giải

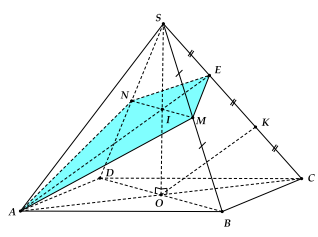
\(\frac{{SM}}{{SB}} = \frac{{SN}}{{SD}} = \frac{{SI}}{{SO}} = \frac{1}{2} \to Qua\) O dụng \(OK//AE.\)

Xét  điểm EC.

Xét

 Suy ra: E là trung điểm SK. Vậy \(\frac{{SE}}{{SC}} = \frac{1}{3}\)

Ta có:

\[\begin{array}{l}\frac{{{V_{S.AMEN}}}}{{{V_{S.ABCD}}}} = \frac{{2{V_{S.AME}}}}{{2{V_{S.ABC}}}}\\ = \frac{{SA}}{{SA}} \cdot \frac{{SM}}{{SB}} \cdot \frac{{SE}}{{SC}} = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}\end{array}\]

\( \Rightarrow {V_{S.AMEN}} = \frac{1}{6}{V_{S.ABCD}}\) hay \({V_2} = \frac{1}{6}{V_1}\).

\( \Rightarrow \) Chọn đáp án D.

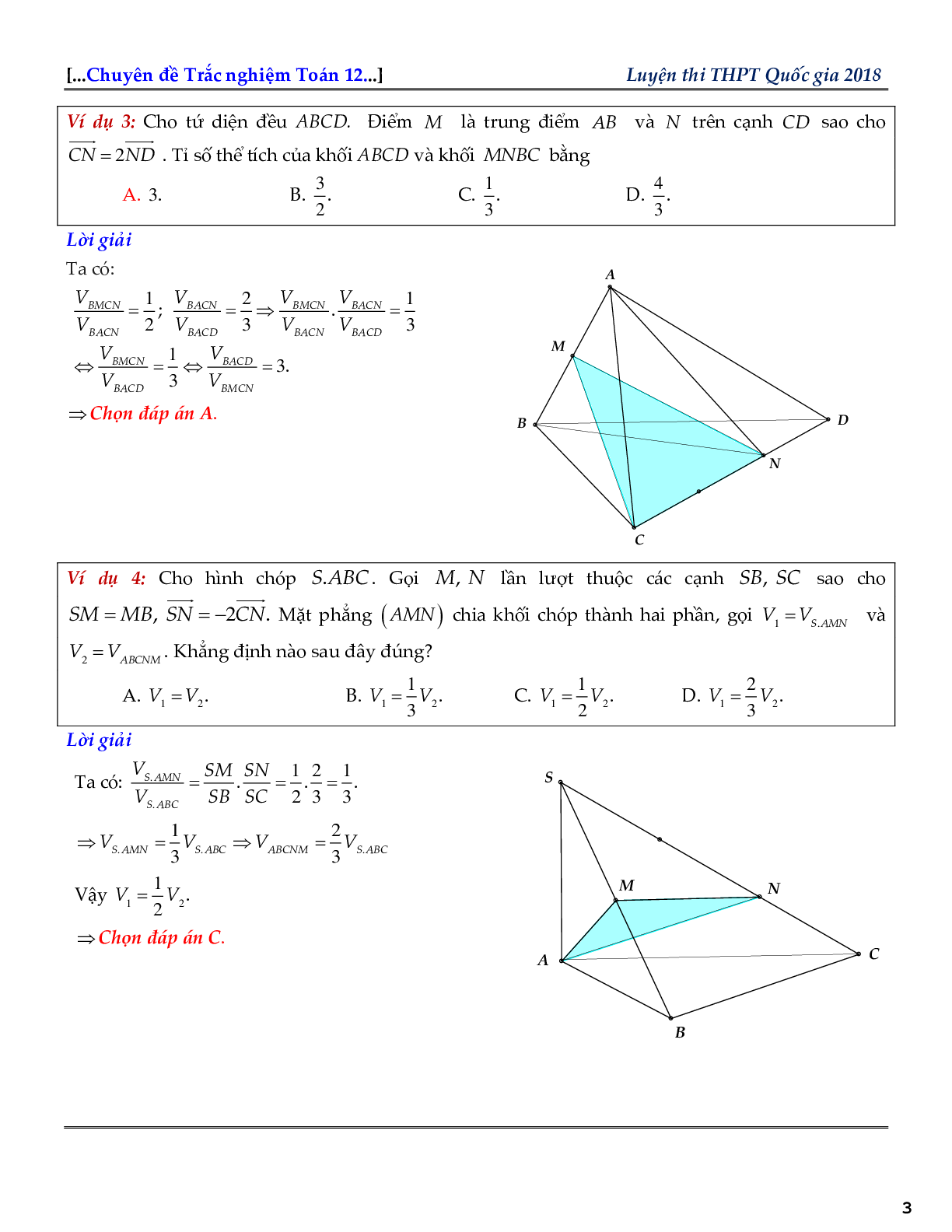
Ví dụ 3: Cho tứ diện đều ABCD. Điểm M là trung điểm AB và N trên cạnh CD sao cho \(\overrightarrow {CN}  = 2\overrightarrow {ND} \). Tỉ số thể tích của khối ABCD và khối MNBC bằng

A. 3 .

B. \(\frac{3}{2}\).

C. \(\frac{1}{3}\).

D. \(\frac{4}{3}\).

Lời giải

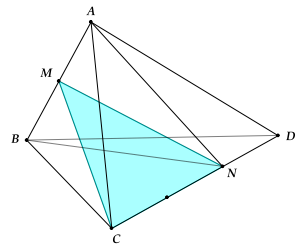
Ta có:

\(\frac{{{V_{BMCN}}}}{{{V_{BACN}}}} = \frac{1}{2};\frac{{{V_{BACN}}}}{{{V_{BACD}}}} = \frac{2}{3} \Rightarrow \frac{{{V_{BMCN}}}}{{{V_{BACN}}}} \cdot \frac{{{V_{BACN}}}}{{{V_{BACD}}}} = \frac{1}{3}\)

\( \Leftrightarrow \frac{{{V_{BMCN}}}}{{{V_{BACD}}}} = \frac{1}{3} \Leftrightarrow \frac{{{V_{BACD}}}}{{{V_{BMCN}}}} = 3.\)

\( \Rightarrow \) Chọ đáp án A.

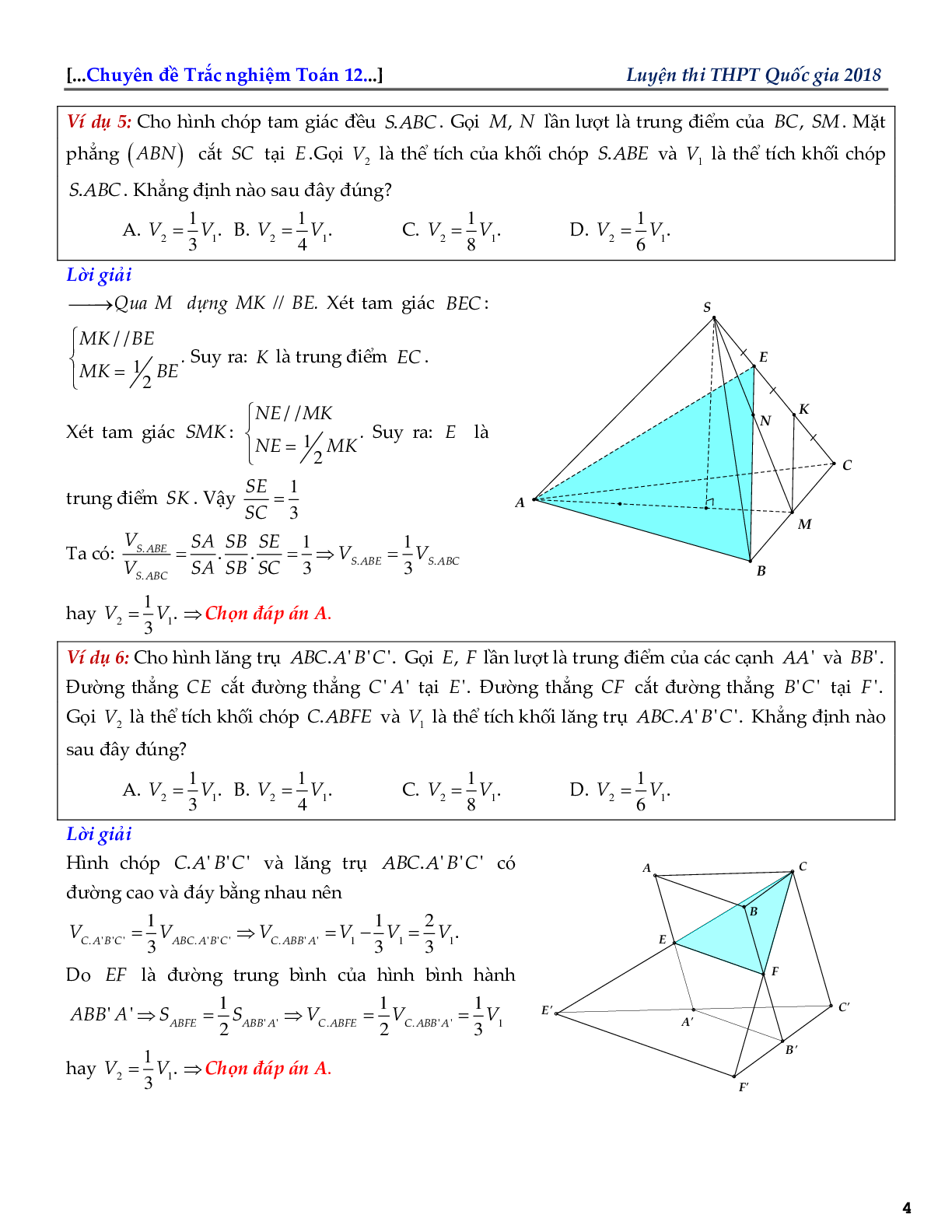
Ví dụ 4: Cho hình chóp S.ABC. Gọi M, N lần lượt thuộc các cạnh SB, SC sao cho \(SM = MB,\overrightarrow {SN}  =  - 2\overrightarrow {CN} \). Mặt phẳng (AMN) chia khối chóp thành hai phân, gọi \({V_1} = {V_{S.AMN}}\) và \({V_2} = {V_{ABCNM}}\). Khẳng định nào sau đây đúng?

A. \({V_1} = {V_2}\)

B. \({V_1} = \frac{1}{3}{V_2}\).

C. \({V_1} = \frac{1}{2}{V_2}\).

D. \({V_1} = \frac{2}{3}{V_2}\).

Lời giải

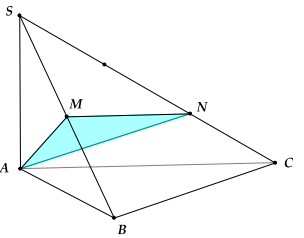
Ta có: \(\frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SB}} \cdot \frac{{SN}}{{SC}} = \frac{1}{2} \cdot \frac{2}{3} = \frac{1}{3}\).

\( \Rightarrow {V_{S.AMN}} = \frac{1}{3}{V_{S.ABC}} \Rightarrow {V_{ABCNM}} = \frac{2}{3}{V_{S.ABC}}\)

Vậy \({V_1} = \frac{1}{2}{V_2}\).

\( \Rightarrow \) Chọn đáp án \(C\).

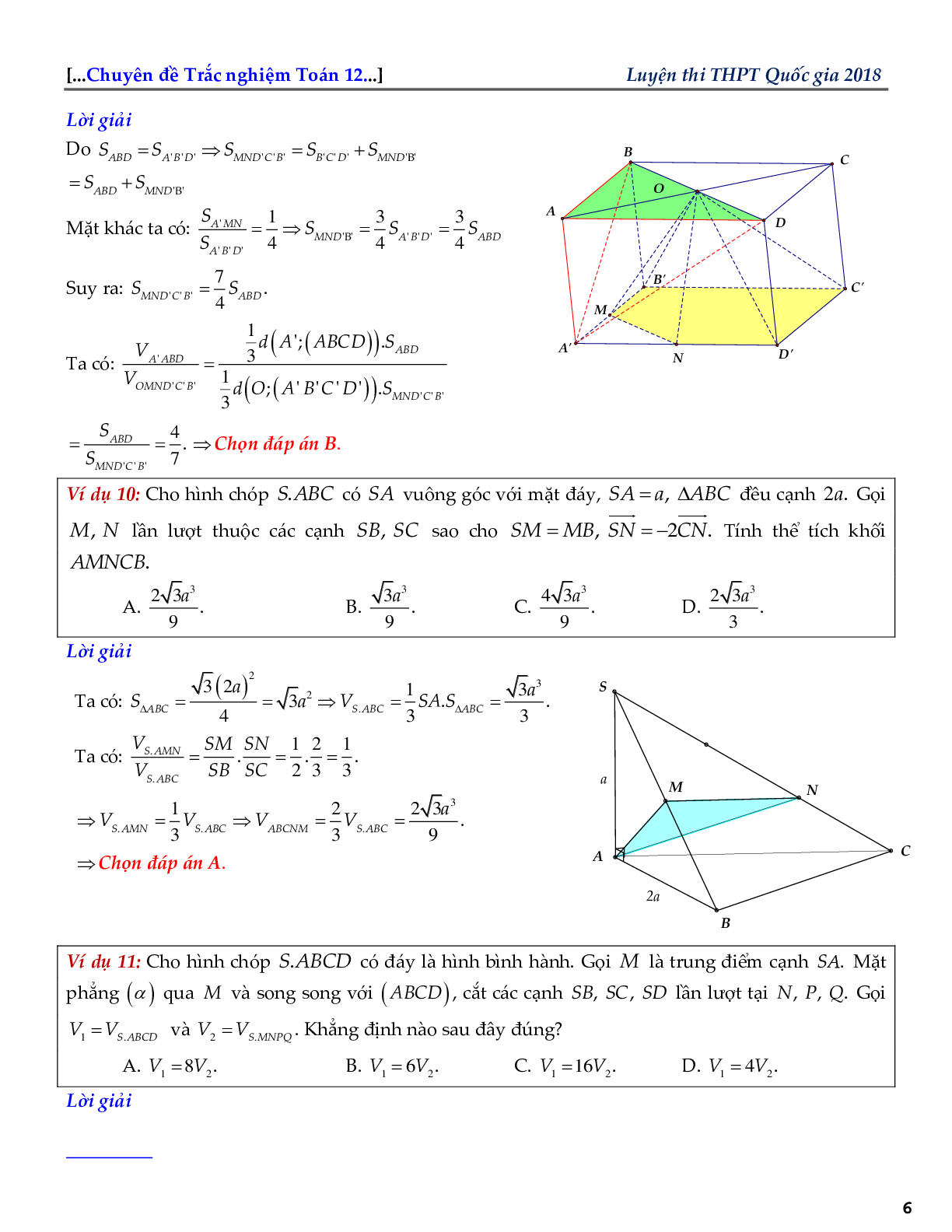
Ví dụ 5: Cho hình chóp tam giác đều S.ABC. Gọi M, N lần lượt là trung điểm của BC, SM. Mặt phẳng (ABN) cắt SC tại E.Gọi \({V_2}\) là thể tích của khối chóp S.ABE và \({V_1}\) là thể tích khối chóp S.ABC. Khẳng định nào sau đây đúng?

A. \({V_2} = \frac{1}{3}{V_1}.\)

B. \({V_2} = \frac{1}{4}{V_1}\).

C. \({V_2} = \frac{1}{8}{V_1}\).

D. \({V_2} = \frac{1}{6}{V_1}\).

Lời giải

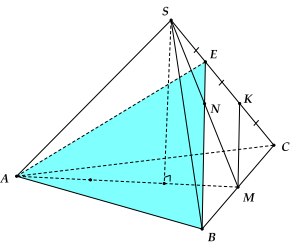
\( \to \) Qua M dụng \(MK//BE\). Xét tam giác BEC: \(\left\{ {\begin{array}{*{20}{l}}{MK//BE}\\{MK = 1/2BE}\end{array}.} \right.\)

Suy ra: K là trung điểm EC.

Xét tam giác \(SMK:\left\{ {\begin{array}{*{20}{l}}{NE//MK}\\{NE = 1/2MK}\end{array}} \right.\)

Suy ra: E là trung điểm SK. Vậy \(\frac{{SE}}{{SC}} = \frac{1}{3}\)

Ta có:

\(\begin{array}{l}\frac{{{V_{S.ABE}}}}{{{V_{S.ABC}}}} = \frac{{SA}}{{SA}} \cdot \frac{{SB}}{{SB}},\frac{{SE}}{{SC}} = \frac{1}{3}\\ \Rightarrow {V_{S.ABE}} = \frac{1}{3}{V_{S.ABC}}\end{array}\)

hay \({V_2} = \frac{1}{3}{V_1}. \Rightarrow \) Chọn đáp án A.

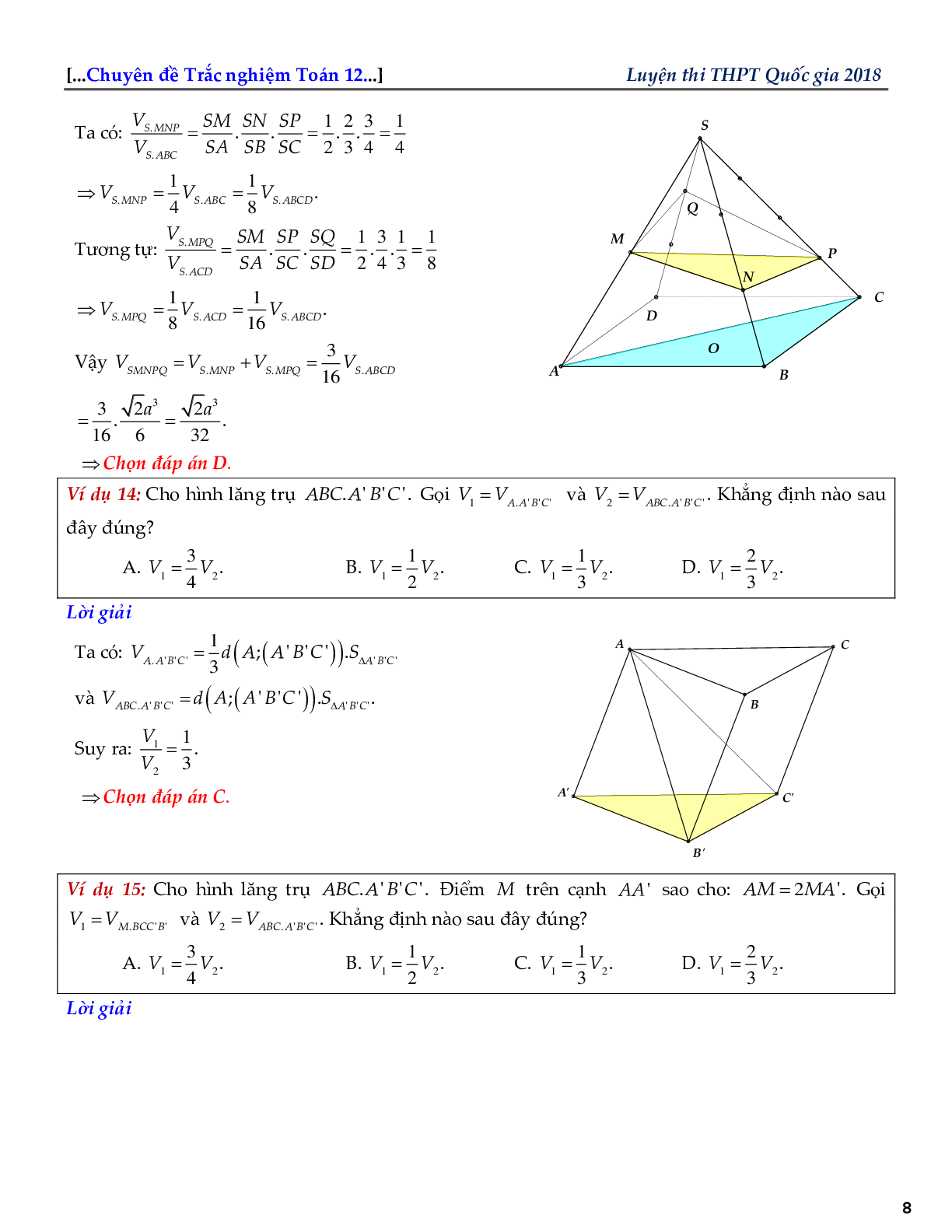
Ví dụ 6: Cho hình lăng trụ ABC. \({A^\prime }{B^\prime }{C^\prime }\). Gọi E, F lần lượt là trung điểm của các cạnh \(A{A^\prime }\) và \(B{B^\prime }\). Đường thẳng CE cắt đường thẳng \({C^\prime }{A^\prime }\) tại \({E^\prime }\). Đường thẳng CF cắt đường thẳng \({B^\prime }{C^\prime }\) tại \({F^\prime }\). Gọi \({V_2}\) là thể tích khối chóp C.ABFE và \({V_1}\) là thể tích khối lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\). Khẳng định nào sau đây đúng?

A. \({V_2} = \frac{1}{3}{V_1}.\)

B. \({V_2} = \frac{1}{4}{V_1}\).

C. \({V_2} = \frac{1}{8}{V_1}\).

D. \({V_2} = \frac{1}{6}{V_1}\).

Lời giải

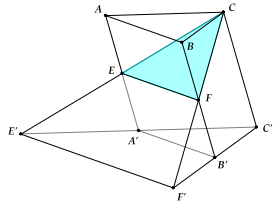
Hình chóp \(C.{A^\prime }{B^\prime }{C^\prime }\) và lăng trụ \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có đường cao và đáy bằng nhau nên

\({V_{C \cdot {A^\prime }{B^\prime }{C^\prime }}} = \frac{1}{3}{V_{ABC \cdot {A^\prime }{B^\prime }{C^\prime }}} \Rightarrow {V_{C.AB{B^\prime }{A^\prime }}} = {V_1} - \frac{1}{3}{V_1} = \frac{2}{3}{V_1}.\)

Do EF là đường trung bình của hình bình hành

Ví dụ 7: Cho hình chóp S. ABC, trên AB, BC, SC lần lượt lấy các điểm M,N,P sao cho \(AM = 2MB\), \(BN = 4NC,SP = PC\). Tỉ lệ thể tích hai khối chóp S.BMN và A.CPN là:

A. \(\frac{4}{3}\).

B. \(\frac{5}{6}\).

C. \(\frac{8}{3}\).

D. 1 .

Lời giải

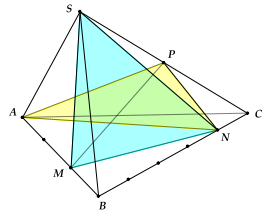
\[\begin{array}{l} + \frac{{{V_{S.BMN}}}}{{{V_{S.ABC}}}} = \frac{{{V_{B.MNS}}}}{{{V_{B.ACS}}}} = \frac{{BM}}{{BA}} \cdot \frac{{BN}}{{BC}} \cdot \frac{{BS}}{{BS}} = \frac{1}{3} \cdot \frac{4}{5} = \frac{4}{{15}}\\ + \frac{{{V_{A.CPN}}}}{{{V_{S.ABC}}}} = \frac{{{V_{C.ANP}}}}{{{V_{C.ABS}}}} = \frac{{CA}}{{CA}} \cdot \frac{{CN}}{{CB}} \cdot \frac{{CP}}{{CS}} = \frac{1}{5} \cdot \frac{1}{2} = \frac{1}{{10}}\\ \Rightarrow \frac{{{V_{S.BMN}}}}{{{V_{A.CNP}}}} = \frac{4}{{15}}:\frac{1}{{10}} = \frac{8}{3}\end{array}\]

\( \Rightarrow \) Chọn đáp án \(C\).

Ví dụ 8: (Đề minh họa Bộ GD\&ĐT) Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; \(AB = 6a,AC = 7a\) và \(AD = 4a\). Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP.

A. \(V = \frac{7}{2}{a^3}\).

B. \(V = 14{a^3}\).

C. \(V = \frac{{28}}{3}{a^3}\).

D. \(V = 7{a^3}\).

Lời giải

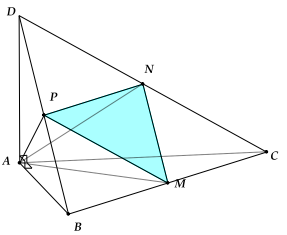
Ta có: \({V_{ABCD}} = \frac{1}{6}AB \cdot AC \cdot AD = 28{a^3}\).

Dễ thấy  được tạo nên bởi các đường trung bình của \(\Delta BCD \Rightarrow \) chúng đồng dạng với nhau theo tỉ số

\(\begin{array}{l}\frac{1}{2} \Rightarrow \frac{{{V_{AMNP}}}}{{{V_{ABCD}}}} = \frac{{{S_{MNP}}}}{{{S_{BCD}}}} = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}\\ \Rightarrow {V_{AMNP}} = \frac{1}{4}{V_{ABCD}} = 7{a^3}{\rm{. }}\end{array}\)

\( \Rightarrow \) Chọn đáp án D.

Ví dụ 9: Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Gọi O là tâm của ABCD ; M, N lần lượt là trung điểm của \({A^\prime }{B^\prime }\) và \({A^\prime }{D^\prime }\). Tỉ số thể tích của khối \({A^\prime }ABD\) và khối \(OMN{D^\prime }{C^\prime }{B^\prime }\) bằng

A. \(\frac{4}{9}\).

B. \(\frac{4}{7}\).

C. \(\frac{5}{7}\).

D. \(\frac{3}{7}\).