Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập về khối đa diện và thể tích của chúng, tài liệu bao gồm 68 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập về khối đa diện và thể tích của chúng

Chủ đề 5. Khối đa diện

Bài 1 Khái niệm về khối đa diện

I - Khối lăng trụ và khôi chóp

Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ.

Khôi chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp.

Khôi chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt.

II - Khái niệm vê hinh đa diện vả khôi đa diện

1. Khái niệm về hình đa diện

Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:

- Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.

- Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Mỗi đa giác như trên được gọi là một mặt của hình đa diện.

Các đỉnh, các cạnh của đa giác theo thứ tự gọi là các đỉnh, các cạnh của hình đa diện.

2. Khái niệm về khối đa diện

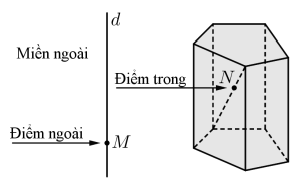
Khôi đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.

Những điểm không thuộc khố đa diện được gọi là điểm ngoài của khối đa diện. Tập hợp các điểm ngoài được gọi là miền ngoài của khô̂i đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện ứng với đa diện ấy được gọi là điểm trong của khối đa diện. Tập hợp các điểm trong được gọi là miền trong của khối đa diện.

Mỗi khối đa diện được xác định bởi một hình đa diện ứng với nó. Ta cũng gọi đỉnh, cạnh, mặt, điểm trong, điểm ngoài... của một khối đa diện theo thứ tự là đỉnh, cạnh, mặt, diểm trong, điểm ngoài... của hình đa diện tương ứng.

Ví dụ

- Các hình dưới đây là những khôî đa diện:

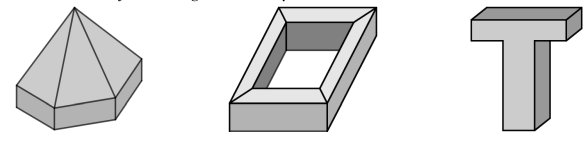
- Các hình dưới đây không phải là những khối đa diện

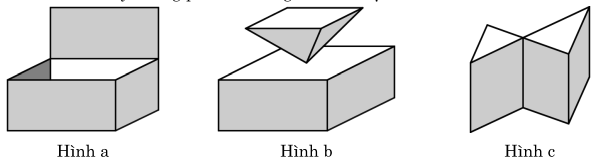
Giải thích: Hình a không phải là hình đa diện vì tồn tại cạnh không phải là cạnh chung của hai mặt, Hình b không phải là hình đa diện vì có 1 điểm đặc biệt trong hình, điểm đó không phải là đỉnh chung của hai đa giác, Hình c không phải là hình đa diện vì tồn tại 1 cạnh là cạnh chung của bốn đa giác.

Nếu khối đa diện \((\mathcal{H})\) là hợp của hai khối đa diện \(\left( {{\mathcal{H}_1}} \right)\) và \(\left( {{\mathcal{H}_2}} \right)\) sao cho \(\left( {{\mathcal{H}_1}} \right)\) và \(\left( {{\mathcal{H}_2}} \right)\) không có chung điểm trong nào thì ta nói có thể phân chia được khối đa diện \((\mathcal{H})\) thành hai khối đa diện \(\left( {{\mathcal{H}_1}} \right)\) và \(\left( {{\mathcal{H}_2}} \right)\). Khi đó ta cũng nói có thể ghép hai khôi đa diện \(\left( {{\mathcal{H}_1}} \right)\) và \(\left( {{\mathcal{H}_2}} \right)\) để được khối đa diện \((\mathcal{H})\).

Ví dụ 1. Với khôi chóp tứ giác S.ABCD, xét hai khôi chóp tam giác S .A B C và S.ACD. Ta thấy rằng:

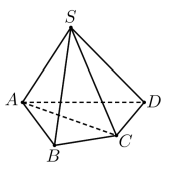
- Hai khối chóp S.ABC  và S.ACD không có điểm trong chung (tức là không tồn tại điểm trong của khối chóp này là điểm trong của khối chóp kia và ngược lại).

- Hợp của hai khối chóp S .A B C và S.ACD chính là khôi chóp S.ABCD.

Vậy khối chóp S.ABCD được phân chia thành hai khối chóp S.ABC và S,ACD hay hai khối chop Ss.abc VÀ S.ACD được ghép lại thành khối chóp S.ABCD.

Ví dụ 2. Cắt khối lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) bởi mặt phẳng \(\left( {{A^\prime }BC} \right)\). Khi đó, khối lăng trụ được phân chia thành hai khối đa diện \({A^\prime }ABC\) và \({A^\prime }BC{C^\prime }{B^\prime }\).

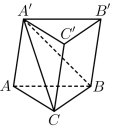
Nếu ta cắt khối chóp \({A^\prime }BC{C^\prime }{B^\prime }\) bởi mặt phẳng \(\left( {{A^\prime }{B^\prime }C} \right)\) thì ta chia khối chóp \({A^\prime }BC{C^\prime }{B^\prime }\) thành hai khối chóp \({A^\prime }BC{B^\prime }\) và \({A^\prime }C{C^\prime }{B^\prime }\).

Vậy khối lăng trụ đã cho được chia thành ba khô̂i tứ diện \({A^\prime }ABC,{A^\prime }BC{B^\prime }\) và \({A^\prime }C{C^\prime }{B^\prime }\).

Dạng 1. Nhận biết hình đa diện

Câu 1. Cho các hình sau

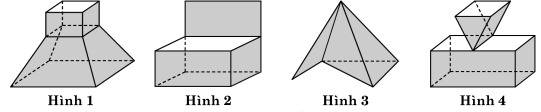
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là

A. Hình 1 .

B. Hình 2 .

C. Hình 3 .

D. Hình 4 .

Lời giải. Chọn A

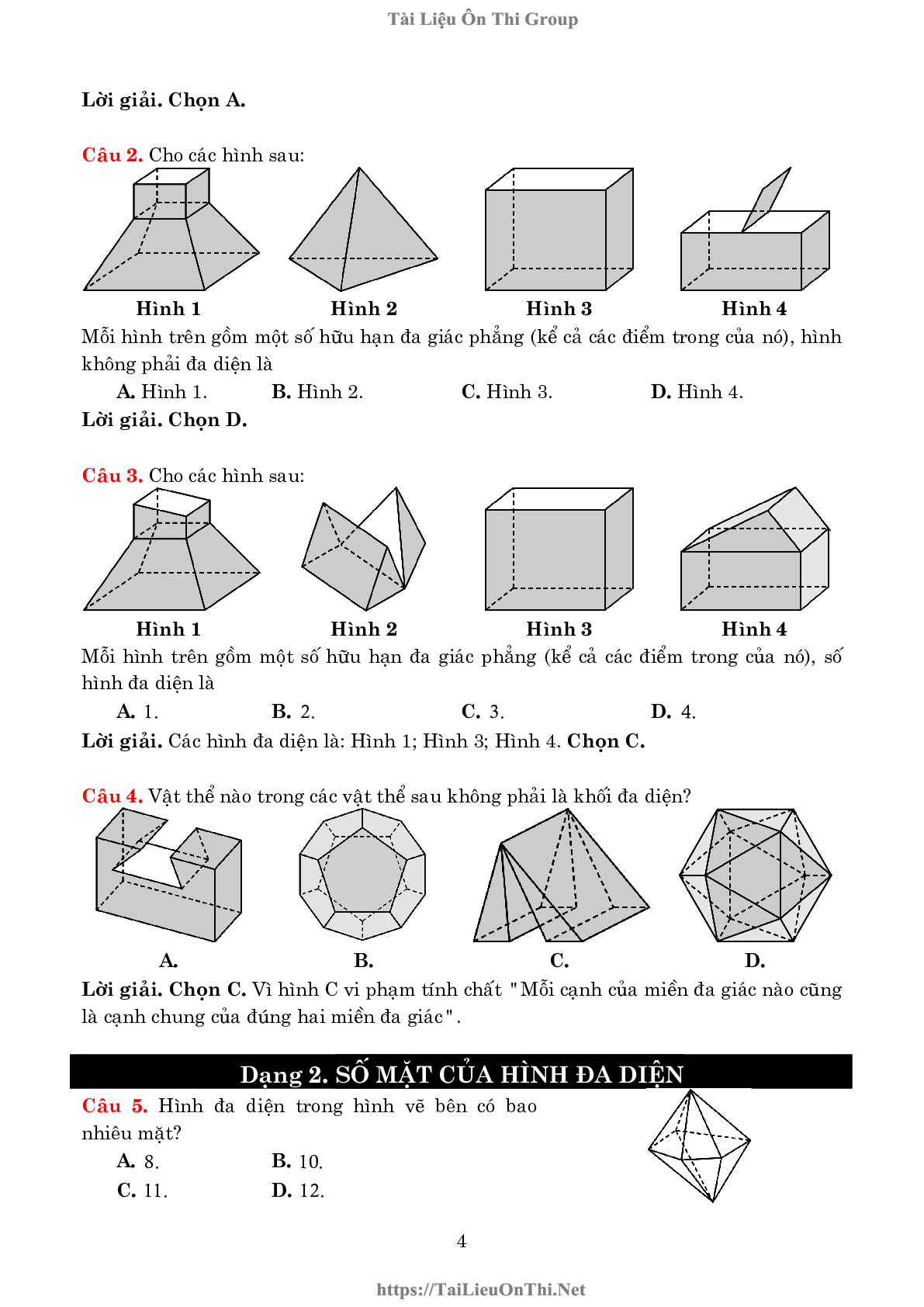
Câu 2. Cho các hình sau:

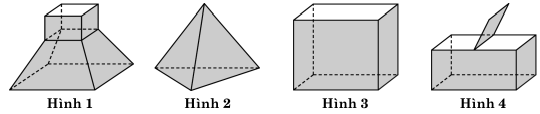
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là

A. Hình 1 .

B. Hình 2 .

C. Hình 3 .

D. Hình 4 .

Lời giải. Chọn D.

Câu 3. Cho các hình sau:

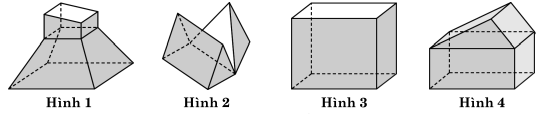
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là

A. 1 .

B. 2 .

C. 3 .

D. 4 .

Lời giải. Các hình đa diện là: Hình 1; Hình 3; Hình 4. Chọn C.

Câu 4. Vật thể nào trong các vật thể sau không phải là khô̂i đa diện?

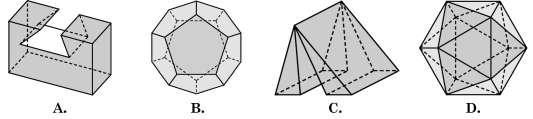
Lời giải. Chọn C. Vì hình  C vi phạm tính chất "Mỗi cạnh của miền đa giác nào cũng là cạnh chung của đúng hai miền đa giác".

Dạng 2. Số mặt của hình đa diện

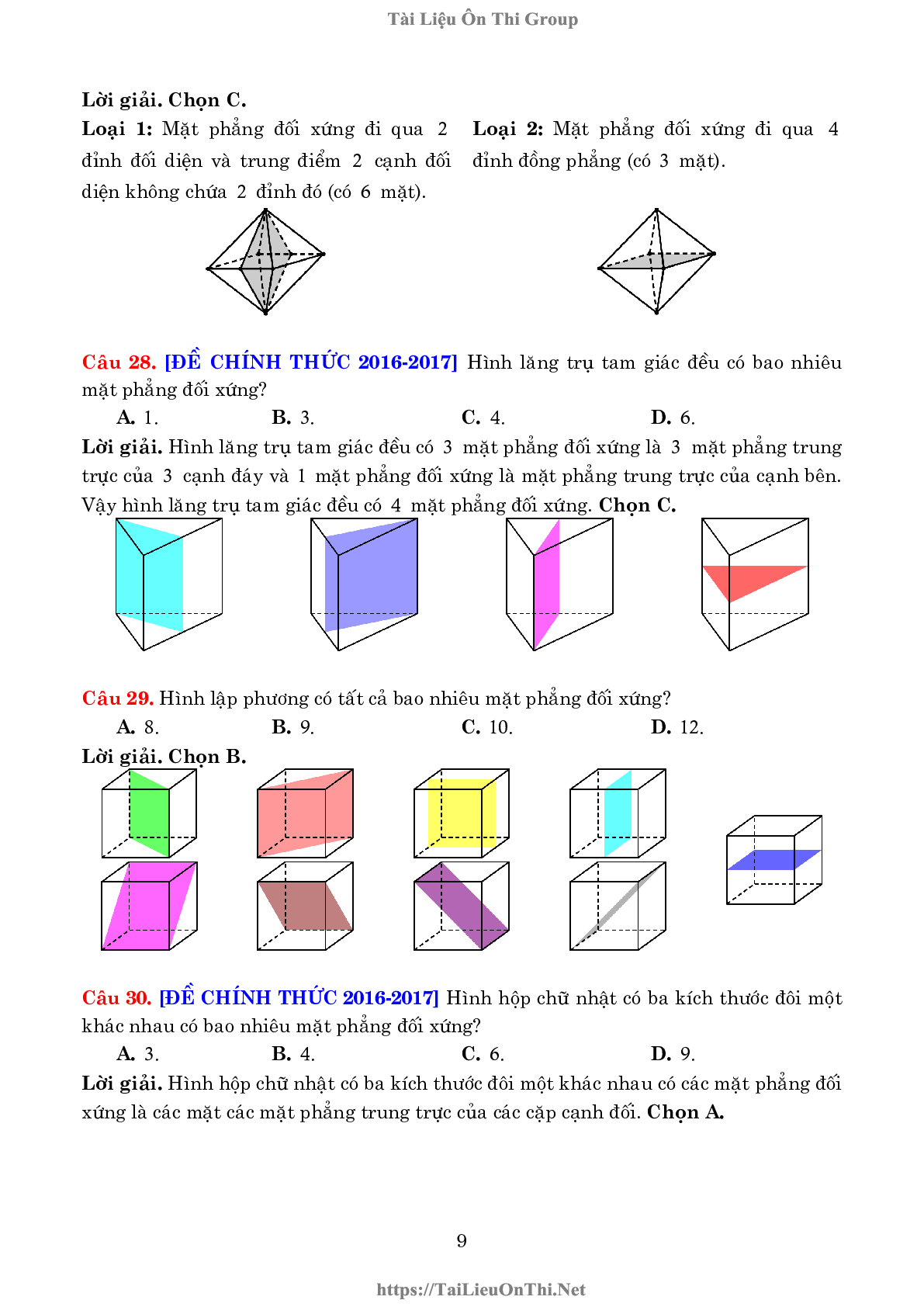
Câu 5. Hình đa diện trong hình vẽ bên có bao nhiêu mạt?

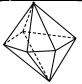
A. 8 .

B. 10 .

C. 11 .

D. 12 .

Lời giải. Chọn B.

Câu 6. Hình đa diện trong hình vẽ bên có bao nhiêu mặt?

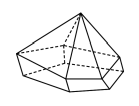
A. 6 .

B. 10 .

C. 11 .

D. 12 .

Lời giải. Chọn C.

Câu 7. Hình đa diện trong hình vẽ bên có bao nhiêu mặt?

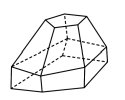
A. 11 .

B. 12 .

C. 13 .

D. 14 .

Lời giải. Chọn B.

Câu 8. Khối đa diện nào sau đây có số mặt nhỏ nhất?

A. Khối tứ diện đều.

B. Khối chóp tứ giác.

C. Khối lập phương.

D. Khô̂i 12 mặt đều.

Lời giải. Chọn A.

Câu 9. Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào sau đây đúng?

A. \(S = \sqrt 3 {a^2}\).

B. \(S = 2\sqrt 3 {a^2}\).

C. \(S = 4\sqrt 3 {a^2}\).

D. \(S = 8{a^2}\).

Lời giải. Hình bát diện đều là hình có tám mặt bằng nhau và mỗi mặt là một tam giác đều. Vậy diện tích cần tính \(S = 8 \times \frac{{{a^2}\sqrt 3 }}{4} = 2\sqrt 3 {a^2}\). Chọn B.

Dạng 3. Số cạnh của hình đa diện

Câu 10. Tính tổng độ dài \(\ell \) của tất cả các cạnh của một tứ diện đều cạnh \(a\).

A. \(\ell  = 4\).

B. \(\ell  = 4a\).

C. \(\ell  = 6\).

D. \(\ell  = 6a\).

Lời giải. Tứ diện đều có tất cả 6 cạnh nên có tổng độ dài các cạnh là 6 a. Chọn D.

Câu 11. Số cạnh của hình bát diện đều là

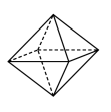
A. 12 .

B. 16 .

C. 20 .

D. 22 .

Lời giải : Chọn A