Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển chọn 30 câu số phức Vận dụng cao ôn thi THPTQG năm 2021, tài liệu bao gồm 26 trang, 30 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tuyển chọn 30 câu số phức Vận dụng cao ôn thi THPTQG năm 2021 - có lời giải chi tiết

Tinh hoa dạng toán số phức 2020 – phần 1

Câu 1 Cho \({z_1},{z_2}\)là hai trong các số phức z thỏa mãn điều kiện \(|z - 5 - 3i| = 5\), đồng thời \(\left| {{z_1} - {z_2}} \right| = 8\) Tập hợp các điểm biểu diễn của số phức \(w = {z_1} + {z_2}\) trong mặt phẳng tọa độ Oxy là đường tròn có phương trình

A. \({(x - 10)^2} + {(y - 6)^2} = 36\).

B. \({(x - 10)^2} + {(y - 6)^2} = 16\).

C. \({\left( {x - \frac{5}{2}} \right)^2} + {\left( {y - \frac{3}{2}} \right)^2} = 9\).

D. \({\left( {x - \frac{5}{2}} \right)^2} + {\left( {y - \frac{3}{2}} \right)^2} = \frac{9}{4}\).

Câu 2: Cho số phức z thỏa mãn z không phải là số thực và \(w = \frac{z}{{2 + {z^2}}}\) là số thực. Giá trị lớn nhất của biểu thức \(M = |z + 1 - i|\) là

A. 2 .

B. \(2\sqrt 2 \).

C. \(\sqrt 2 \).

D. 8 .

Câu 3: Cho số phức z thỏa mãn \(|z + 1 - i| + |z - 3 + i| = 6\). Tìm giá trị lớn nhất của \(P = |z - 4 + 4i|\).

A. \(\sqrt {53} \).

B. \( \approx 7,8\).

C. \(2\sqrt {265} \).

D. \( \approx 8,8\).

Câu 4. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của \(P = \left| {\frac{{2z + i}}{z}} \right|\), với z là số phức khác 0 và thỏa mãn \(|z| \ge 2\). Tính tỷ số \(\frac{M}{m}\).

A. \(\frac{M}{m} = 3\).

B. \(\frac{M}{m} = \frac{4}{3}\).

C. \(\frac{M}{m} = 2\).

D. \(\frac{M}{m} = \frac{5}{3}\).

Câu 5. Cho số phức z thỏa mãn \(|z + \bar z| + |z - \bar z| = 4\). Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của \(P = |z - 2 - 2i|\). Đặt A = M + m. Mệnh đề nào sau đây là đúng?

A. \(A \in [4;3\sqrt 3 )\).

B. \(A \in (\sqrt {34} ;6)\).

C. \(A \in (2\sqrt 7 ;\sqrt {33} )\).

D. \(A \in (6;\sqrt {42} )\).

Câu 6. Tìm tập hợp tất cả các giá trị của tham số m để có đúng 4 số phức z thỏa mãn đồng thời các điều kiện \(|z + \bar z| + |z - \bar z| = \left| {{z^2}} \right|\) và \(|z| = m\).

A. \(\{ 2;2\sqrt 2 \} \).

B. \([2;2\sqrt 2 ]\).

C. \(\{ 2\} \).

D. \((2;2\sqrt 2 )\).

Câu 7. Cho số phức z có \(|z| = \frac{1}{2}\) và số phức w thỏa mãn \(\frac{1}{z} + \frac{1}{w} = \frac{1}{{z + w}}\). Tính mô đun của số phức w.

A. 3 .

B. 2 .

C. \(\frac{1}{2}\).

D. \(\frac{1}{3}\).

Câu 8. Biết số phức \(z =  - \frac{a}{c} - \frac{b}{c}i\) (với a, b, c là những số tự nhiên khác 0 và \(\frac{a}{c},\frac{b}{c}\) là các phân số tối giản) thỏa mãn \(\frac{{iz - (1 + 3i)\bar z}}{{1 + i}} = |z{|^2}\). Khi đó giá trị của a là:

A. 26 .

B. 9 .

C. 90 .

D. 45 .

Câu 9. Cho số phức z thoả mãn \(|z - 1 - i| + |z - 3 - 2i| = \sqrt 5 \). Giá trị lớn nhất của \(|z + 2i|\) bằng

A. 10 .

B. 5 .

C. \(\sqrt {10} \).

D. \(2\sqrt {10} \).

Câu 10. Cho hai số phức z, w thay đổi thỏa mãn \(|z| = 3,|z - w| = 1\). Biết tập hợp điểm biểu diễn của số phức w là hình phẳng H. Tính diện tích S của hình H.

A. \(S = 20\pi \).

B. \(S = 12\pi \).

C. \(S = 4\pi \).

D. \(S = 16\pi \).

Câu 11. Có bao nhiêu số số thực a, biết rằng phương trình \({z^4} + a{z^2} + 1 = 0\) có bốn nghiệm \({z_1},\quad {z_2}\), \({z_3},{z_4}\) thỏa mãn \(\left( {z_1^2 + 4} \right)\left( {z_2^2 + 4} \right)\left( {z_3^2 + 4} \right)\left( {z_4^2 + 4} \right) = 441\) ?

A. 4 .

B. 2 .

C. 1 .

D. 3 .

Câu 12. Cho số phức z thỏa mãn \(|z| \ge 2\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(T = \left| {\frac{{z + i}}{z}} \right|\) thì tổng M + m là:

A. 2 .

B. 4 .

C. 1 .

D. 3 .

Câu 13. Có bao nhiêu số phức z thỏa mãn \(|z - 1{|^2} + |z - \bar z|i + (z + \bar z){i^{2019}} = 1\) ?

A. 4 .

B. 2 .

C. 1 .

D. 3 .

Câu 14. Giả sử \({z_1},{z_2}\) là hai trong các số phức thỏa mãn \((z - 6)(8 + \overline {zi} )\) là số thực. Biết rằng \(\left| {{z_1} - {z_2}} \right| = 4\), giá trị nhỏ nhất của \(\left| {{z_1} + 3{z_2}} \right|\) bằng

A. \(5 - \sqrt {21} \).

B. \(20 - 4\sqrt {21} \).

C. \(20 - 4\sqrt {22} \).

D. \(5 - \sqrt {22} \).

Câu 15. Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1} - {z_2} - 9 - 12i} \right| = 3\) và \(\left| {{z_1} - 3 - 20i} \right| = 7 - \left| {{z_2}} \right|\). Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức \(P = \left| {{z_1} + 2{z_2} + 12 - 15i} \right|\). Khi đó giá trị \({M^2} - {m^2}\) bằng

A. 220 .

B. 223 .

C. 224 .

D. 225 .

Câu 16. Gọi S là tập hợp các số thực m để phương trình \({z^2} + 3z + {m^2} - 2m = 0\) có một nghiệm phức \({z_0}\) với \(\left| {{z_0}} \right| = 2\). Tổng tất cả các phần tử trong S là

A. 2 .

B. 3 .

C. 4 .

D. 6 .

Câu 17. Trong mặt phẳng Oxy, gọi (H) là phần hình phẳng chứa điểm biểu diễn số phức z thỏa mãn: \(\frac{z}{{16}}\) và \(\frac{{16}}{{\bar z}}\) đều có phần thực và phần ảo thuộc đoạn [0 ; 1]. Biết diện tích của (H) là \(S = a - b\pi \) \((a,b \in \mathbb{R})\). Tính P = a + b.

A. \(P = 224\).

B. \(P = 160\).

C. \(P = 320\).

D. \(P = 256\).

Câu 18. Gọi A, B, C lần lượt là các điểm biểu diễn cho các số phức \(z,{z^2},{z^3}(z \in \mathbb{C})\). Có bao nhiêu số phức z để  vuông.

A. 1 .

B.Vô số.

C. 2 .

D. 4 .

Câu 19. Cho ba số phức \({z_1},{z_2},{z_3}\) đôi một khác nhau thỏa mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = a\). Đặt \(S = \left| {{z_1} - {z_2}} \right|\left| {{z_2} - {z_3}} \right| + \left| {{z_2} - {z_3}} \right|\left| {{z_3} - {z_1}} \right| + \left| {{z_3} - {z_1}} \right|\left| {{z_1} - {z_2}} \right|\). Giá trị nhỏ nhất của S là

A. \({a^2}\).

B. \(4{a^2}\).

C. \(9{a^2}\).

D. \(\frac{9}{4}{a^2}\).

Câu 20. Cho số phức \(z = 1 + i\). Biết rằng tồn tại các số phức \({z_1} = a + 5i,{z_2} = b\) (trong đó \(a,b \in \mathbb{R},b > 1\) ) thỏa mãn bằng \(\sqrt 3 \left| {z - {z_1}} \right| = \sqrt 3 \left| {z - {z_2}} \right| = \left| {{z_1} - {z_2}} \right|\). Tính b - a.

A. \(b - a = 5\sqrt 3 \).

B. \(b - a = 2\sqrt 3 \).

C. \(b - a = 4\sqrt 3 \).

D. \(b - a = 3\sqrt 3 \).

Câu 21. Cho số phức \(z = a + bi(a,b \in \mathbb{R})\) và thỏa mãn \(|z - 4 - 3i| = \sqrt 5 \). Tính P = a + b khi \(|z + 1 - 3i| + |z - 1 + i|\) đạt giá trị lớn nhất.

A. \(P = 10\).

B. \(P = 4\).

C. \(P = 6\).

D. \(P = 8\).

Câu 22. Cho số phức z thỏa mãn \(|z| = 2\). Tìm giá trị nhỏ nhất của biểu thức \(P = |z - 4| + 2|z - 3 + 2i|\).

A. \(P = 4\sqrt 2 \).

B. \(P = \sqrt 2 \).

C. \(P = 2\sqrt 5 \).

D. \(P = \sqrt 3 \).

Câu 23. Cho số phức z thỏa mãn \(|4z + 3i| = |4z - 4 + 5i|\). Tìm giá trị nhỏ nhất của biểu thức \(P = |z + i| + |z - 3i|.\)

A. \(\min P = 2\sqrt 2 \).

B. \(\min P = 2\sqrt 5 \).

C. \(\min P = 5\sqrt 2 \).

D. \(\min P = \sqrt 5 \).

Câu 24. Cho số phức \(z = a + bi(a,b \in \mathbb{R})\) thoả mãn: \(|z - 4| + |z + 4| = 10\) và \(|z - 6|\) lớn nhất. Tính S = a + b.

A. \(S =  - 3\).

B. \(S =  - 5\).

C. \(S = 5\).

D. \(S = 11\).

Câu 25. Xét số phức \(z = a + bi,(a,b \in \mathbb{R},b > 0)\) thỏa mãn \(|z| = 1\). Tính \(P = 2a + 4{b^2}\) khi \(\left| {{z^3} - z + 2} \right|\) đạt giá trị lớn nhất.

A. \(P = 4\).

B. \(P = 2 - \sqrt 2 \).

C. \(P = 2\).

D. \(P = 2 + \sqrt 2 \).

Câu 26. Cho hai số phức \({z_1}\) và \({z_2}\) thoả mãn \(\left| {{z_1}} \right| = 3,\left| {{z_2}} \right| = 4,\left| {{z_1} - {z_2}} \right| = \sqrt {41} \). Xét số phức \(z = \frac{{{z_1}}}{{{z_1}}} = a + bi,(a,b \in \mathbb{R})\). Khi đó |b| bằng:

A. \(\frac{{\sqrt 3 }}{8}\).

B. \(\frac{{3\sqrt 3 }}{8}\).

C. \(\frac{{\sqrt 2 }}{4}\).

D. \(\frac{{\sqrt 5 }}{4}\).

Câu 27. Cho số phức \(z = x + yi,(x,y \in \mathbb{R})\) thỏa mãn \({z^3} = 18 + 26i\). Tính \(T = {(z - 2)^2} + {(4 - z)^2}\)

A. 4 .

B. 2 .

C. 0 .

D. 1 .

Câu 28. Cho số phức z thỏa mãn \(\bar z \cdot [(3 + 4i)|z| - 4 + 3i] - 5\sqrt 2  = 0\). Giá trị của |z| là

A. \(|z| = 2\).

B. \(|z| = \sqrt 2 \).

C. \(|z| = 2\sqrt 2 \).

D. \(|z| = 1\).

Câu 29. Cho các số phức \({z_1},{z_2},z\) thỏa mãn \(\left| {{z_1} - 4 - 5i} \right| = \left| {{z_2} - 1} \right| = 1\) và \(|\bar z + 4i| = |z - 8 + 4i|\). Tính \(\left| {{z_1} - {z_2}} \right|\) khi biểu thức \(P = \left| {z - {z_1}} \right| + \left| {z - {z_2}} \right|\) đạt giá trị nhỏ nhất.

A. \(2\sqrt 5 \).

B. \(\sqrt {41} \).

C. 8 .

D. 6 .

Câu 30. Cho ba số phức \({z_1},{z_2},{z_3}\) thỏa mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1\) và \({z_1} + {z_2} + {z_3} = 0\). Tính giá trị biểu thức \(K = z_1^2 + z_2^2 + z_3^2.\)

A. \(K = 2\).

B. \(K =  - 1\).

C. \(K = 0\).

D. \(K = 1\).

Hướng dẫn giải chi tiết

Câu 1: Cho \({z_1},{z_2}\) là hai trong các số phức z thỏa mãn điều kiện \(|z - 5 - 3i| = 5\), đồng thời \(\left| {{z_1} - {z_2}} \right| = 8\). Tập hợp các điểm biểu diễn của số phức \(w = {z_1} + {z_2}\) trong mặt phẳng tọa độ Oxy là đường tròn có phương trình

A. \({(x - 10)^2} + {(y - 6)^2} = 36\).

B. \({(x - 10)^2} + {(y - 6)^2} = 16\).

C. \({\left( {x - \frac{5}{2}} \right)^2} + {\left( {y - \frac{3}{2}} \right)^2} = 9\).

D. \({\left( {x - \frac{5}{2}} \right)^2} + {\left( {y - \frac{3}{2}} \right)^2} = \frac{9}{4}\).

Lời giải

Chọn A

\(\begin{array}{l}z = x + yi,(x,y \in \mathbb{R})|z - 5 - 3i| = 5\\ \Leftrightarrow {(x - 5)^2} + {(y - 3)^2} = 25(C).\end{array}\)

Gọi A, B là các điểm biểu diễn của \({z_1},{z_2}\). Khi đó A, B thuộc đường tròn ( C) tâm I(5;3) bán kính \(R = 5\) và \(AB = \left| {{z_1} - {z_2}} \right| = 8\).

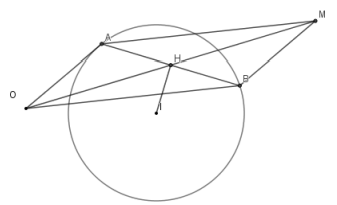
Gọi H là trung điểm của \(AB \Rightarrow IH = 3 \Rightarrow \) tập hợp H là đường tròn \(\left( {{C_1}} \right)\) tâm I(5;3) bán kính \({R_1} = 3\).

M là tập hợp các điểm biểu diễn cho số phức \(w = {z_1} + {z_2} \Rightarrow \overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OH} \).

\( \Rightarrow \) Tập hợp M là đường tròn ảnh của \(\left( {{C_1}} \right)\) qua phép vị tự tâm O(0;0) tỉ số k = 2.

\({V_{(O;2)}}\left( {{C_1}} \right) = {C^\prime } \Rightarrow {R^\prime } = 2{R_1} = 6\).

\({V_{(O;2)}}I = {I^\prime } \Rightarrow {I^\prime }(10;6)\).

\( \Rightarrow \) phương trình \({(x - 10)^2} + {(y - 6)^2} = 36\).

Câu 2: Cho số phức z thỏa mãn z không phải là số thực và \(w = \frac{z}{{2 + {z^2}}}\) là số thực. Giá trị lớn nhất của biểu thức \(M = |z + 1 - i|\) là

A. 2 .

B. \(2\sqrt 2 \).

C. \(\sqrt 2 \).

D. 8 .

Lời giải

Chọn B

Cách 1

Do \(w = \frac{z}{{2 + {z^2}}}\) là số thực \( \Rightarrow w = \bar w\)

\(\begin{array}{l} \Rightarrow \frac{z}{{2 + {z^2}}} = \frac{{\bar z}}{{2 + {{\bar z}^2}}}\\ \Leftrightarrow 2z + z.{{\bar z}^2} = 2\bar z + {z^2} \cdot \bar z\\ \Leftrightarrow 2(z - \bar z) = z.\bar z(z - \bar z)\\ \Leftrightarrow (z - \bar z)\left( {|z{|^2} - 2} \right) = 0\end{array}\)

\( \Leftrightarrow |z{|^2} = 2\) (vì \(z\) không là số thực nên \(\left. {z - \bar z \ne 0} \right) \Leftrightarrow |z| = \sqrt 2 \)

Gọi \({z^\prime } = z + 1 - i \Rightarrow |z| = \left| {{z^\prime } - 1 + i} \right| = \sqrt 2 \)

Gọi M(x,y) là điểm biểu diễn của số phức. \( \Rightarrow {(x - 1)^2} + {(y + 1)^2} = 2\)

\( \Rightarrow \) Tập hợp điểm biểu diễn số phức \({z^\prime }\) là đường tròn tâm I (1; -1), bán kính \(R = \sqrt 2 \)

Vậy \({\mathop{\rm Max}\nolimits} \left| {{z^\prime }} \right| = {\mathop{\rm Max}\nolimits} |z + 1 - i| = OI + R = 2\sqrt 2 \).

Cách 2

Do \(w = \frac{z}{{2 + {z^2}}}\) là số thực

\( \Rightarrow w = \bar w\)

\(\begin{array}{l} \Rightarrow \frac{z}{{2 + {z^2}}} = \frac{{\bar z}}{{2 + {{\bar z}^2}}} \Leftrightarrow 2z + z.{{\bar z}^2} = 2\bar z + {z^2} \cdot \bar z\\ \Leftrightarrow 2(z - \bar z) = z.\bar z(z - \bar z)\\ \Leftrightarrow (z - \bar z)\left( {|z{|^2} - 2} \right) = 0\end{array}\)

\( \Leftrightarrow |z{|^2} = 2\) (vì \(z\) không là số thực nên \(\left. {z - \bar z \ne 0} \right) \Leftrightarrow |z| = \sqrt 2 \)

Ta có \(\left| {{z^\prime } - 1 + i} \right| \le |z| + |1 - i| = \sqrt 2  + \sqrt 2  = 2\sqrt 2  \Leftrightarrow M \le 2\sqrt 2 \).

Cách 3

Gọi \(P(x;y)\) biểu diễn cho số phức \(z = x + yi\quad (x,y \in \mathbb{R})\)

Do \(z = x + yi\quad (x,y \in \mathbb{R})\) không là số thực nên \(y \ne 0\)

Do \(w = \frac{z}{{2 + {z^2}}}\) là số thực. Gọi \(\frac{z}{{2 + {z^2}}} = \frac{1}{a} \Leftrightarrow a.z = {z^2} + 2\quad (a \in \mathbb{R})\)

\(\begin{array}{l}a.z = {z^2} + 2 \Leftrightarrow a(x + yi) = {(x + yi)^2} + 2\\ \Leftrightarrow ax + ayi = {x^2} - {y^2} + 2xyi + 2\end{array}\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - {y^2} + 2 - ax = 0}\\{2xy - ay = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - {y^2} + 2 - ax = 0}\\{a = 2x}\end{array}} \right.} \right.\)

\( \Rightarrow  - {x^2} - {y^2} + 2 = 0 \Leftrightarrow {x^2} + {y^2} = 2\)

\( \Rightarrow \) Tập hợp điểm biểu diễn số phức z là đường tròn tâm O, bán kính \(R = \sqrt 2 \).

Gọi \(N = ( - 1;1)\). Ta có

\(\begin{array}{l}|z + 1 - i| = PN\\ \Rightarrow {\mathop{\rm Max}\nolimits} |z + 1 - i| = ON + R = 2\sqrt 2 \end{array}\).