Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập Vận dụng cao min - max Số phức ôn thi THPTQG môn Toán năm 2021, tài liệu bao gồm 20 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập Vận dụng cao min - max Số phức ôn thi THPTQG môn Toán năm 2021

Các dạng toán có yếu tố max- min trong số phức

A. Phân tích bài toán số phức trong đề tham khảo 2021

Ví dụ 1. (Câu 49-Đề tham khảo 2021) Xét hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 1,\left| {{z_2}} \right| = 2\)

và \(\left| {{z_1} - {z_2}} \right| = \sqrt 3 \). Giá trị lớn nhất \(\left| {3{z_1} + {z_2} - 5i} \right|\) bằng

A. \(5 - \sqrt {19} \).

B. \(5 + \sqrt {19} \).

C. \( - 5 + 2\sqrt {19} \).

D. \(5 + 2\sqrt {19} \).

Phân tích hướng giải

Đối với dạng toán có yếu tố max-min trong số phức ta có 2 hướng tiếp cận chính như sau:

+) Hướng 1: Sử dụng các phép toán số phức liên quan tới môđun để đưa bài toán về hàm số một biến rồi khảo sát hoạcc dùng các bất đẳng thức để đánh giá.

+) Hướng 2: Đưa về bài toán cực trị hình học quen thuộc

Căn cứ vào yêu câu bài toán tìm giá trị lớn nhất của biểu thức \(\left| {3{z_1} + {z_2} - 5i} \right|\) có dạng môđun của một tổng, bài toán có thể được giải quyết nếu \(\left| {3{z_1} + {z_2}} \right|\) là một hằng số, từ đó ta mạnh dạn đi tính \(\left| {3{z_1} + {z_2}} \right|\) từ các giả thiết của bài toán. Sau đó ta sẽ sử dụng một trong 2 hướng kể trên hoặc tổng hợp các hướng để kết thúc bài toán.

Lời giải tham khảo

+ Trước hết ta tính \(\left| {3{z_1} + {z_2}} \right|\) ta có một vài cách tính như sau

Cách 1: Tính toán trục tiếp

Đây là cách tiếp cận đơn giản nhất cho bài toán chỉ sử sụng những kiến thức cơ bản của số phức để biến đổi.

Đặt \({z_1} = a + bi,{z_2} = c + di\) với \(a,b,c,d \in \mathbb{R}\) và \({i^2} =  - 1\). Theo giả thiết ta suy ra

\(\begin{array}{l}\left| {{z_1}} \right| = 1 \Leftrightarrow {a^2} + {b^2} = 1\\\left| {{z_2}} \right| = 2 \Leftrightarrow {c^2} + {d^2} = 4\\\left| {{z_1} - {z_2}} \right| = \sqrt 3  \Leftrightarrow {(a - c)^2} + {(b - d)^2} = 3.\end{array}\)

Khai triển và rút gọn

\(\begin{array}{l}{a^2} - 2ac + {c^2} + {b^2} - 2bd + {d^2} = 3\\ \Rightarrow ac + bd = 1\end{array}\).

Ta có \(3{z_1} + {z_2} = (3a + c) + (3b + d)i\) nên

\(\begin{array}{l}{\left| {3{z_1} + {z_2}} \right|^2} = {(3a + c)^2} + {(3b + d)^2}\\ = 9\left( {{a^2} + {b^2}} \right) + \left( {{c^2} + {d^2}} \right) + 6(ac + bd) = 19.\end{array}\)

Suy ra \(\left| {3{z_1} + {z_2}} \right| = \sqrt {19} \).

Cách 2: Sử dụng các đẳng thúc môdun

Để sử dụng cách này đòi hỏi các em phải có kỹ năng biến đổi phép toán trên số phức ở dạng hình thức. Ta có đẳng thức

\({\left| {m{z_1} + n{z_2}} \right|^2} = {m^2}{\left| {{z_1}} \right|^2} + {m^2}{\left| {{z_2}} \right|^2} + mn\left( {{z_1}\overline {{z_2}}  + \overline {{z_1}} .{z_2}} \right).\)

Đẳng thức này ta được chứng minh nhờ hai tính chât cơ bản \(|z{|^2} = z.\bar z\) và \(\overline {{z_1} + {z_2}}  = \overline {{z_1}}  + \overline {{z_2}} \)

Thật vậy

\(\begin{array}{l}{\left| {m{z_1} + n{z_2}} \right|^2} = \left( {m{z_1} + n{z_2}} \right) \cdot \left( {\overline {m{z_1} + n{z_2}} } \right)\\ = \left( {m{z_1} + n{z_2}} \right)\left( {m{z_1} + n{z_2}} \right)n\end{array}\)

\( = {m^2}{\left| {{z_1}} \right|^2} + {m^2}{\left| {{z_2}} \right|^2} + mn\left( {{z_1}\overline {{z_2}}  + \overline {{z_1}} {z_2}} \right){\rm{ }}\)( điều phải chứng minh)

Áp dụng đẳng thức trên ta được:

\(\begin{array}{l}{\left| {3{z_1} + {z_2}} \right|^2} = 9{\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} + 3\left( {{z_1}\overline {{z_2}}  + {{\bar z}_1} \cdot {z_2}} \right)\\ = 13 + 3\left( {{z_1}\overline {{z_2}}  + {{\bar z}_1} \cdot {z_2}} \right)\end{array}\)

Lại có

\[\begin{array}{l}3 = {\left| {{z_1} - {z_2}} \right|^2} = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} - \left( {{z_1}\overline {{z_2}}  + \overline {{z_1}} .{z_2}} \right)\\ \Rightarrow \left( {{z_1}\overline {{z_2}}  + \overline {{z_1}}  \cdot {z_2}} \right) = 2\end{array}\]

Thay lại ta được \(\left| {3{z_1} + {z_2}} \right| = \sqrt {19} .\)

Cách 3: Sử dụng hình học

Để sử dụng được pháp pháp này các em cân phải vận dụng linh hoạt vê biểu diễn hình học của số phức, kết hợp với kiến thức về véctơ hay hệ thức lượng trong tam giác...để giải quyết bài toán.

Gọi A,B,C,D là các điểm biểu diênn của \({z_1},{z_2},3{z_1}, - {z_2}\) giả thiết trở thành

\[\begin{array}{l}\left| {{z_1}} \right| = 1 \Leftrightarrow OA = 1;\left| {{z_2}} \right| = 2 \Leftrightarrow OB = 2;\\\left| {{z_1} - {z_2}} \right| = \sqrt 3  \Leftrightarrow AB = \sqrt 3 \end{array}\]

Khi đó \[\left| {3{z_1} + {z_2}} \right| = CD\]

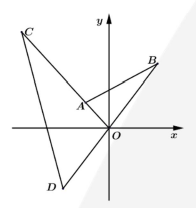
Sử dụng định lý Cosin trong tam giác \({\rm{OCD}}\) và để ý $\widehat{COD}+\widehat{AOB}={180}^{°}$ ta được

\(\begin{array}{l}C{D^2} = O{C^2} + O{D^2} - 2OC \cdot OD \cdot \cos \widehat {COD}\\ = 13 - 12\cos \widehat {COD}\\ = 13 + 12 = 13 + 12\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2OAOB}} = 19.{\rm{ }}\\{\rm{Suy ra }}\left| {3{z_1} + {z_2}} \right| = CD = \sqrt {19} \end{array}\)

Tiếp theo ta tìm giá trị lớn nhất của biểu thức \(\left| {3{z_1} + {z_2} - 5i} \right|\)

Cách 1: Sử dụng bât đẳng thúc tam giác ở dạng môdun

\( + \left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|{\rm{.}}\)Đẳng thức xảy ra khi và chỉ khi

\(\left[ {\begin{array}{*{20}{l}}{{z_2} = 0}\\{{z_2} \ne 0,\exists k \in \mathbb{R},k \ge 0:{z_1} = k{z_2}}\end{array}} \right.{\rm{. }}\)

\( + \left| {{z_1} + {z_2}} \right| \ge ||{z_1}| - |{z_2}||\).Đẳng thức xảy ra khi và chỉ khi

\({\rm{ }}\left[ {\begin{array}{*{20}{l}}{{z_2} = 0}\\{{z_2} \ne 0,\exists k \in \mathbb{R},k \le 0:{z_1} = k{z_2}}\end{array}} \right.\)

Áp dụng bất đẳng thức tam giác ở dạng moodun ta có

\(\left| {3{z_1} + {z_2} - 5i} \right| \le \left| {3{z_1} + {z_2}} \right| + | - 5i| = \sqrt {19}  + 5.\)

Dâu bằng xảy ra khi

\(3{z_1} + {z_2} = k( - 5i),k \ge 0 \Rightarrow 3{z_1} + {z_2} =  - \sqrt {19} i\).

Cách 2: Sử dụng hình học

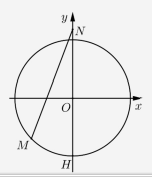
Gọi M, N lần lượt là điểm biểu diễn của \(3{z_1} + {z_2},5i\) suy ra \(OM = \sqrt {19} \) như vậy M thuộc đường tròn tâm O bán kính \(R = \sqrt {19} \) và cân tìm giá trị lớn nhất M N. Sử dụng kết quả quen thuộc ta được \(MN \le MO + ON = 5 + \sqrt {19} \).

Dấu bằng xảy ra khi M, O, N theo thứ tự thẳng hàng hay \(M(0; - \sqrt {19} )\).

Một cách tổng quát ta có thể xây dựng bài toán Max-min liên quan các yếu tố của số phức theo các dạng sau:

B. Các dạng toán thường gặp

Dạng 1: Sử dụng biến đổi đại số kết hợp với các bất đẳng thức quen thuộc để đánh giá

1.Kiến thức cần chuẩn bị:

1.1. Đẳng thức Môđun:

Cho số phức \(z = a + bi(a,b \in \mathbb{R}{\rm{ \& }}{i^2} =  - 1)\) môđun của z ký hiệu là |z| và \(|z| = \sqrt {{a^2} + {b^2}} \)

\(\begin{array}{l} + |z{|^2} = z.\bar z;\left| {{z_1} \cdot {z_2}} \right| = \left| {{z_1}} \right| \cdot \left| {{z_2}} \right|;\left| {\frac{{{z_1}}}{{{z_2}}}} \right| = \frac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}};\\|z| = |\bar z|;\left| {{z^n}} \right| = |z{|^n}(n \in \mathbb{N}*);\end{array}\)

\( + {\left| {m{z_1} + n{z_2}} \right|^2} = {m^2}{\left| {{z_1}} \right|^2} + {n^2}{\left| {{z_2}} \right|^2} + mn\left( {{z_1}{{\bar z}_2} + {{\bar z}_1}{z_2}} \right)\) với \(m,n \in \mathbb{R}\) và \({z_1},{z_2} \in \mathbb{C}\).

\( + {\left| {z + {z_1}} \right|^2} + {\left| {z + {z_2}} \right|^2} = 2\left[ {{{\left| {z + \frac{{{z_1} + {z_2}}}{2}} \right|}^2} + {{\left| {\frac{{{z_1} - {z_2}}}{2}} \right|}^2}\mid } \right.\) với \(z,{z_1},{z_2} \in \mathbb{C}.\)

\( + \left| {{z_1} + {z_2}} \right| = \left| {\frac{{\left| {{z_2}} \right|}}{{||{z_1}\mid }}{z_1} + \frac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}{z_2}} \right|\) với \({z_1},{z_2}\) là các số phức khác 0

1.2. Bất đẳng thức thường dùng

+ Bất đẳng thức tam giác ở dạng môdun

\[\left| {{z_1}} \right| + \left| {{z_2}} \right| \ge \left| {{z_1} + {z_2}} \right|\]. Đẳng thức xảy ra khi và chỉ khi

 \(\left[ {\begin{array}{*{20}{l}}{{z_2} = 0}\\{{z_2} \ne 0,\exists k \in \mathbb{R},k \ge 0:{z_1} = k{z_2}}\end{array}} \right.\).

\(\left\| {{z_1}| - |{z_2}} \right\| \le \left| {{z_1} + {z_2}} \right|\). Đẳng thức xảy ra khi và chỉ khi

 \(\left[ {\begin{array}{*{20}{l}}{{z_2} = 0}\\{{z_2} \ne 0,\exists k \in \mathbb{R},k \le 0:{z_1} = k{z_2}}\end{array}} \right.\)

 + Bất đẳng thức Bunhiacopxky \({(ax + by)^2} \le \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right)\) dấu " = "xảy ra \( \Leftrightarrow \frac{a}{b} = \frac{x}{y}.\)

Ví dụ 2. Xét các số phức \({z_1},{z_2}\) thỏa mãn \(\left| {2{z_1} + {z_2}} \right| = \sqrt {35} \) và \(\left| {3{z_1} - 2{z_2}} \right| = 7\). Giá trị lớn nhất của biểu thức \(T = \left| {{z_1}} \right| + \left| {{z_2}} \right|\) bằng

A. 4 .

B. \(\sqrt 5 \).

C. \(2\sqrt 3 \)

D. 5 .

Phân tích tìm lời giải : Tương tự như đề minh họa khi biết \(\left| {2{z_1} + {z_2}} \right| = \sqrt {35} \) và \(\left| {3{z_1} - 2{z_2}} \right| = 7\) ta có thể tính được \({m^2}{\left| {{z_1}} \right|^2} + {n^2}{\left| {{z_2}} \right|^2} = p\), đến đây dùng bất đẳng thức Bunhiacopxky là có thể đánh giá được \(T = \left| {{z_1}} \right| + \left| {{z_2}} \right|\).

Lời giải

Nhận xét \(_{z.z} = |z{|^2}\) và \(\overline {{z_1} + {z_2}}  = \overline {{z_1}}  + \overline {{z_2}} \)

\(\left\{ {\begin{array}{*{20}{l}}{35 = \left( {2{z_1} + {z_2}} \right)\left( {2\overline {{z_1}}  + \overline {{z_2}} } \right) = 4{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2} + 2\left( {{z_1}\overline {{z_2}}  + \overline {{z_1}{z_2}} } \right)}\\{49 = \left( {3{z_1} - 2{z_2}} \right)\left( {3{{\bar z}_1} - 2\overline {{z_2}} } \right) = 9{{\left| {{z_1}} \right|}^2} + 4{{\left| {{z_2}} \right|}^2} - 6\left( {{z_1}\overline {{z_2}}  + \overline {{z_1}} {z_2}} \right)}\end{array}} \right.\)

\( \Rightarrow 21{\left| {{z_1}} \right|^2} + 7{\left| {{z_2}} \right|^2} = 84 \Rightarrow 3{\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 12.\)

Ta có \(T = \frac{1}{{\sqrt 3 }} \cdot \left( {\sqrt 3 \left| {{z_1}} \right|} \right) + 1 \cdot \left( {\left| {{z_2}} \right|} \right) \le \sqrt {\left( {\frac{1}{3} + 1} \right)\left( {3{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)}  = 4\).

Đẳng thức xảy ra khi và chỉ khi \(\left\{ {\begin{array}{*{20}{l}}{\left| {{z_2}} \right| = 3\left| {{z_1}} \right|}\\{3{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2} = 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left| {{z_1}} \right| = 1}\\{{z_2}\mid  = 3}\end{array}} \right.} \right.\).

Vậy giá trị lớn nhất của T bằng 4 .