Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 7 câu trắc nghiệm Vận dụng cao - Số phức trong đề thi thử THPTQG tháng 3 năm 2021, tài liệu bao gồm 5 trang, 7 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

7 câu trắc nghiệm Vận dụng cao - Số phức trong đề thi thử THPTQG tháng 3 năm 2021 - có đáp án chi tiết

Vận dụng cao số phức trong đề thi thử THPTQG năm 2021

Tháng 3/2021

Câu 1. (THPT Quãng Xương 1-Thanh Hóa - 2021) Cho bao nhiêu số phức z thỏa mãn \(|z + 2 - i| = 2\sqrt 2 \) và \({(z - 1)^2}\) là số ảo?

A. 2 .

B. 1 .

C. 4 .

D. 3 .

Câu 2. (THPT Thanh Chương 1 - Nghệ An - 2021) Cho số phức z thỏa mãn \(|z| = 2\). Trên mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức \(w = \frac{{3 + i + z}}{{z + i}}\) là một đường tròn có bán kính bằng

A. \(2\sqrt 3 \).

B. \(2\sqrt 6 \).

C. 4 .

D. 2 .

Câu 3. (THPT Đạng Thúc Hứa - Nghệ An - 2021) Xét các số phức z thoả mãn \(|z| = 4\), biết rằng tập hợp các điểm biểu diễn của số phức \(w = (3 - 4i)z + 5i\) là một đường tròn. Bán kính r của đường tròn đó là

A. \(r = 10\).

B. \(r = 20\).

C. \(r = 18\).

D. \(r = 25\).

Câu 4. (THPT Hoàng Hoa Thám - Đà Nã̃ng - 2021) Xét các số phức z thỏa mãn \(|z + \bar z + 2| + |z - \bar z| = 6\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = |z - 3 - 2i|\). Khi đó M + m bằng

A. \(\frac{{2\sqrt {53}  + 3\sqrt 2 }}{2}\).

B. \(6\sqrt 2 \).

C. \(\frac{{2\sqrt {53}  + \sqrt 2 }}{2}\).

D. \(\sqrt {53}  + \sqrt 5 \).

Câu 5. (Chuyên KHTN - Hà Nội - 2021) Cho số phức \(z = a + bi(a,b \in \mathbb{R})\) thoả mãn \(|z - 1 + 2i| = |z - 3 - 4i|\) và \(z + 2i\bar z\) là số thực. Tổng a + b bằng

A. 1 .

B. -1.

C. 3 .

D. -3.

Câu 6. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức \({z_1},{z_2}\) là hai nghiệm của phương trình \(|2z - i| = |2 + iz|\), biết \(\left| {{z_1} - {z_2}} \right| = 1\). Giá trị của biểu thức \(P = \left| {{z_1} + {z_2}} \right|\) bằng.

A. \(\sqrt 2 \).

B. \(\frac{{\sqrt 2 }}{2}\).

C. \(\sqrt 3 \).

D. \(\frac{{\sqrt 3 }}{2}\).

Câu 7. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức \(z = a + bi\) với \(a,b \in \mathbb{R}\) thỏa mãn \(4(z - \bar z) - 15i = i{(z + \bar z - 1)^2}\) và môđun của số phức \(z - \frac{1}{2} + 3i\) đạt giá trị nhỏ nhất. Khi đó giá trị \(\frac{a}{4} + b\) bằng

A. 3 .

B. 4 .

C. 1 .

D. 2 .

Câu 1. (THPT Quãng Xương 1-Thanh Hóa - 2021) Cho bao nhiêu số phức z thỏa mãn \(|z + 2 - i| = 2\sqrt 2 \) và \({(z - 1)^2}\) là số ảo?

A. 2 .

B. 1 .

C. 4 .

D. 3 .

Chọn D

Giả sử \(z = a + bi(a,b \in \mathbb{R})\).

\(\begin{array}{l}{(z - 1)^2} = {(a + bi - 1)^2} = {[(a - 1) + bi]^2}\\ = {(a - 1)^2} - {b^2} + 2(a - 1)bi.\end{array}\)

\({(z - 1)^2}\) là số ảo khi và chỉ khi \({(a - 1)^2} - {b^2} = 0\)

\(\begin{array}{l}|z + 2 - i| = 2\sqrt 2  \Leftrightarrow |a + bi + 2 - i| = 2\sqrt 2 \\ \Leftrightarrow |(a + 2) + (b - 1)i| = 2\sqrt 2 \\ \Leftrightarrow {(a + 2)^2} + {(b - 1)^2} = 8\end{array}\)

Ta có:

\[\left\{ {\begin{array}{*{20}{l}}{{{(a - 1)}^2} = {b^2}}\\{{{(a + 2)}^2} + {{(b - 1)}^2} = 8}\end{array}} \right.\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{b = a - 1}\\{{{(a + 2)}^2} + {{(a - 2)}^2} = 8}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{b = 1 - a}\\{{{(a + 2)}^2} + {a^2} = 8}\end{array}} \right.}\end{array}} \right.\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{c}}{b = a - 1}\\{a = 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{b = 1 - a}\\{{a^2} + 2a - 2 = 0}\end{array}} \right.}\end{array}} \right.\]

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 0}\\{b =  - 1}\end{array} \vee \left\{ {\begin{array}{*{20}{l}}{a =  - 1 + \sqrt 3 }\\{b = 2 - \sqrt 3 }\end{array} \vee \left\{ {\begin{array}{*{20}{l}}{a =  - 1 - \sqrt 3 }\\{b = 2 + \sqrt 3 }\end{array}} \right.} \right.} \right.\)

Vậy có 3 số phức thỏa yêu cầu bài toán là

\(\begin{array}{l}z =  - i,z =  - 1 + \sqrt 3  + (2 - \sqrt 3 )i,\\z = z =  - 1 - \sqrt 3  + (2 + \sqrt 3 )i{\rm{. }}\end{array}\)

Câu 2. (THPT Thanh Chương  1- Nghệ An - 2021)  Cho số phức z thỏa mãn \(|z| = 2\). Trên mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức \(w = \frac{{3 + i + z}}{{z + i}}\) là một đường tròn có bán kính bằng

A. \(2\sqrt 3 \).

B. \(2\sqrt 6 \).

C. 4 .

D. 2 .

Chọn D

Lời giải

- Theo bài ra

\(\begin{array}{l}w = \frac{{3 + i + z}}{{z + i}} \Rightarrow wz + wi = 3 + i + z\\ \Rightarrow z(w - 1) = i(1 - w) + 3\end{array}\)

\( \Rightarrow |z|.|w - 1| = |i(1 - w) + 3| = |w - 1 + 3i|\).

Đặt

\(\begin{array}{l}w = a + bi \Rightarrow 2|a + bi - 1| = |(a + bi) + 3i - 1|\\ \Leftrightarrow 2|a + bi - 1| = |(b + 3)i + a - 1|\end{array}\)

\(\begin{array}{l} \Leftrightarrow 4\left[ {{{(a - 1)}^2} + {b^2}} \right] = {(a - 1)^2} + {(b + 3)^2}\\ \Leftrightarrow 3{(a - 1)^2} + 3{b^2} - 6b - 9 = 0\end{array}\)

\(\begin{array}{l} \Leftrightarrow {(a - 1)^2} + {b^2} - 2b + 1 - 4 = 0\\ \Leftrightarrow {(a - 1)^2} + {(b - 1)^2} = 4.{\rm{ }}\end{array}\)

Tập hợp điểm biểu diễn w là đường tròn bán kính \(R = 2\).

Câu 3. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Xét các số phức z thoả mãn \(|z| = 4\), biết rằng tập hợp các điểm biểu diễn của số phức \(w = (3 - 4i)z + 5i\) là một đường tròn. Bán kính \(r\) của đường tròn đó là

A. r = 10.

B. r = 20.

C. r = 18.

D. r = 25.

Lời giải

Chọn B

Gọi \(w = x + yi\) với \(x,y \in \mathbb{R}\).

Ta có \(w = (3 - 4i)z + 5i \Leftrightarrow z = \frac{{w - 5}}{{3 - 4i}}\).

Mà \(|z| = 4 \Leftrightarrow \left| {\frac{{w - 5}}{{3 - 4i}}} \right| = 4 \Leftrightarrow |w - 5| = 20\)

\( \Leftrightarrow {(x - 5)^2} + {y^2} = 400\).

Vậy tập hợp điểm biểu diễn số phức là đường tròn có bán kính r = 20.

Câu 4. (THPT Hoàng Hoa Thám - Đà Nã̃ng - 2021) Xét các số phức z thỏa mãn \(|z + \bar z + 2| + |z - \bar z| = 6\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = |z - 3 - 2i|\). Khi đó M + m bằng

A. \(\frac{{2\sqrt {53}  + 3\sqrt 2 }}{2}\).

B. \(6\sqrt 2 \).

C. \(\frac{{2\sqrt {53}  + \sqrt 2 }}{2}\).

D. \(\sqrt {53}  + \sqrt 5 \).

Chọn A

Lời giải

Gọi \(z = x + yi\) và điểm E(x;y) biểu diễn cho số phức z trong mặt phẳng tọa độ Oxy

Ta có:

\(\begin{array}{l}|z + \bar z + 2| + |z - \bar z| = 6 \Rightarrow |2x + 2| + |2yi| = 6\\ \Rightarrow 2|x + 1| + 2|y| = 6\end{array}\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{x + 1 + y = 3}\\{x + 1 - y = 3}\\{ - x - 1 + y = 3}\\{ - x - 1 - y = 3}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{x + y - 2 = 0\left( {{d_1}} \right)}\\{x - y - 2 = 0\left( {{d_2}} \right)}\\{x + y + 4 = 0\left( {{d_3}} \right)}\\{x - y + 4 = 0\left( {{d_4}} \right)}\end{array}} \right.} \right.\)

Suy ra điểm \(E\) nằm trên các cạnh của hình vuông A B C D có các cạnh nằm trên các đường thẳng \({d_1},{d_2},{d_3},{d_4}\) như hình vẽ

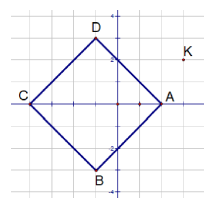
Ta có: \(P = |z - (3 + 2i)| = EK\) với \(K(3;2)\) là điểm biểu diễn cho số phức \(3 + 2i\).

\(\begin{array}{l}\min P = \min EK = d(K,AD) = \frac{3}{{\sqrt 2 }}{\rm{ }}\\{\rm{va  }}\max P = \max EK = KC = \sqrt {53} \end{array}\)

Câu 5. ( Chuyên KHTN – Hà nội - 2021) Cho số phức z=a+bi \((a,b \in R)\) thoả mãn \(|z - 1 + 2i| = |z - 3 - 4i|\) và \(z + 2i\bar z\) là số thực. Tổng a + b bằng

A. 1 .

B. -1.

C. 3 .

D. -3.

Chọn A

Lời giải

\(|z - 1 + 2i| = |z - 3 - 4i| \Leftrightarrow |a - 1 + (b + 2)i| = |a - 3 + (b - 4)i|\) \(\begin{array}{l} \Leftrightarrow {(a - 1)^2} + {(b + 2)^2} = {(a - 3)^2} + {(b - 4)^2}\\ \Leftrightarrow a + 3b = 5(1).\end{array}\)

 \(z + 2i\bar z = a + bi + 2i(a - bi) = a + 2b + (b + 2a)i.\)

\(z + 2i\bar z\) là số thực nên \(b + 2a = 0(2).\)

Từ (1) và (2) ta có hệ phương trình

 \(\left\{ {\begin{array}{*{20}{l}}{a + 3b = 5}\\{2a + b = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a =  - 1}\\{b = 2}\end{array} \Rightarrow a + b = 1.} \right.} \right.\)

Câu 6. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức \({z_1},{z_2}\) là hai nghiệm của phương trình \(|2z - i| = |2 + iz|\), biết \(\left| {{z_1} - {z_2}} \right| = 1\). Giá trị của biểu thức \(P = \left| {{z_1} + {z_2}} \right|\) bằng.

A. \(\sqrt 2 \).

B. \(\frac{{\sqrt 2 }}{2}\).

C. \(\sqrt 3 \).

D. \(\frac{{\sqrt 3 }}{2}\).

Lời giải

Chọn C

Gọi \(z = a + bi\quad (a,b \in \mathbb{R})\).

Ta có:

\(\begin{array}{l}|2z - i| = |2 + iz| \Leftrightarrow {(2a)^2} + {(2b - 1)^2} = {(2 - b)^2} + {a^2}\\ \Leftrightarrow {a^2} + {b^2} = 1.{\rm{ }}\end{array}\)

Vậy số phức \({z_1},{z_2}\) có mô đun bằng 1 .

Gọi \({z_1} = {a_1} + {b_1}i;{z_2} = {a_2} + {b_2}i\quad \left( {{a_1},{b_1},{a_2},{b_2} \in \mathbb{R},a_1^2 + b_1^2 = 1;a_2^2 + b_2^2 = 1} \right)\).

\(\begin{array}{l}\left| {{z_1} - {z_2}} \right| = 1 \Leftrightarrow {\left( {{a_1} - {a_2}} \right)^2} + {\left( {{b_1} - {b_2}} \right)^2} = 1\\ \Leftrightarrow 2{a_1}{a_2} + 2{b_1}{b_2} = 1\\P = \left| {{z_1} + {z_2}} \right| = \sqrt {{{\left( {{a_1} + {a_2}} \right)}^2} + {{\left( {{b_1} + {b_2}} \right)}^2}} \\ = \sqrt {a_1^2 + b_1^2 + a_2^2 + b_2^2 + 2{a_1}{a_2} + 2{b_1}{b_2}}  = \sqrt 3 \end{array}\)

Câu 7. ( Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức z=a+bi với \(a,b \in \mathbb{R}\) thỏa mãn \(4(z - \bar z) - 15i = i{(z + \bar z - 1)^2}\) và môđun của số phức \(z - \frac{1}{2} + 3i\) \(a + b\) bằng

A. 3 .

B. 4 .

C. 1 .

D. 2 .

Chọn D

Lời giải

Ta có:

\(\begin{array}{l}4(z - \bar z) - 15i = i{(z + \bar z - 1)^2}\\ \Rightarrow 4(a + bi - a + bi) - 15i = i{(a + bi + a - bi - 1)^2}\end{array}\)

\( \Leftrightarrow 8b - 15 = {(2a - 1)^2} \Rightarrow 8b - 15 \ge 0 \Rightarrow b \ge \frac{{15}}{8}.\)

Theo giả thiêt:

\(\begin{array}{l}\left| {z - \frac{1}{2} + 3i} \right| = \left| {\left( {a - \frac{1}{2}} \right) + (b + 3)i} \right|\\ = \sqrt {{{\left( {a - \frac{1}{2}} \right)}^2} + {{(b + 3)}^2}} \\ = \frac{1}{2}\sqrt {{{(2a - 1)}^2} + {{(2b + 6)}^2}} \\ = \frac{1}{2}\sqrt {(8b - 15) + {{(2b + 6)}^2}} \\ = \frac{1}{2}\sqrt {4{b^2} + 32b + 21} \end{array}\)

Xét hàm số \(f(b) = 4{b^2} + 32b + 21\) với \(b \ge \frac{{15}}{8}\).

Ta có \({f^\prime }(b) = 8b + 32 > 0,\forall b \ge \frac{{15}}{8}\) nên hàm số \(f(b) = 4{b^2} + 32b + 21\) đồng biến trên \(\left[ {\frac{{15}}{8}; + \infty } \right)\).

Suy ra: \(f(b) \ge f\left( {\frac{{15}}{8}} \right) = \frac{{4353}}{{16}}\).

Do đó \(\left| {z - \frac{1}{2} + 3i} \right|\) đạt giá trị nhỏ nhất là \(\frac{1}{2}\sqrt {\frac{{4353}}{{16}}} \) khi \(b = \frac{{15}}{8},a = \frac{1}{2}\).

Vậy \(\frac{a}{4} + b = \frac{{\frac{1}{2}}}{4} + \frac{{15}}{8} = 2\).