Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập về các cách giải đơn điệu Hàm số, tài liệu bao gồm 11 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Bài toán 1: Tính đơn điệu của hàm số

Bài toán 2: Tìm m để đơn điệu trên \({\rm{R}}\) và các khoảng xác định

Bài toán 3: Tìm m để hàm số đơn điệu trên 1 khoảng, nữa khoảng hoặc 1 đợn bất kỳ

Bài toán 4: Đặt ẩn phụ giải đơn điệu trên khoảng

Bài toán 5. Cho đồ thị đọc khoảng đơn

Bài tập về các cách giải đơn điệu Hàm số

Bài toán 1: Tính đơn điệu của hàm số

Phương pháp chung:

Bước 1. Tìm tập xác định \(D\) của hàm số.

Bước 2. Tính đạo hàm \({y^\prime } = {f^\prime }(x).\)

Tìm các điểm \({x_i},(i = 1,2,3, \ldots ,n)\) mà tại đó đạo hàm bằng 0 hoặc không xác định.

Bước 3 . Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên.

Bước 4 . Nêu kết luận về các khoảng đồng biến và nghịch biến dựa vào bảng biến thiên.

Nhớ công thức tính đạo hàm:

\({\left( {{u^\alpha }} \right)^\prime } = \alpha  \cdot {u^{\alpha  - 1}} \cdot {u^\prime }\)

\({\left( {\frac{u}{v}} \right)^\prime } = \frac{{{u^\prime }v - {v^\prime }u}}{{{v^2}}}\)

\({(\sqrt u )^\prime } = \frac{{{u^\prime }}}{{2\sqrt u }}\)

Xét hàm số bậc ba \(y = f(x) = a{x^3} + b{x^2} + cx + d.\)

Bước 1. Tập xác định: \(D = \mathbb{R}\).

Bước 2. Tính đạo hàm

\({y^\prime } = {f^\prime }(x) = 3a{x^2} + 2bx + c{\rm{. }}\)

+ Để f(x) đồng biến trên \(\mathbb{R} \Leftrightarrow \) \({y^\prime } = {f^\prime }(x) \ge 0,\forall x \in \mathbb{R}\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a_{{f^\prime }(x)}} = 3a > 0}\\{{\Delta _{{f^\prime }(x)}} = 4{b^2} - 12ac \le 0}\end{array} \Rightarrow m?} \right.\)

+ Để f(x) nghịch biến trên \[{\rm{ }}\mathbb{R} \Leftrightarrow {y^\prime } = {f^\prime }(x) \le 0,\forall x \in \mathbb{R}\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a_{{f^\prime }(x)}} = 3a < 0}\\{{\Delta _{{f^\prime }(x)}} = 4{b^2} - 12ac \le 0}\end{array} \Rightarrow m?} \right.\]

Xét hàm số \(y = f(x) = \frac{{ax + b}}{{cx + d}}\).

Bước 1. Tập xác định\({\rm{ }}D = \mathbb{R}\backslash \left\{ { - \frac{d}{c}} \right\}{\rm{. }}\)

Bước 2. Tính đạo hàm

\({y^\prime } = {f^\prime }(x) = \frac{{a \cdot d - b \cdot c}}{{{{(cx + d)}^2}}}\).

+ Để \(f(x)\) đồng biến trên \(D \Leftrightarrow {y^\prime } = {f^\prime }(x) > 0,\forall x \in D\)

\( \Leftrightarrow a.d - b.c > 0 \Rightarrow m\) ?

+ Để \(f(x)\) nghịch biến trên \(D \Leftrightarrow {y^\prime } = {f^\prime }(x) < 0,\forall x \in D\)

\( \Leftrightarrow a \cdot d - b.c < 0 \Rightarrow m\) ?

* Lưu ý: Đối với hàm

\(y = f(x) = \frac{{ax + b}}{{cx + d}} \cdot \) thì không có dấu " =" xày ra tại vị trí \({y^\prime }\).

Dạng: \(y = f(x,m) = \frac{{ax + b}}{{cx + d}}\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ad - bc > 0( < 0)}\\{x =  - \frac{d}{c} \notin D}\end{array}} \right.\)

Dạng : \(y = f(x,m)\) : đa thức

Bước 1. Ghi điêu kiện để \(y = f(x;m)\) đơn điệu trên \(D\). Chẳng hạn:

Đề yêu cầu \(y = f(x;m)\) đồng biến trên \(D \Leftrightarrow {y^\prime } = {f^\prime }(x;m) \ge 0.{\rm{ }}\)

Đề yêu cầu \(y = f(x;m)\) nghịch biến trên \(D \Leftrightarrow {y^\prime } = {f^\prime }(x;m) \le 0.{\rm{ }}\)

Bước 2. Độc lập m ra khỏi biến số và đặt vế còn lại là g(x) đưọc: \(\left[ {\begin{array}{*{20}{l}}{m \ge g(x)}\\{m \le g(x)}\end{array}} \right.\).

Bước 3. Khảo sát tính đơn điệu của hàm số \(g(x)\) trên \(D\).

Bước 4. Dựa vào bảng biến thiên kết luận \(\left[ {\begin{array}{*{20}{l}}{{\rm{ Khi }}m \ge g(x) \Rightarrow m \ge {{\max }_D}g(x)}\\{{\rm{ Khi }}m \le g(x) \Rightarrow m \le {{\min }_D}g(x)}\end{array}} \right.\).

-  Kiểm tra tính đồng biến,nghịch biến của hàm đổi biến ( là hàm biến cũ là biến và biến mới là hàm).

 Nếu hàm đổi biến đồng biến thì bài toán ban đầu giữ nguyên tính đơn điệu

 Hàm cũ (với biến cũ ) đồng biến chuyển về hàm mới (với biến mới) vẫn đồng biến.

 Hàm cũ (với biến cũ ) nghịch biến chuyển về hàm mới (với biến mới) vẫn nghịch biến.

 Nếu hàm đổi biến nghịch biến thì bài toán ban đầu đổi lại tính đơn điệu

 Hàm cũ (với biến cũ ) đồng biến chuyển về hàm mới (với biến mới) đổi thành nghịch biến.

 Hàm cũ (với biến cũ ) nghịch biến chuyển về hàm mới (với biến mới) đổi thành đồng biến.

Ví dụ như ở câu hỏi 29 trên do hàm đổi biến do \(t = \sin x\) nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\).Nên hàm số ban đầu \(y = \frac{{\sin x - m}}{{\sin x + m}}\) nghịch biến trên \(\left( {\frac{\pi }{2};\pi } \right)\) sẽ chuyền về hàm số mới \(y = \frac{{t - m}}{{t + m}}\) đồng biến trên \((0;1)\)

Bài tập trắc nghiệm

1. Cho hàm số \(y = {x^3} + 3x + 2\). Mệnh đề nào dưới đây là đúng?

A. Hàm số đồng biến trên khoảng \(( - \infty ;0)\) và nghịch biến trên khoảng \((0; + \infty )\).

B. Hàm số nghịch biến trên khoảng \(( - \infty ; + \infty )\).

C. Hàm số đồng biến trên khoảng \(( - \infty ; + \infty )\).

D. Hàm số nghịch biến trên khoảng \(( - \infty ;0)\) và đồng biến trên khoảng \((0; + \infty )\).

2. Hàm số \(y = \frac{2}{{{x^2} + 1}}\) nghịch biến trên khoảng nào dưới đây?

A. \((0; + \infty )\)

B. \(( - 1;1)\)

C. \(( - \infty ; + \infty )\)

D. \(( - \infty ;0)\)

3. Hàm số nào sau đây đồng biến trên khoảng \(( - \infty ; + \infty )\)

A. \(y = \frac{{x + 1}}{{x + 3}}\).

B. \(y = {x^3} + x\).

C. \(y = \frac{{x - 1}}{{x - 2}}\).

D. \(y =  - {x^3} - 3x\).

4. Cho hàm số \(y = {x^3} - 3{x^2}\). Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng (0;2)

B. Hàm số nghịch biến trên khoảng \((2; + \infty )\)

C. Hàm số đồng biến trên khoảng (0;2)

D. Hàm số nghịch biến trên khoảng \(( - \infty ;0)\)

5. Cho hàm số y = f(x) có đạo hàm \({f^\prime }(x) = {x^2} + 1,\forall x \in \mathbb{R}\). Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng \(( - \infty ;0)\).

B. Hàm số nghịch biến trên khoảng \((1; + \infty )\).

C. Hàm số nghịch biến trên khoảng \(( - 1;1)\).

D. Hàm số đồng biến trên khoảng \(( - \infty ; + \infty )\).

6. Cho hàm số \(y = {x^4} - 2{x^2}\). Mệnh đề nào dưới đây là đúng?

A. Hàm số đồng biến trên khoảng \(( - \infty ; - 2)\)

B. Hàm số nghịch biến trên khoảng \(( - \infty ; - 2)\)

C. Hàm số đồng biến trên khoảng \(( - 1;1)\)

D. Hàm số nghịch biến trên khoảng \(( - 1;1)\)

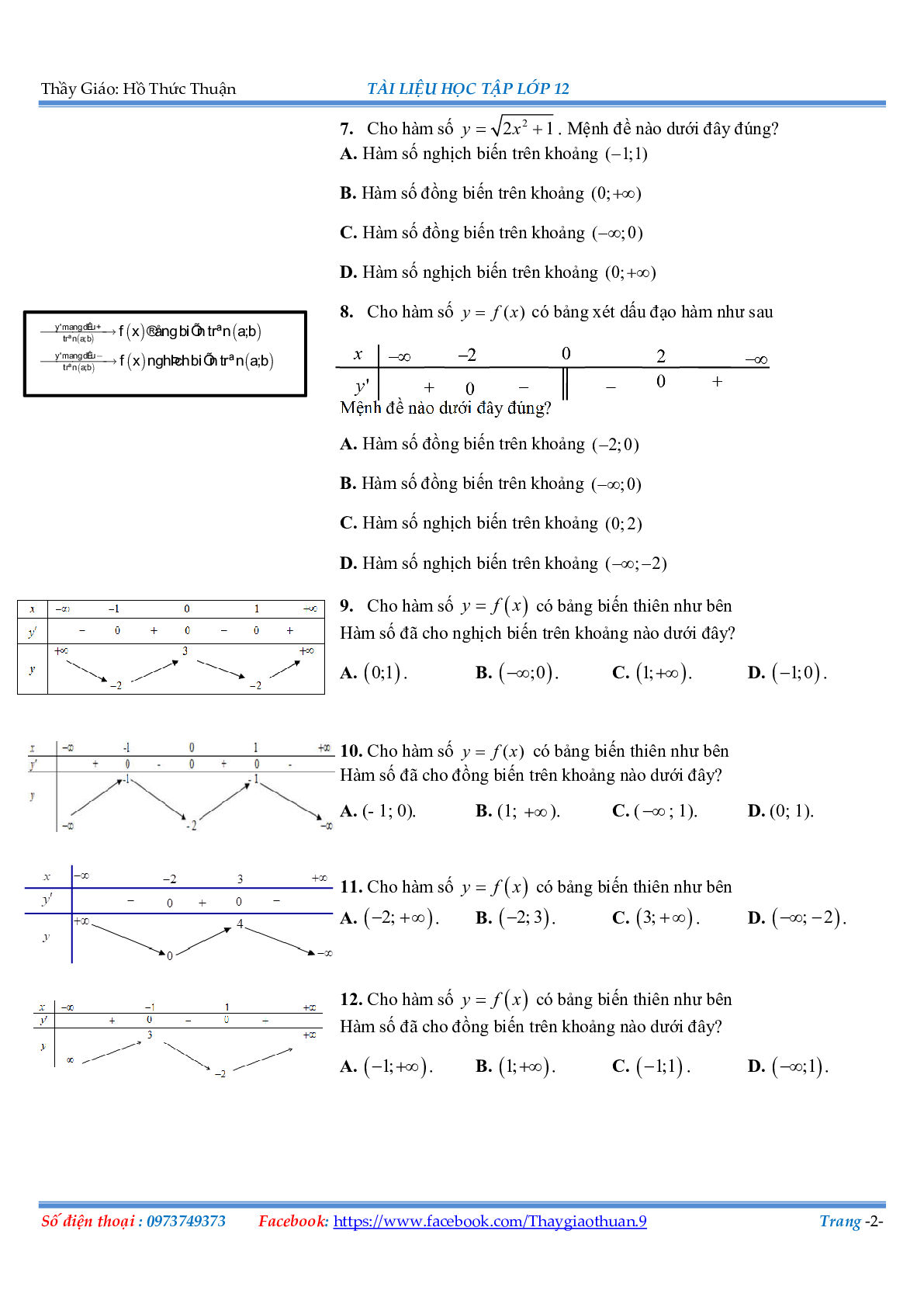
7. Cho hàm số \(y = \sqrt {2{x^2} + 1} \). Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng \(( - 1;1)\)

B. Hàm số đồng biến trên khoảng \((0; + \infty )\)

C. Hàm số đồng biến trên khoảng \(( - \infty ;0)\)

D. Hàm số nghịch biến trên khoảng \((0; + \infty )\)

8. Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng \(( - 2;0)\)

B. Hàm số đồng biến trên khoảng \(( - \infty ;0)\)

C. Hàm số nghịch biến trên khoảng \((0;2)\)

D. Hàm số nghịch biến trên khoảng \(( - \infty ; - 2)\)

9. Cho hàm số y = f(x) có bảng biến thiên như bên.

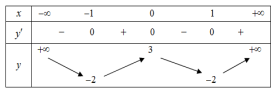
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (0;1).

B. \(( - \infty ;0)\).

C. \((1; + \infty )\).

D. (-1;0).

10. Cho hàm số y = f(x) có bảng biến thiên như bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

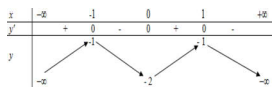
A. (-1 ; 0)

B. \((1; + \infty )\).

C. \(( - \infty ;1)\).

D. (0;1).

Câu 11, Cho hàm số y = f(x) có bảng biến thiên như bên:

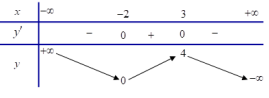
A. \(( - 2; + \infty )\).

B. \(( - 2;3)\).

C. \((3; + \infty )\).

D. \(( - \infty ; - 2)\).

Câu 12. Cho hàm số y = f(x) có bảng biến thiên như hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

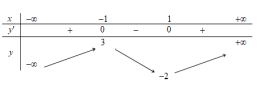
A. \(( - 1; + \infty )\).

B. \((1; + \infty )\).

C. \(( - 1;1)\).

D. \(( - \infty ;1)\).

Bài toán 2: Tìm m để đơn điệu trên \({\rm{R}}\) và các khoảng xác định

13. Cho hàm số \(y =  - {x^3} - m{x^2} + (4m + 9)x + 5\) với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng \[( - \infty ; + \infty )?\]

A. 7

B. 4

C. 6

D. 5

14. Tìm tất cả các giá trị của m để hàm số \(y = \frac{1}{3}{x^3} + (m + 1){x^2} - (m + 1)x + 1\) đồng biến trên tập xác định.

A. \(\left[ {\begin{array}{*{20}{l}}{m \ge  - 1}\\{m \le  - 2}\end{array}} \right.\).

B. \( - 2 < m <  - 1\).

C. \( - 2 \le m \le  - 1\).

D. \(\left[ {\begin{array}{*{20}{l}}{m >  - 1}\\{m <  - 2}\end{array}} \right.\).

15. Có bao nhiêu giá trị nguyên của m để hàm số \(y = \frac{1}{3}\left( {{m^2} - m} \right){x^3} - \left( {{m^2} - m} \right){x^2} + mx + 1\) đồng biến trên \(R\) ?

A. 1 .

B. 2 .

C. 3 .

D. vô số

16. Có bao nhiêu giá trị nguyên của m để hàm số \(y = \frac{1}{3}\left( {{m^2} - m} \right){x^3} - \left( {{m^2} - m} \right){x^2} + mx + 1\) đồng biến trên \(R\) ?

A. 1 .

B. 2 .

C. 3 .

D. vô số

17. Cho hàm số \(y = \frac{{mx - 2m - 3}}{{x - m}}\) vơi m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m đề hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S.

A. 5

B. 4

C. Vô số

D. 3

18. Cho hàm số \(y = \frac{{mx + 4m}}{{x + m}}\) với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.

A. 5

B. 4 ,

C. Vô số

D. 3

19. Tất cả các giá trị của m để hàm số \(y = \frac{{mx + 3}}{{3x + m}}\) nghịch biến trên từng khoảng xác định của hàm số là:

A. \(m <  - 3\) hoặc \(m > 3\).

B. \( - 3 \le m \le 3\).

C. \(m \le  - 3\) hoặc \(m \ge 3\).

D. \( - 3 < m < 3\)

Bài toán 3: Tìm m để hàm số đơn điệu trên 1 khoảng, nữa khoảng hoặc 1 đoạn bất kỳ

Dạng: \(y = f(x,m) = \frac{{ax + b}}{{cx + d}}\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ad - bc > 0( < 0)}\\{x =  - \frac{d}{c} \notin D}\end{array}} \right.\)

20. Giá trị của m để hàm số \(y = \frac{{mx - 16}}{{x - m}}\) nghịch biến trên khoảng (-1;5)

A. \(\left[ {\begin{array}{*{20}{l}}{m <  - 4}\\{m \ge 5}\end{array}.\quad } \right.\)

B. \(\left[ {\begin{array}{*{20}{l}}{m <  - 4}\\{m > 4}\end{array}} \right.\).

C.

\(\left[ {\begin{array}{*{20}{l}}{m \le  - 1}&{{\rm{ D}}{\rm{. }}4 < m \le 5}\\{m > 4}&{}\end{array}.} \right.\)

21. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 2}}{{x + 3m}}\) đồng biến trên khoảng \(( - \infty ; - 6)\) ?

A. 2 .

B. 6 .

C. Vô số.

D. 1 .

22. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 6}}{{x + 5m}}\) nghịch biến trên khoảng \((10; + \infty )\).

A. 3 .

B. Vô số.

C. 4 .

D. 5 .

23. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 1}}{{x + 3m}}\) nghịch biến trên khoảng \((6; + \infty )\) ?

A. 3 .

B. Vô số.

C. 0 .

D. 6 .

24. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 2}}{{x + 5m}}\) đồng biến trên khoảng \(( - \infty ; - 10)\) ?

A. 2 .

B. Vô số.

C. 1 .

D. 3 .

25. Trong tất cả các giá trị của m để hàm số \(y =  - \frac{1}{3}{x^3} + (m - 1){x^2} + (m + 3)x - 10\) đồng biến trên khoảng (0;3) thì \(m = {m_0}\) là giá trị nhỏ nhất. Giá trị \({m_0}\) là

A. 1,5 .

B. 1,6 .

C. 1,7 .

D. 1,8 .

26. Có bao nhiêu giá trị nguyên của m để hàm số \(y = \frac{2}{3}{x^3} - (2m - 3){x^2} + 2\left( {{m^2} - 3m} \right)x + 1\) nghịch biến trên khoảng (1;3)

A. 4 .

B. 1 .

C. 2 .

D. 3 .

27. Trong tất cả các giá trị của m để hàm số \(y =  - 2{x^3} + 3(m + 1){x^2} - 6mx - 1\) đồng biến trên (-2,0) thì \(m = {m_0}\) là giá trị lớn nhất. Hỏi các số sau đâu là số gần \({m_0}\) nhất:

A. 2 .

B. -1.

C. 4 .

D. -4.

Bài toán 4: Đặt ẩn phụ giải đơn điệu trên khoảng

28. Cho hàm số \(y = \frac{{(m - 1)\sqrt {x - 1}  + 2}}{{\sqrt {x - 1}  + m}}\). Tìm tất cả các giá trị của tham số m đề hàm số đồng biến trên (17; 27).

A. \(m \in [ - 4; - 1)\).

B. \(m \in ( - \infty ; - 6] \cup [ - 4; - 1) \cup (2; + \infty )\).

C. \(m \in ( - \infty ; - 4] \cup (2; + \infty )\).

D. \(m \in ( - 1;2)\).

29. Tất cả các giá trị thực của tham số m để hàm số \(\frac{{\sin x + m}}{{\sin x - m}}\) nghịch biến trong \(\left( {\frac{\pi }{2};\pi } \right)\) là:

A. \(m < 0\).

B. \(\left[ {\begin{array}{*{20}{l}}{m < 0}\\{m \ge 1}\end{array}} \right.\).

C. \(0 < m \le 1\).

D. \(m >  - 1\).

30. Tìm tất cả các giá trị của m để hàm số \(y = \frac{{\tan x - 2}}{{\tan x - m}}\) đồng biến trên \(\left( {0;\frac{\pi }{4}} \right):\)

A. \(m \le 0\) hoặc \(1 \le m < 2m < 0\).

B. \(m \le 0\).

C. \(1 \le m < 2\).

D. \(m \ge 2\).

31. Cho hàm số

\(y = {\left( {\sqrt {{x^2} + 1}  - x} \right)^3} - m\left( {2{x^2} - 2\sqrt {{x^2} + 1}  + 1} \right) - \frac{{(m - 6)}}{{\sqrt {{x^2} + 1}  + x}} - 1\).Có bao nhiêu giá trị nguyên dương của tham số m để hàm số đồng biến trên \(\mathbb{R}\) :

A. 5 .

B. Vô số.

C. 2 .

D. 3 .

32. Tìm tất cả các giá trị của m để hàm số \(y = \frac{{m - \sin x}}{{{{\cos }^2}x}}\) nghịch biến trên \(\left( {0;\frac{\pi }{6}} \right)\)

A. \(m > 1\).

B. \(m \le \frac{5}{2}\).

C. \(m \le \frac{5}{4}\).

D. \(m < 2\).