Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tính đơn điệu của hàm ẩn được cho bởi đồ thị hàm f'(x), tài liệu bao gồm 46 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tính đơn điệu của hàm ẩn cho bởi đồ thị hàm f’(x)

I. Kiến thức cần nhớ

1. Định nghĩa 1

Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và y = f(x) là một hàm số xác định trên K. Ta nói:

+ Hàm số y = f(x)  được gọi là đồng biến (tăng) trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)

+ Hàm số y = f(x)  được gọi là nghịch biến (giảm) trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\) Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.

2. Nhận xét

Nhận xét 1

Nếu hàm số f(x) và g(x) cùng đồng biến (nghịch biến) trên D thì hàm số f(x) + g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu f(x) - g(x) .

Nhận xét 2

Nếu hàm số f(x) và g(x)  là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số f(x). g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số f(x), g(x) không là các hàm số dương trên D.

Nhận xét 3

Cho hàm số u = u(x), xác định với \(x \in (a;b)\) và \(u(x) \in (c;d)\). Hàm số  f[u(x)] cũng xác định với \(x \in (a;b)\). Ta có nhận xét sau:

i. Giả sử hàm số u = u(x) đồng biến với \(x \in (a;b)\). Khi đó, hàm số f[u(x)] đồng biến với \(x \in (a;b) \Leftrightarrow f(u)\) đồng biến với \(u \in (c;d)\).

ii. Giả sử hàm số u = u(x) nghịch biến với \(x \in (a;b)\). Khi đó, hàm số f[u(x)] nghịch biến với \(x \in (a;b) \Leftrightarrow f(u)\) nghịch biến với \(u \in (c;d)\).

3. Định lý 1

Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:

a) Nếu hàm số đồng biến trên khoảng K thì \({f^\prime }(x) \ge 0,\forall x \in K\).

b) Nếu hàm số nghịch biến trên khoảng K thì \({f^\prime }(x) \le 0,\forall x \in K\).

4. Định lý 2

Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:

a) Nếu \({f^\prime }(x) > 0,\forall x \in K\) thì hàm số f đồng biến trên K.

b) Nếu \({f^\prime }(x) < 0,\forall x \in K\) thì hàm số f nghịch biến trên K.

c) Nếu \({f^\prime }(x) = 0,\forall x \in K\) thì hàm số f không đổi trên K.

Chú ý

Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có thêm giả thuyết " Hàm số liên tục trên đoạn hoặc nửa khoảng đó'. Chẳng hạn:

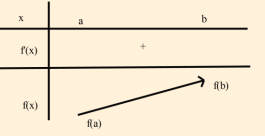
Nếu hàm số f liên tục trên đoạn [a ; b] và \({f^\prime }(x) > 0,\forall x \in (a;b)\) thì hàm số f đồng biến trên đoạn [a ; b].

5. Định lý 3

Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:

a) Nếu \({f^\prime }(x) \ge 0,\forall x \in K\) và \({f^\prime }(x) = 0\) chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.

b) Nếu \({f^\prime }(x) \le 0,\forall x \in K\) và \({f^\prime }(x) = 0\) chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.

Quy tắc xét tính đơn điệu của hàm số.

Giả sử hàm số f có đạo hàm trên K

- Nếu \({f^\prime }(x) \ge 0\) với mọi \(x \in K\) và \({f^\prime }(x) = 0\) chỉ tại một số hữu hạn điểm \(x \in K\) thì hàm số f đồng biến trên K.

- Nếu \({f^\prime }(x) \le 0\) với mọi \(x \in K\) và \({f^\prime }(x) = 0\) chỉ tại một số hữu hạn điểm \(x \in K\) thì hàm số f nghịch biến trên K.

II. Bài tập mẫu

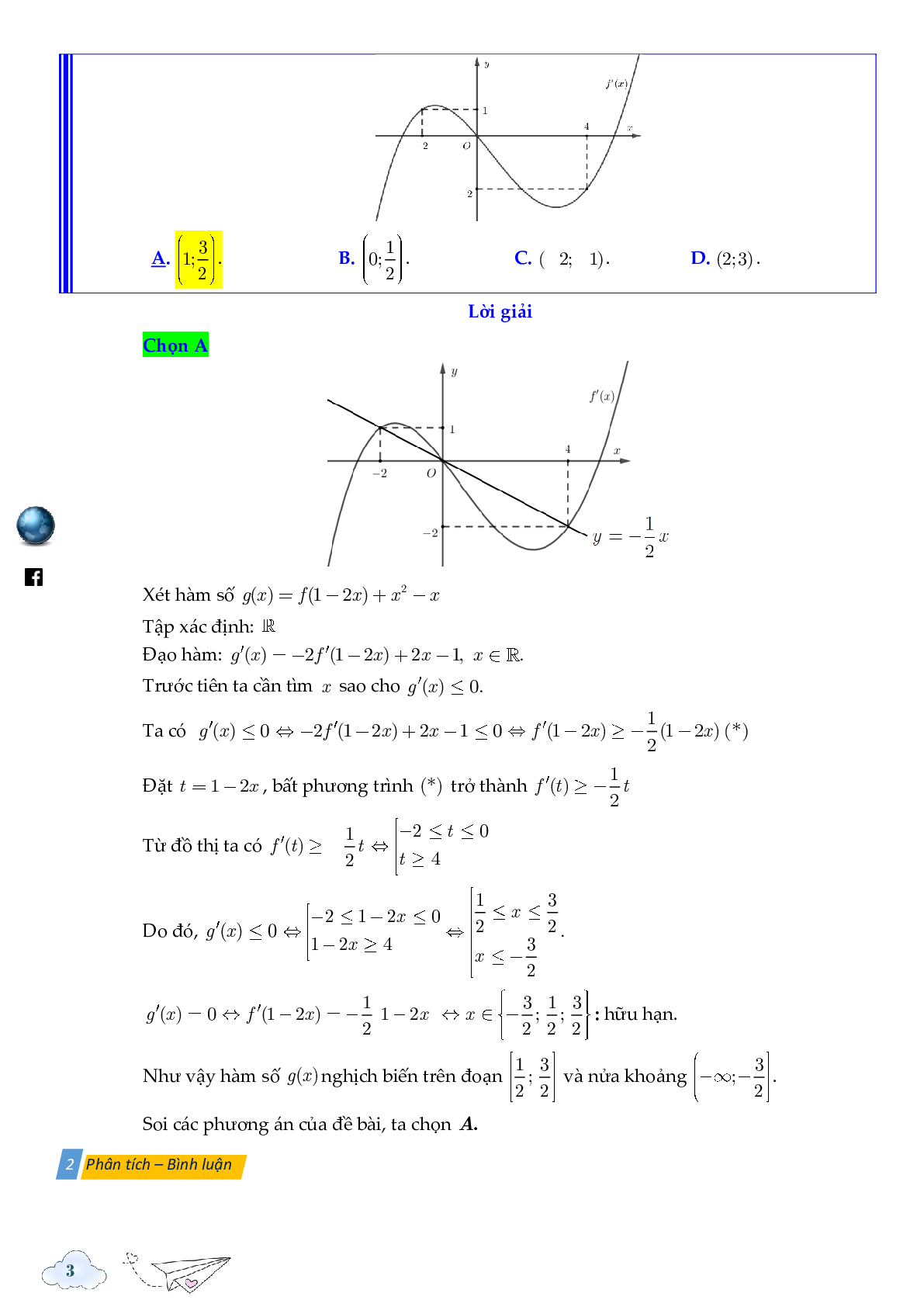
Câu 50. Cho hàm số y = f(x). Hàm số \(y = {f^\prime }(x)\) có đồ thị như hình vẽ bên dưới. Hàm số \(g(x) = f(1 - 2x) + {x^2} - x\) nghịch biến trên khoảng nào dưới đây?

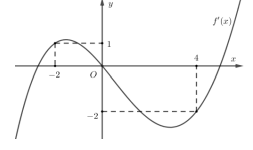
A. \(\left( {1;\frac{3}{2}} \right)\).

B. \(\left( {0;\frac{1}{2}} \right)\).

C. \(( - 2; - 1)\).

D. \((2;3)\).

Lời giải

Chọn A

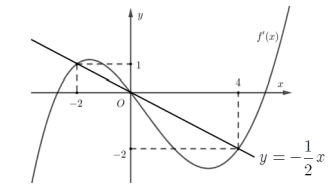
Xét hàm số \(g(x) = f(1 - 2x) + {x^2} - x\)

Tập xác định: \(\mathbb{R}\)

Đạo hàm: \({g^\prime }(x) =  - 2{f^\prime }(1 - 2x) + 2x - 1,x \in \mathbb{R}\).

Trước tiên ta cân tìm \(x\) sao cho \({g^\prime }(x) \le 0\).

Ta có

\(\begin{array}{l}{g^\prime }(x) \le 0 \Leftrightarrow  - 2{f^\prime }(1 - 2x) + 2x - 1 \le 0\\ \Leftrightarrow {f^\prime }(1 - 2x) \ge  - \frac{1}{2}(1 - 2x)(*)\end{array}\)

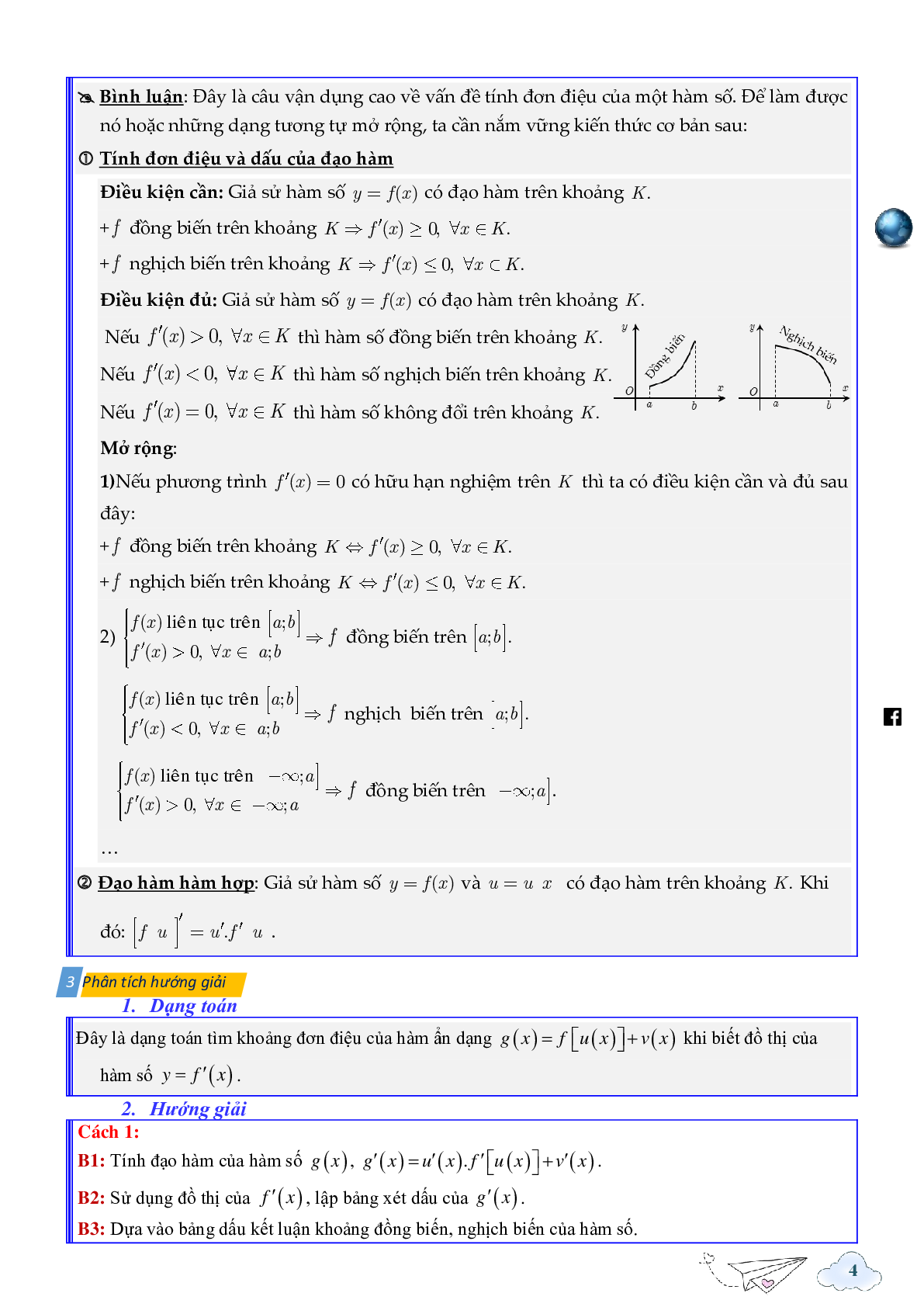
Đặt \(t = 1 - 2x\), bất phương trình (*) trở thành \({f^\prime }(t) \ge  - \frac{1}{2}t\)

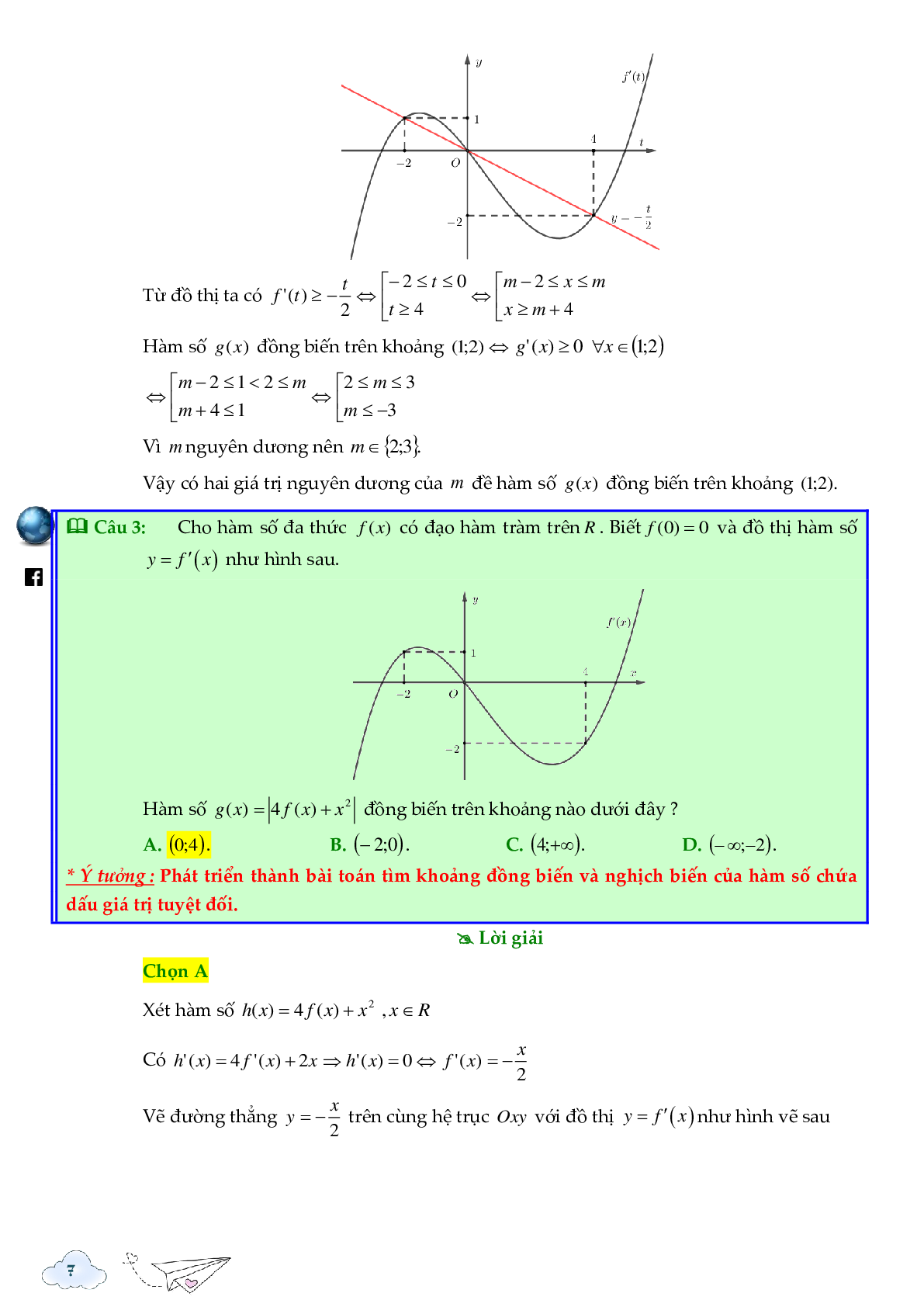
Từ đồ thị ta có \({f^\prime }(t) \ge  - \frac{1}{2}t \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 2 \le t \le 0}\\{t \ge 4}\end{array}} \right.\)

Do đó, \({g^\prime }(x) \le 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 2 \le 1 - 2x \le 0}\\{1 - 2x \ge 4}\end{array}} \right.\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\frac{1}{2} \le x \le \frac{3}{2}}\\{x \le  - \frac{3}{2}}\end{array}} \right.\)

\({g^\prime }(x) = 0 \Leftrightarrow {f^\prime }(1 - 2x) =  - \frac{1}{2}1 - 2x \Leftrightarrow x \in \left\{ { - \frac{3}{2};\frac{1}{2};\frac{3}{2}} \right\}\) : hữu hạn.

Như vậy hàm số g(x) nghịch biến trên đoạn \(\left[ {\frac{1}{2};\frac{3}{2}} \right]\) và nửa khoảng \(\left( { - \infty ; - \frac{3}{2}} \right]\).

Soi các phương án của đề bài, ta chọn A.

Bình luận : Đây là câu vận dụng cao về vấn đề tính đơn điệu của 1 hàm số. Để làm được nó hoặc những dạng tương tự mở rộng, ta cần nắm vững kiến thức cơ bản sau:

(1) Tính đơn điệu và dấu của đạo hàm

Điều kiện cần: Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.

+ f đồng biến trên khoảng \(K \Rightarrow {f^\prime }(x) \ge 0,\forall x \in K\).

+ f nghịch biến trên khoảng \(K \Rightarrow {f^\prime }(x) \le 0,\forall x \in K\).

Điều kiện đủ: Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.

Nếu \({f^\prime }(x) > 0,\forall x \in K\) thì hàm số đồng biến trên khoảng K.

Nếu \({f^\prime }(x) < 0,\forall x \in K\) thì hàm số nghịch biến trên khoảng K.

Nếu \({f^\prime }(x) = 0,\forall x \in K\) thì hàm số không đổi trên khoảng K.

Mở rộng:

1)Nếu phương trình \({f^\prime }(x) = 0\) có hữu hạn nghiệm trên K thì ta có điêu kiện cân và đủ sau đây:

+ f  đồng biến trên khoảng \(K \Leftrightarrow {f^\prime }(x) \ge 0,\forall x \in K\).

+ f  nghịch biến trên khoảng \(K \Leftrightarrow {f^\prime }(x) \le 0,\forall x \in K\).

2) \(\left\{ {\begin{array}{*{20}{l}}{f(x){\rm{ li\^e n t?c tr\^e n }}[a;b]}\\{{f^\prime }(x) > 0,\forall x \in a;b}\end{array} \Rightarrow f} \right.\) đồng biến trên [a ; b]

\(\left\{ {\begin{array}{*{20}{l}}{f(x){\rm{ li\^e n tuc tr\^e n }}[a;b]}\\{{f^\prime }(x) < 0,\forall x \in a;b}\end{array} \Rightarrow f} \right.\) nghịch biến trên [a ; b] .

 \(\left\{ {\begin{array}{*{20}{l}}{f(x){\rm{ li\^e n tuc tr\^e n }} - \infty ;a]}\\{{f^\prime }(x) > 0,\forall x \in  - \infty ;a}\end{array} \Rightarrow f} \right.\) đông biến trên \(\left. { - \infty ;a} \right].\)

(2) Đạo hàm hàm hợp: Giả sử hàm số y = f(x) và \(u = u\quad x\) có đạo hàm trên khoảng K. Khi đó: \({[fu]^\prime } = {u^\prime } \cdot {f^\prime }u\).

1. Dạng toán

Đây là dạng toán tìm khoảng đơn điệu của hàm ẩn dạng \(g(x) = f[u(x)] + v(x)\) khi biết đồ thị của hàm số \(y = {f^\prime }(x)\).

2. Hướng giải

Cách 1:

B1: Tính đạo hàm của hàm số \(g(x),{g^\prime }(x) = {u^\prime }(x) \cdot {f^\prime }[u(x)] + {v^\prime }(x)\).

B2: Sử dụng đồ thị của \({f^\prime }(x)\), lập bảng xét dấu của \({g^\prime }(x)\).

B3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.

Cách 2:

B1: Tính đạo hàm của hàm số \(g(x),{g^\prime }(x) = {u^\prime }(x) \cdot {f^\prime }[u(x)] + {v^\prime }(x)\).

B2: Hàm số g(x) đồng biến \( \Leftrightarrow {g^\prime }(x) \ge 0\); (Hàm số \(g(x)\) nghịch biến \(\left. { \Leftrightarrow {g^\prime }(x) \le 0} \right)(*)\)

B3: Giải bất phương trình \((*)\) (dựa vào đồ thị hàm số \(y = {f^\prime }(x)\) ) từ đó kết luận khoảng đồng biến, nghịch biến của hàm số.

Cách 3: (Trắc nghiệm)

B1: Tính đạo hàm của hàm số \(g(x),{g^\prime }(x) = {u^\prime }(x) \cdot {f^\prime }[u(x)] + {v^\prime }(x)\).

B2: Hàm số \(g(x)\) đồng biến trên \(K \Leftrightarrow {g^\prime }(x) \ge 0,\forall x \in K\); (Hàm số g(x) nghịch biến trên \(K\) \(\left. { \Leftrightarrow {g^\prime }(x) \le 0,\forall x \in K} \right)(*)\)

B3: Lần lượt chọn thay giá trị từ các phương án vào \({g^\prime }(x)\) để loại các phương án sai.

III. Bài tập tương tự và phát triển

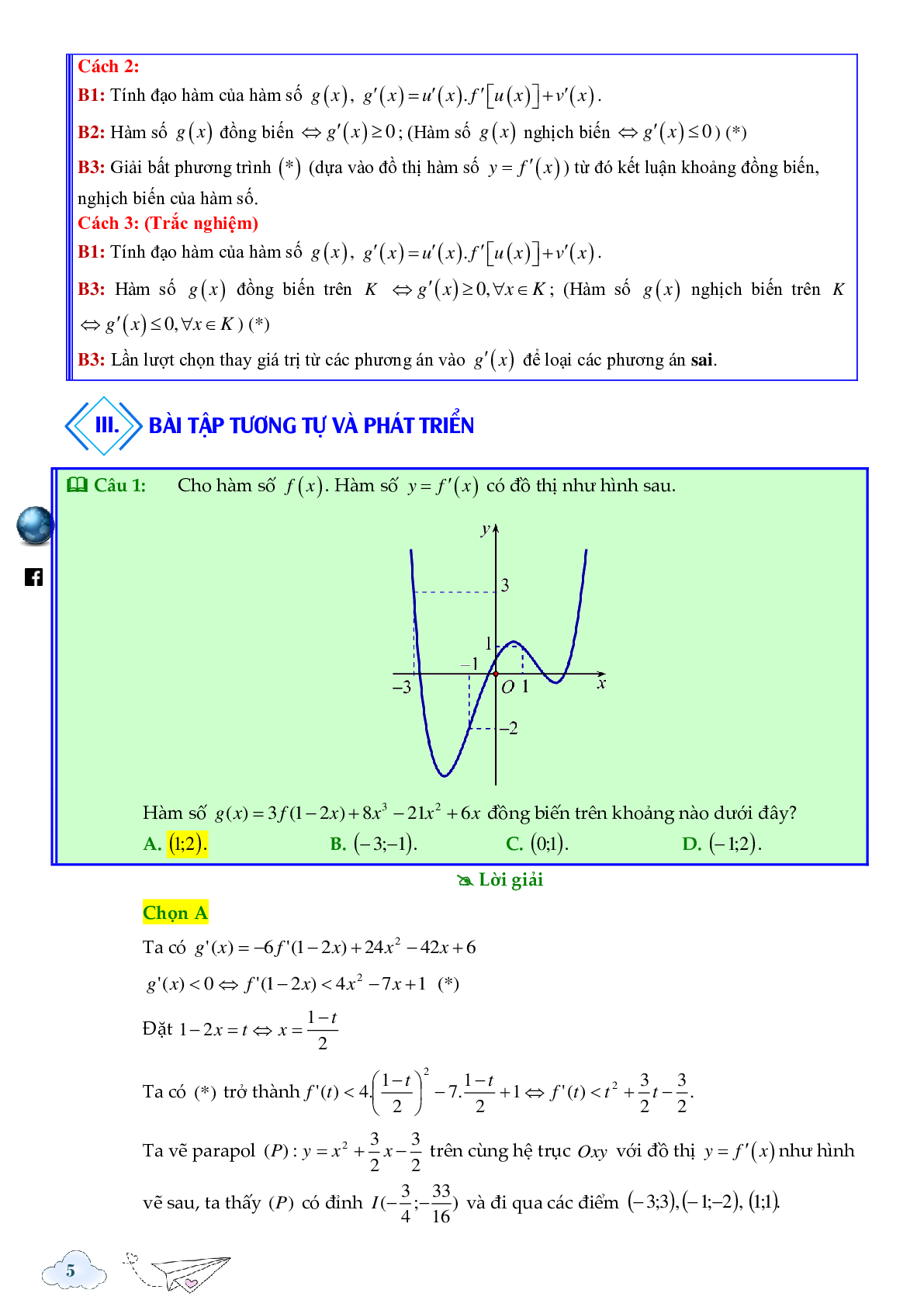
Câu 1: Cho hàm số f(x). Hàm số \(y = {f^\prime }(x)\) có đồ thị như hình sau.

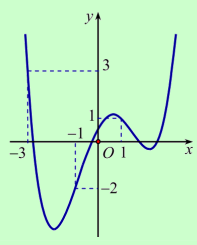
Hàm số \(g(x) = 3f(1 - 2x) + 8{x^3} - 21{x^2} + 6x\) đồng biến trên khoảng nào dưới đây?

A. (1;2).

B. (-3;-1).

C. (0;1).

D. (-1; 2).

Lời giải

Chọn A

Ta có \({g^\prime }(x) =  - 6{f^\prime }(1 - 2x) + 24{x^2} - 42x + 6\)

\({g^\prime }(x) < 0 \Leftrightarrow {f^\prime }(1 - 2x) < 4{x^2} - 7x + 1\quad (*)\)

Đặt \(1 - 2x = t \Leftrightarrow x = \frac{{1 - t}}{2}\)

Ta có \((*)\) trở thành

\(\begin{array}{l}{f^\prime }(t) < 4 \cdot {\left( {\frac{{1 - t}}{2}} \right)^2} - 7 \cdot \frac{{1 - t}}{2} + 1\\ \Leftrightarrow {f^\prime }(t) < {t^2} + \frac{3}{2}t - \frac{3}{2}\end{array}\).

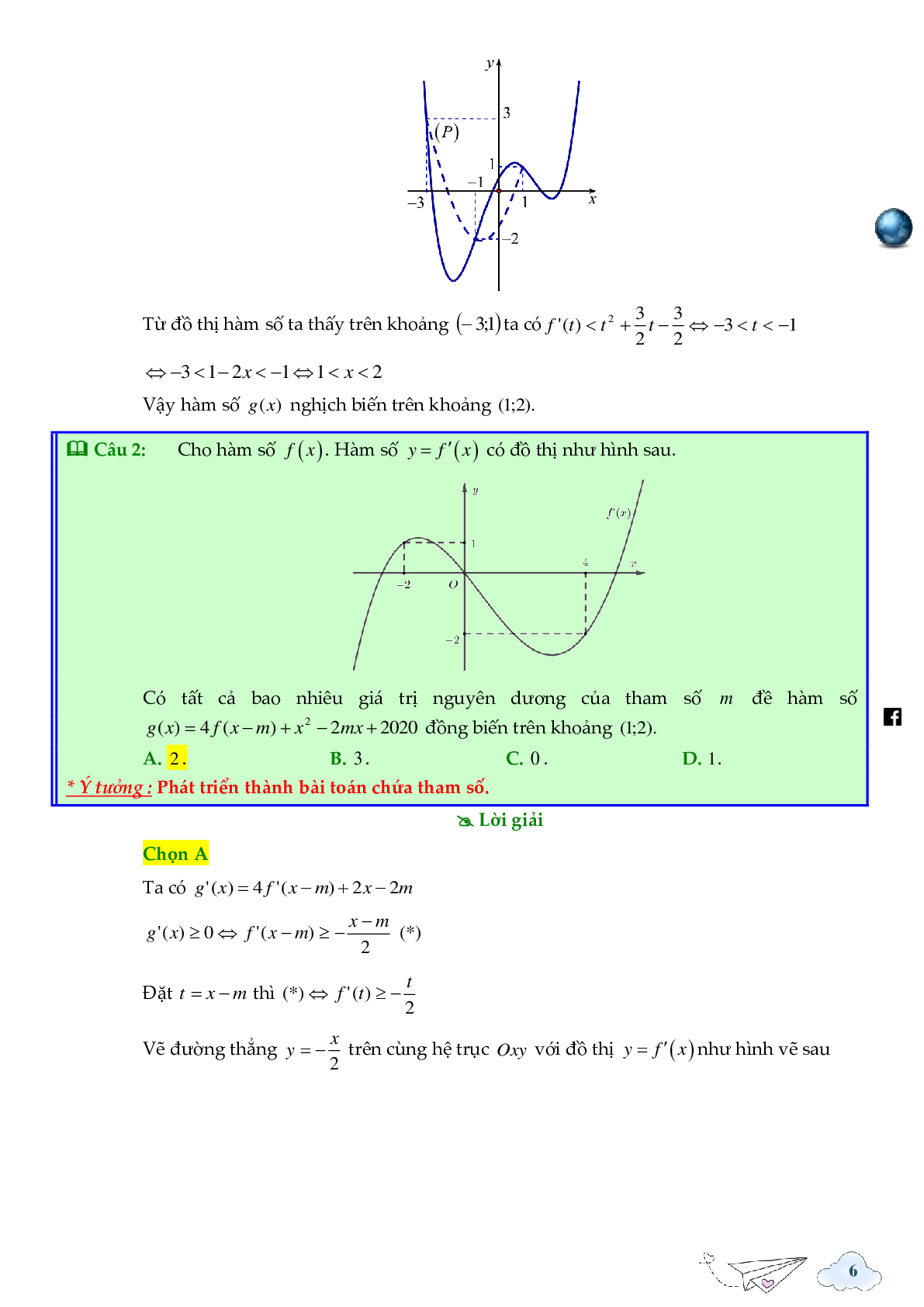
Ta vẽ parapol \((P):y = {x^2} + \frac{3}{2}x - \frac{3}{2}\) trên cùng hệ trục Oxy với đồ thị \(y = {f^\prime }(x)\) như hình vẽ sau, ta thấy (P) có đỉnh \(I\left( { - \frac{3}{4}; - \frac{{33}}{{16}}} \right)\) và đi qua các điểm \(( - 3;3),( - 1; - 2),(1;1)\).

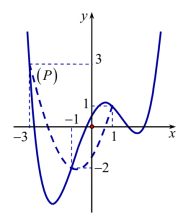
Từ đồ thị hàm số ta thấy trên khoảng (-3;1) ta có

\({f^\prime }(t) < {t^2} + \frac{3}{2}t - \frac{3}{2} \Leftrightarrow  - 3 < t <  - 1\)

\( \Leftrightarrow  - 3 < 1 - 2x <  - 1 \Leftrightarrow 1 < x < 2\)

Vậy hàm số g(x) nghịch biên trên khoảng (1;2).