Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 54 câu trắc nghiệm ôn tập chuyên đề Hàm số, tài liệu bao gồm 8 trang, 54 câu trắc nghiệm. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

54 câu trắc nghiệm ôn tập chuyên đề Hàm số

Chương 1 Hàm số từ A – Z

Câu 1. Cho hàm số \(y =  - {x^3} + 3{x^2} - 3x + 2\). Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số nghịch biến trên \(\mathbb{R}\).

B. Hàm số nghịch biến trên các khoảng \(( - \infty ;1)\) vả \((1; + \infty )\).

C. Hàm số đồng biến trên khoảng \(( - \infty ;1)\) và nghịch biến trên khoảng \((1; + \infty )\).

D. Hàm số đồng biến trên \(\mathbb{R}\).

Câu 2. Cho hàm số \(y = \frac{{x + 1}}{{1 - x}}\). Khẳng định nào sao đây là khẳng định đúng?

A. Hàm số nghịch biến trên khoảng \(( - \infty ;1) \cup (1; + \infty )\).

B. Hàm số đồng biến trên khoảng \(( - \infty ;1) \cup (1; + \infty )\).

C. Hàm số nghịch biến trên các khoảng \(( - \infty ;1)\) và \((1; + \infty )\).

D. Hàm số đồng biến trên các khoảng \(( - \infty ;1)\) và \((1; + \infty )\).

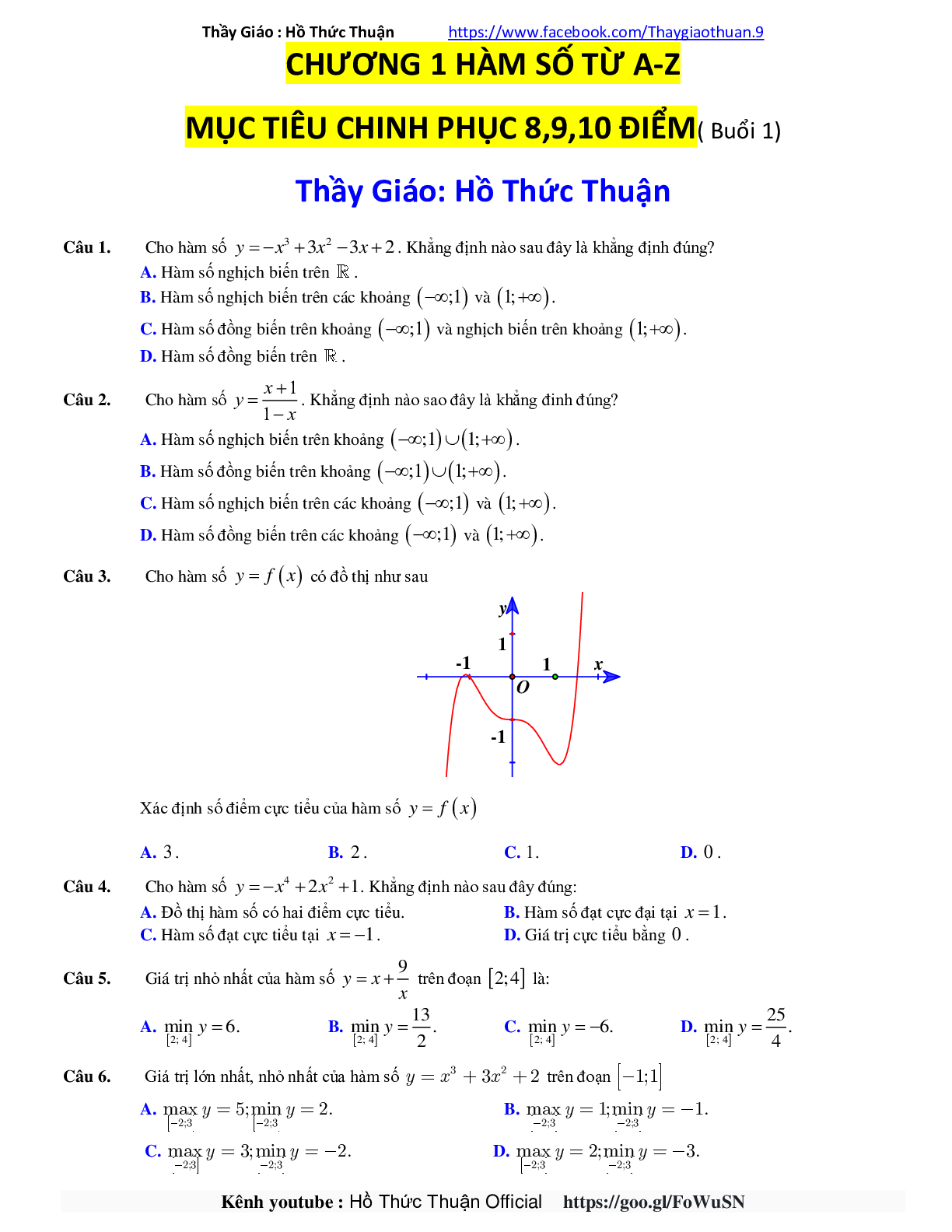
Câu 3. Cho hàm số y  = f(x) có đồ thị như sau

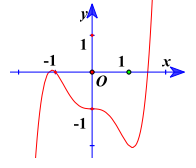
Xác định số điểm cực tiểu của hàm số y = f(x)

A. 3

B. 2

C. 0

D. 1

Câu 4. Cho hàm số \(y =  - {x^4} + 2{x^2} + 1\). Khẳng định nào sau đây đúng:

A. Đồ thị hàm số có hai điểm cực tiểu.

B. Hàm số đạt cực đại tại x = 1.

C. Hàm số đạt cực tiểu tại x = - 1.

D. Giá trị cực tiểu bằng 0 .

Câu 5. Giá trị nhỏ nhất của hàm số \(y = x + \frac{9}{x}\) trên đoạn [2 ; 4] là:

A. \({\min _{[2;4]}}y = 6\).

B. \({\min _{[2;4]}}y = \frac{{13}}{2}\).

C. \({\min _{[2;4]}}y =  - 6\).

D. \({\min _{[2;4]}}y = \frac{{25}}{4}\).

Câu 6. Giá trị lớn nhất, nhỏ nhất của hàm số \(y = {x^3} + 3{x^2} + 2\) trên đoạn [ -1;1]

A. \({\max _{\mid  - 2;3\} }}y = 5;{\min _{| - 2;3|}}y = 2\).

B. \({\max _{\mid  - 2;3\} }}y = 1;{\min _{\mid  - 2;3]}}y =  - 1\).

C. \({\max _{| - 2;3|}}y = 3;{\min _{| - 2:3|}}y =  - 2\).

D. \({\max _{\mid  - 2;3\} }}y = 2;{\min _{[ - 2;3]}}y =  - 3\).

Câu 7. Đồ thị hàm số \(y = \frac{{2x - 3}}{{x - 1}}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

A. \(x = 1\) và \(y =  - 3\).

B. \(x = 2\) và \(y = 1\).

C. \(x = 1\) và \(y = 2\).

D. \(x =  - 1\) và \(y = 2\).

Câu 8. Cho hàm số \(y = fx\) có \(\mathop {\lim }\limits_{x \to  + \infty } fx = 1\) và \(\mathop {\lim }\limits_{x \to  - \infty } fx =  - 1\). Khẳng định nào sau đây là đúng?

A. Đồ thị đã cho không có tiệm cận ngang.

B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.

C. Đồ thị đã cho có hai tiệm cận ngang là các đường thẳng \(y = 1\) và \(y =  - 1\).

D. Đồ thị đã cho có hai tiệm cận ngang là các đường thẳng \(x = 1\) và \(x =  - 1\).

Câu 9. Đồ thị hàm số nào có tiệm cận đứng?

A. \(y = \frac{x}{{{x^2} + 1}}\).

B. \(y =  - {x^3} - 3{x^2} - 1\).

C. \(y = \frac{{{x^2} - 2x}}{3}\).

D. \(y = \frac{{{x^2} - 2x + 1}}{{x - 3}}\).

Câu 10. Các khoảng đồng biến của hàm số \(y = {x^3} - 5{x^2} + 7x - 3\) là

A. \( - \infty ;1\) và \(\left( {\frac{7}{3}; + \infty } \right)\).

B. \(\left( {1;\frac{7}{3}} \right)\).

C. [-5;7].

D. 7 ; 3

Câu 11. Hàm số \(y =  - {x^3} + 6{x^2} - 9x\) có các khoảng nghịch biến là:

A. \(( - \infty ; + \infty )\).

B. \(( - \infty ; - 4);(0; + \infty )\).

C.1 ; 3$.

D. \(( - \infty ;1);(3; + \infty )\).

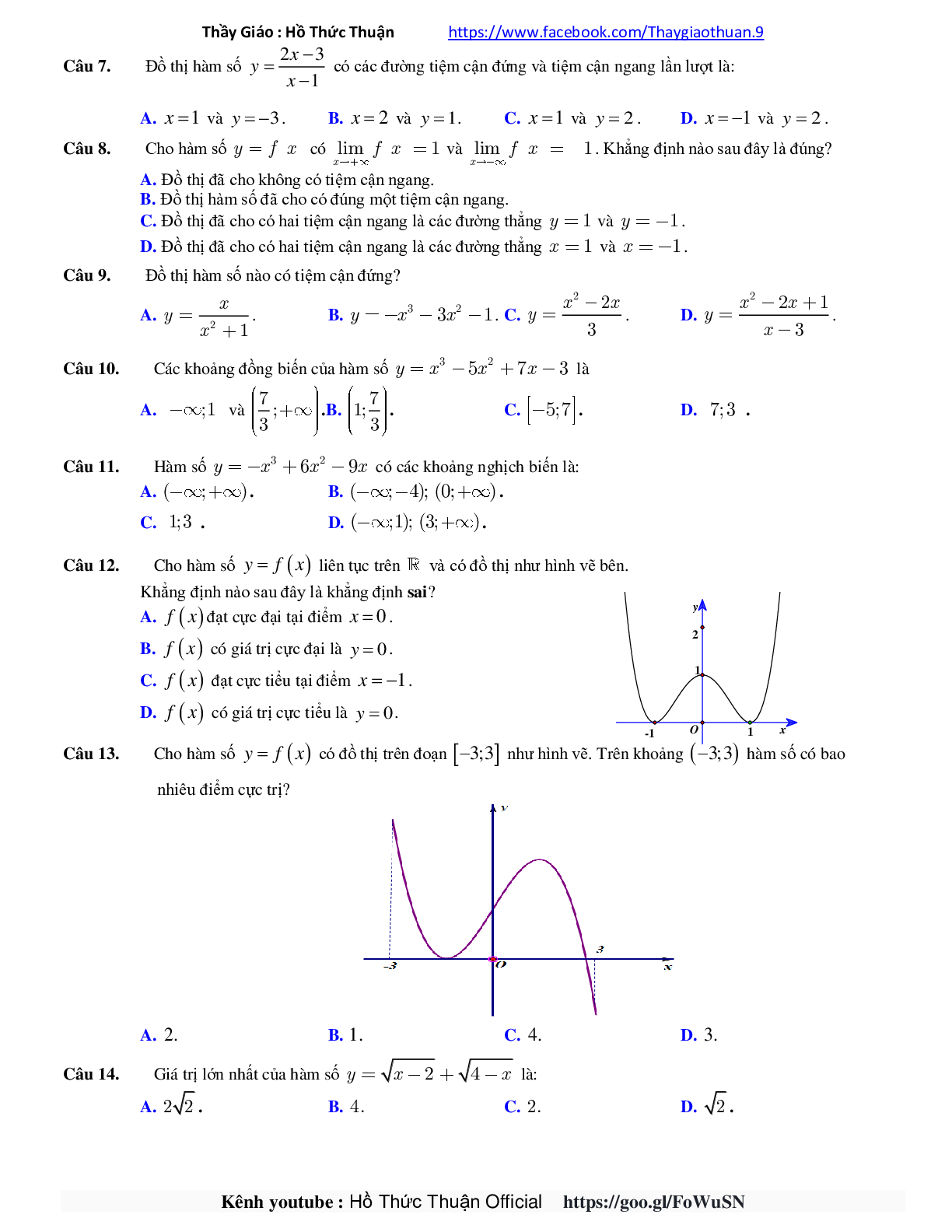
Câu 12. Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên.

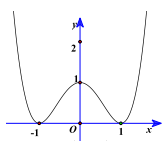
Khẳng định nào sau đây là khẳng định sai?

A. f(x)  đạt cực đại tại điểm x = 0.

B. f(x)  có giá trị cực đại là y = 0.

C. f(x)  đạt cực tiểu tại điểm x = -1.

D. f(x)  có giá trị cực tiểu là y = 0.

Câu 13. Cho hàm số y = f(x) có đồ thị trên đoạn [-3;3] như hình vẽ. Trên khoảng (-3;3) hàm số có bao nhiêu điểm cực trị?

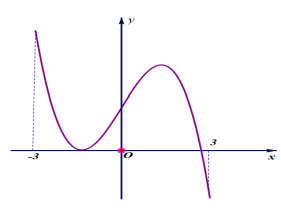
A. 2 .

B. 1 .

C. 4 .

D. 3 .

Câu 14. Giá trị lớn nhất của hàm số \(y = \sqrt {x - 2}  + \sqrt {4 - x} \) là:

A. \(2\sqrt 2 \).

B. 4 .

C. 2 .

D. \(\sqrt 2 \).

Câu 15. Kết luận nào là đúng về giá trị lớn nhất và nhỏ nhất của hàm số \(y = \sqrt {2x - {x^2}} \) ?

A. Hàm số có giá trị lớn nhất và có giá trị nhỏ nhất.

B. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.

C. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất.

D. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.

Câu 16. Giá trị lớn nhất và nhỏ nhất của hàm số \(y = x\sqrt {1 - {x^2}} \) bằng:

A. \(\min y = 0;\max y = \frac{1}{2}\).

B. \(\min y =  - \frac{1}{2};\max y = \frac{1}{2}\).

C. \(\min y =  - \frac{1}{{\sqrt 2 }};\max y = \frac{1}{{\sqrt 2 }}\).

D. \(\min y = 0;\max y = \frac{1}{{\sqrt 2 }}\).

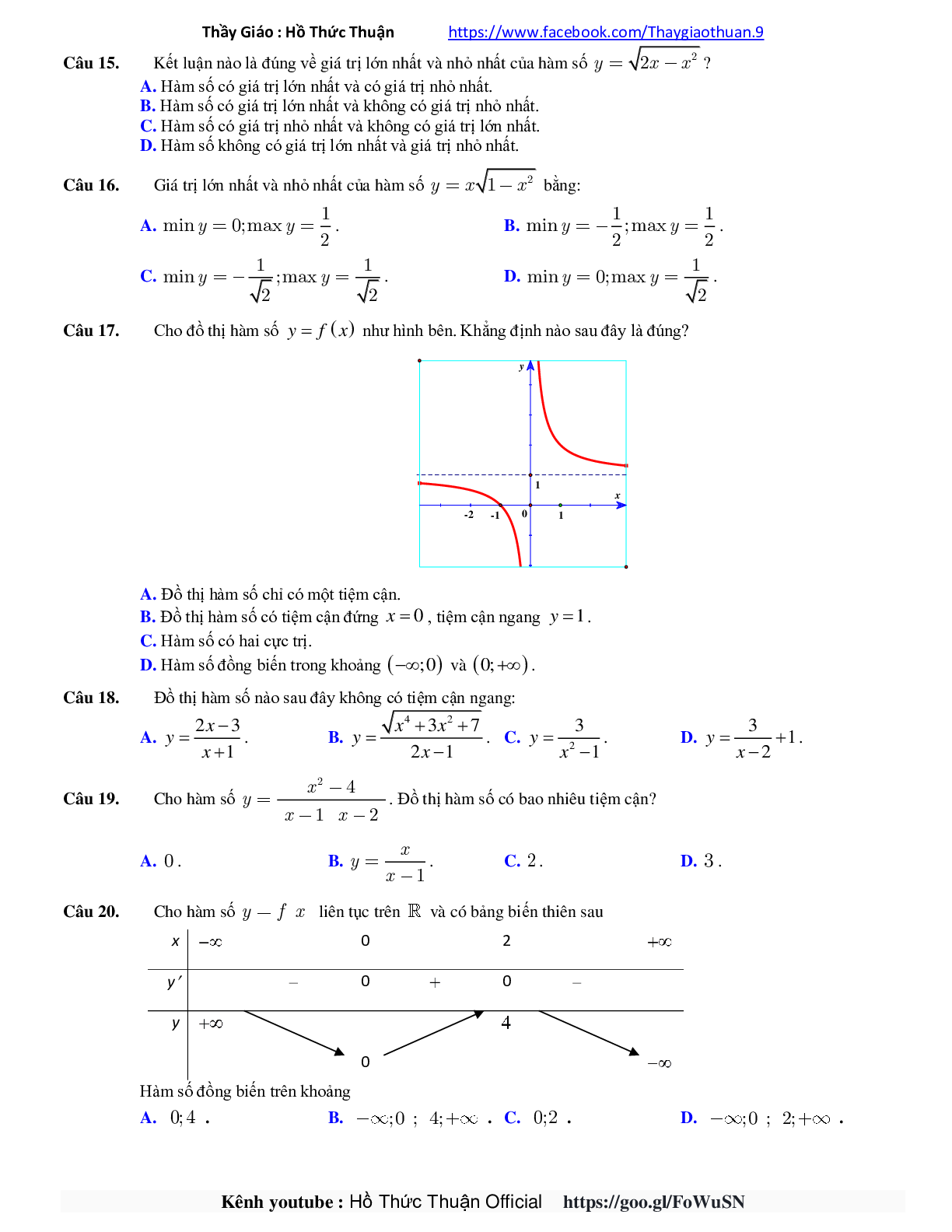
Câu 17. Cho đồ thị hàm số y = f(x) như hình bên. Khẳng định nào sau đây là đúng?

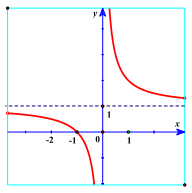
A. Đồ thị hàm số chỉ có một tiệm cận.

B. Đồ thị hàm số có tiệm cận đứng x = 0, tiệm cận ngang y = 1.

C. Hàm số có hai cực trị.

D. Hàm số đồng biến trong khoảng \(( - \infty ;0)\) và \((0; + \infty )\).

Câu 18. Đồ thị hàm số nào sau đây không có tiệm cận ngang:

A. \(y = \frac{{2x - 3}}{{x + 1}}\).

B. \(y = \frac{{\sqrt {{x^4} + 3{x^2} + 7} }}{{2x - 1}}\).

C. \(y = \frac{3}{{{x^2} - 1}}\).

D. \(y = \frac{3}{{x - 2}} + 1\).

Câu 19. Cho hàm số \(y = \frac{{{x^2} - 4}}{{x - 1\quad x - 2}}\). Đồ thị hàm số có bao nhiêu tiệm cận?

A. 0 .

B. \(y = \frac{x}{{x - 1}}\).

C. 2 .

D. 3 .

Câu 20. Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau

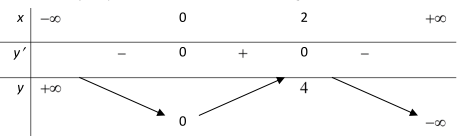
Hàm số đồng biến trên khoảng

A.0 ; 4.

B. \( - \infty ;0;4; + \infty \).

C. 0 ; 2.

D. \( - \infty ;0;2; + \infty \).

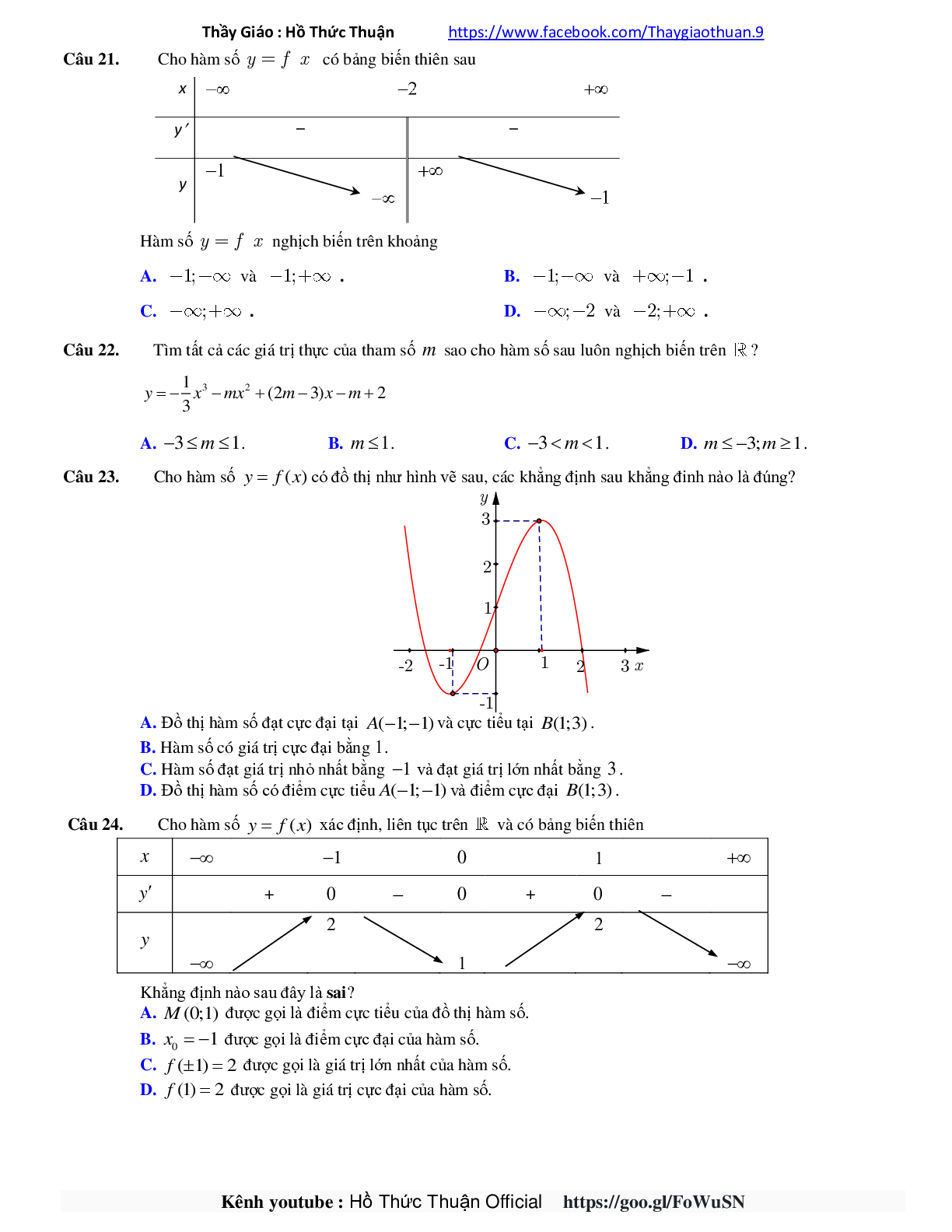
Câu 21. Cho hàm số y = f(x) có bảng biến thiên sau

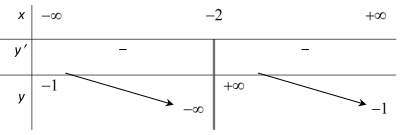
Hàm số y=f(x) nghịch biến trên khoảng

A. \( - 1; + \infty \) và \( - 1; + \infty \).

B. \( - 1; - \infty \) và \( + \infty ; - 1\).

C. \( - \infty ; + \infty \).

D. \( - \infty ; - 2\) và \( - 2; + \infty \).

Câu 22. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên \(\mathbb{R}\) ?

\(y =  - \frac{1}{3}{x^3} - m{x^2} + (2m - 3)x - m + 2\)

A. \( - 3 \le m \le 1\).

B. \(m \le 1\).

C. \( - 3 < m < 1\).

D. \(m \le  - 3;m \ge 1\).

Câu 23. Cho hàm số y = f(x) có đồ thị như hình vẽ sau, các khẳng định sau khẳng đinh nào là đúng?

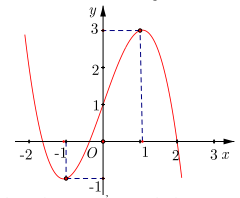
A. Đồ thị hàm số đạt cực đại tại A( -1;-1) và cực tiểu tại B(1;3).

B. Hàm số có giá trị cực đại bằng 1 .

C. Hàm số đạt giá trị nhỏ nhất bằng -1 và đạt giá trị lớn nhất bằng 3 .

D. Đồ thị hàm số có điểm cực tiểu A( -1;-1)  và điểm cực đại B(1;3).

Câu 24. Cho hàm số y = f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên

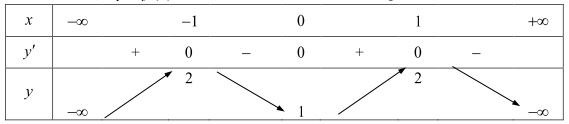
Khẳng định nào sau đây là sai?

A. M(0;1) được gọi là điểm cực tiểu của đồ thị hàm số.

B. \({x_0} =  - 1\) được gọi là điểm cực đại của hàm số.

C. \(f( \pm 1) = 2\) được gọi là giá trị lớn nhất của hàm số.

D. \(f(1) = 2\) được gọi là giá trị cực đại của hàm số.

Câu 25. Cho hàm số y = f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như sau

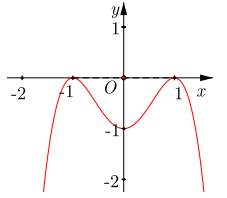
Khẳng định nào sau đây là khẳng định sai:

A. Hàm số có ba cực trị.

B. Hàm số có giá trị cực tiểu bằng -1.

C. Hàm số đạt cực đại tại x = 0

D. Đồ thị hàm số đi qua điểm A(0;-1).

Câu 26. Cho hàm số y = f(x) xác định và liên tục trên đoạn [-2,2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt GTLN trên đoạn [-2,2]  tại điểm nào sau đây?

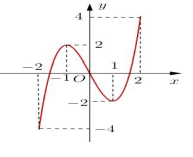
A. x = - 2.

B. x = - 1.

C. x = 1.

D. x = 2.

Câu 27. Hàm số \(y = \sqrt 3 \sin x + \cos x\) có giá trị lớn nhât, giá trị nhỏ nhât lần lượt là:

A. 0;-1.

B. \(\sqrt 3 ;0\).

C. \(\sqrt 3 ; - 1\).

D. 2, - 2.

Câu 28. Giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} - 3x + 6}}{{x - 1}}\) trên \(1; + \infty \) bằng:

A. 1 .

B. -1.

C. 3 .

D. 4 .

Câu 29. Tiệm cận ngang của đồ thị hàm số \(y = \frac{{\sqrt {{x^2} + x + 1} }}{{|x| - 3}}\)

A. y =1.

B. y =-1.

C. \(y =  \pm 1\).

D. x = 1.

Câu 30. Cho hàm số y = f(x) có bảng biến thiên dưới đây.

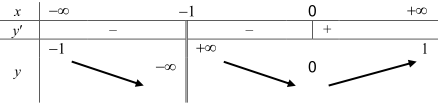
Khẳng định nào sau đây và khẳng định đúng?

A. Đồ thị hàm số có 3 đường tiệm cận.

B. Hàm số nghịch biến trên các khoảng \(( - \infty ;0)\) và \((0; + \infty )\).

C. Đồ thị hàm số không có tiệm cận.

D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0 .

Câu 31. Cho hàm số \(y = \frac{{\sqrt {{x^2} - x + 3}  - \sqrt {2x + 1} }}{{{x^3} - 2{x^2} - x + 2}}\). Trong các khẳng định sau, khẳng định nào là khẳng định đúng?

A. Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.

B. Đồ thị hàm số không có tiệm cận đứng và có đúng 1 tiệm cận ngang.

C. Đồ thị hàm số có đúng 3 tiệm cận đứng và 2 tiệm cận ngang.

D. Đồ thị hàm số có đúng 2 tiệm cận đứng và 1 tiệm cận ngang.

Câu 32. Cho hàm số y = f(x)  liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau. Khẳng định nào sau đây là SAI?

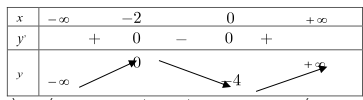
A. Hàm số đồng biến trên khoảng \((0; + \infty )\). \(\quad \)

B. Hàm số đạt cực tiểu tại x = 0.

C. Hàm số đạt cực tiểu tại x = - 2.

D. Hàm số nghịch biến trên khoảng ( - 2;0).

Câu 33. Cho hàm số y = f(x)  có đồ thị như hình vẽ bên.

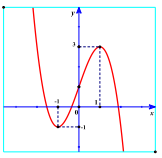
Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng -1;1.

B. Hàm số đồng biến trên khoảng -1;3.

C. Hàm số đồng biến trên khoảng \( - \infty ; - 1\) và \(1; + \infty \).

D. Hàm số đồng biến trên khoảng -1;1.

Câu 34. Tìm tất cả các giá trị của m để hàm số \(y = \frac{{mx + 1}}{{x + m}}\) đồng biến trên từng khoảng xác định của nó.

A. \(m \le  - 1\) hoặc \(m > 1\).

B. \(m <  - 1\) hoặc \(m > 1\).

C. \(m <  - 1\) hoặc \(m \ge 1\).

D. \( - 1 < m < 1\)

Câu 35. Cho hàm số y = f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên:

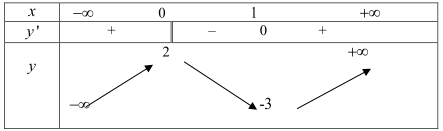
A. Hàm số có đúng một cực trị.

B. Hàm số có giá trị cực tiểu bằng 2 .

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3.

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.

Câu 36. Cho hàm số y = f(x)  có đạo hàm \({f^\prime }(x) = (x - 1)\left( {{x^2} - 2} \right)\left( {{x^4} - 4} \right)\). Số điểm cực trị của hàm số y = f(x)  là

A. 3 .

B. 2 .

C. 4 .

D. 1 .

Câu 37. Cho hàm số y = f(x)  có đạo hàm là \({f^\prime }(x) = x{(x + 1)^2}(x - 1)\). Hàm số y = f(x)  có bao nhiêu điểm cực trị?

A. 1 .

B. 3 .

C. 2 .

D. 0 .

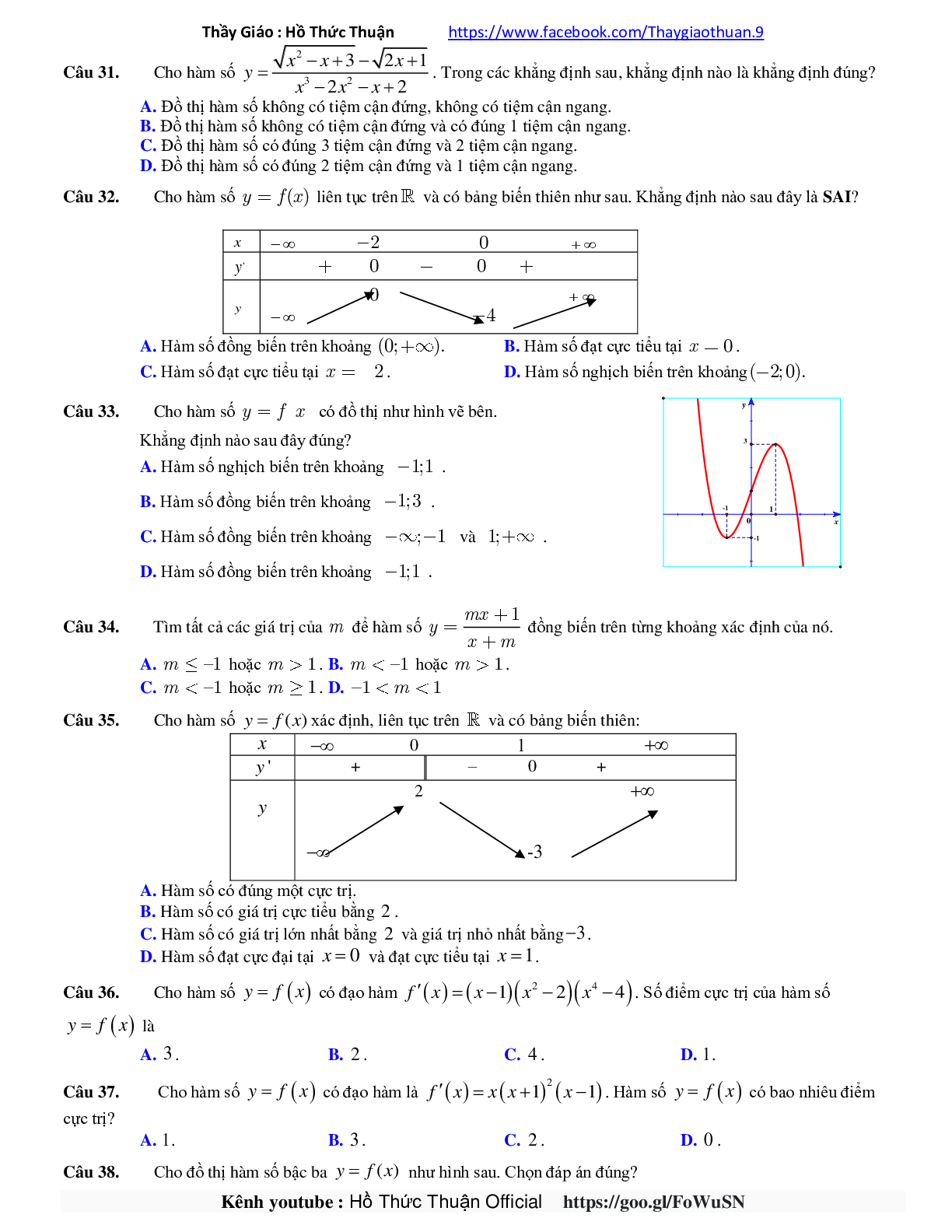
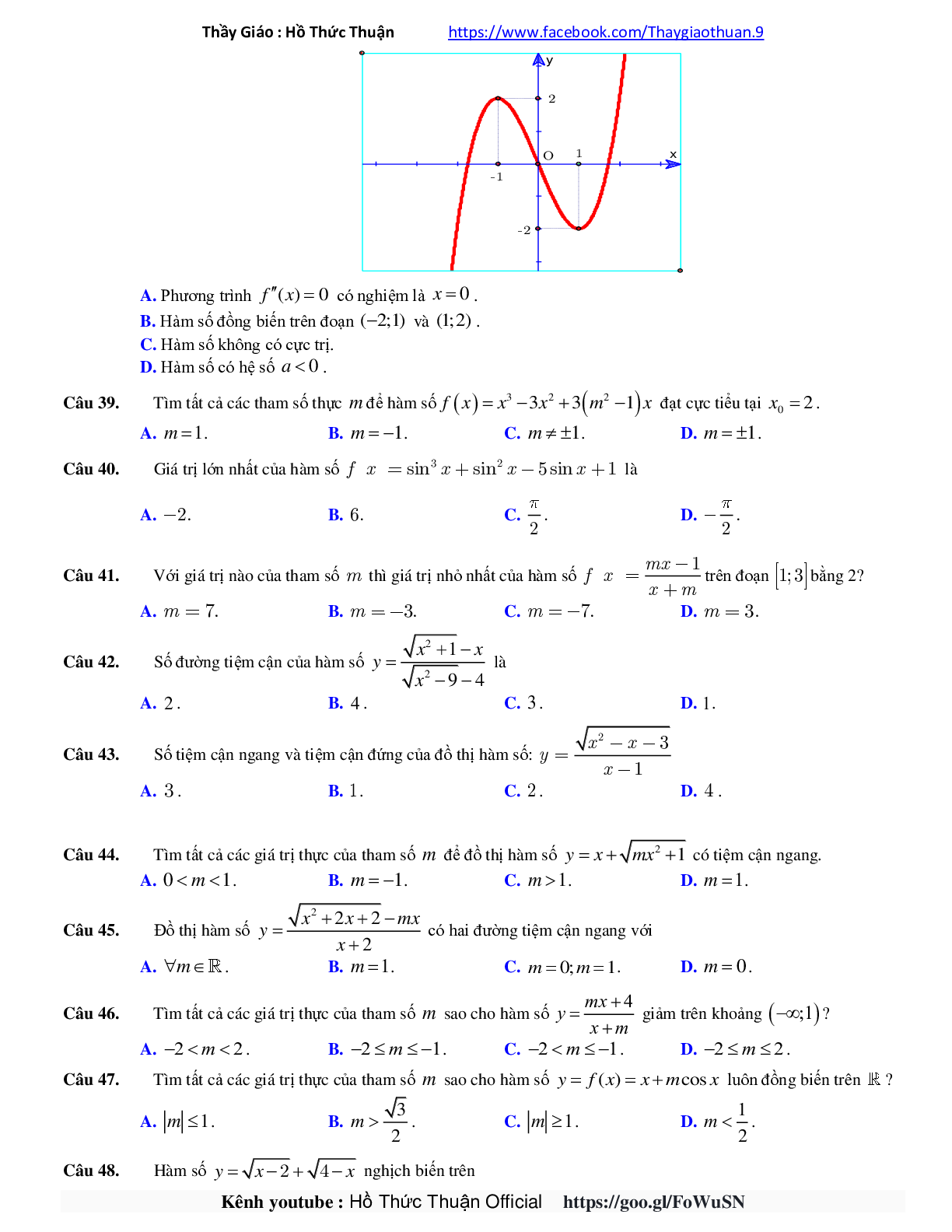
Câu 38. Cho đồ thị hàm số bậc ba y = f(x)  như hình sau. Chọn đáp án đúng?

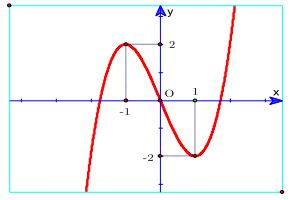
A. Phương trình \({f^{\prime \prime }}(x) = 0\) có nghiệm là x = 0.

B. Hàm số đồng biến trên đoạn (-2,1) và (1, 2).

C. Hàm số không có cực trị.

D. Hàm số có hệ số a < 0.

Câu 39. Tìm tất cả các tham số thực m để hàm số \(f(x) = {x^3} - 3{x^2} + 3\left( {{m^2} - 1} \right)x\) đạt cực tiểu tại \({x_0} = 2\).

A. \(m = 1\).

B. \(m =  - 1\).

C. \(m \ne  \pm 1\).

D. \(m =  \pm 1\).

Câu 40. Giá trị lớn nhất của hàm số \(fx = {\sin ^3}x + {\sin ^2}x - 5\sin x + 1\) là

A. \( - 2\).

B. 6 .

C. \(\frac{\pi }{2}\).

D. \( - \frac{\pi }{2}\).

Câu 41. Với giá trị nào của tham số m thì giá trị nhỏ nhât của hàm số \(fx = \frac{{mx - 1}}{{x + m}}\) trên đoạn [1 ; 3] bằng 2 ?

A. \(m = 7\).

B. \(m =  - 3\).

C. \(m =  - 7\).

D. \(m = 3\).

Câu 42. Số đường tiệm cận của hàm số \(y = \frac{{\sqrt {{x^2} + 1}  - x}}{{\sqrt {{x^2} - 9}  - 4}}\) là

A. 2 .

B. 4 .

C. 3 .

D. 1 .

Câu 43. Số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số: \(y = \frac{{\sqrt {{x^2} - x - 3} }}{{x - 1}}\)

A. 3 .

B. 1 .

C. 2 .

D. 4 .

Câu 44. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = x + \sqrt {m{x^2} + 1} \) có tiệm cận ngang.

A. \(0 < m < 1\).

B. \(m =  - 1\).

C. \(m > 1\).

D. \(m = 1\).

Câu 45. Đồ thị hàm số \(y = \frac{{\sqrt {{x^2} + 2x + 2}  - mx}}{{x + 2}}\) có hai đường tiệm cận ngang với

A. \(\forall m \in \mathbb{R}\).

B. \(m = 1\).

C. \(m = 0;m = 1\).

D. \(m = 0\).

Câu 46. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y = \frac{{mx + 4}}{{x + m}}\) giảm trên khoảng \(( - \infty ;1)\) ?

A. \( - 2 < m < 2\).

B. \( - 2 \le m \le  - 1\).

C. \( - 2 < m \le  - 1\).

D. \( - 2 \le m \le 2\).

Câu 47. Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y = f(x) = x + m\cos x\) luôn đồng biến trên \(\mathbb{R}\) ?

A. \(|m| \le 1\).

B. \(m > \frac{{\sqrt 3 }}{2}\).

C. \(|m| \ge 1\).

D. \(m < \frac{1}{2}\).

Câu 48. Hàm số \(y = \sqrt {x - 2}  + \sqrt {4 - x} \) nghịch biến trên

A. \([3;4)\).

B. \((2;3)\).

C. \((\sqrt 2 ;3)\).

D. \((2;4)\).

Câu 49. Các khoảng đồng biến của hàm số \(y = \frac{x}{{{x^2} + 1}}\) là

A. \( - \infty , - 1,1, + \infty \).

B. \(\mathbb{R}\backslash  - 1,1\).

C. -1;1.

D. \(\mathbb{R}\).

Câu 50. Các khoảng nghịch biến của hàm số \(y = \sqrt { - {x^2} + 2x} \) là

A. 1,2 .

B. 0,1 .

C. \( - \infty ,1;2, + \infty \).

D. [1,2].

Câu 51. Tìm tất cả các tham số thực m để hàm số \(y = \frac{1}{3}{x^3} + \left( {{m^2} - m + 2} \right){x^2} + \left( {3{m^2} + 1} \right)x + m - 5\) đạt cực tiểu tại \(x =  - 2.\)

A. \(m = 1\).

B. \(m = 0\).

C. \(m =  - 1\).

D. \(m = 3\).

Câu 52. Tìm tất cả các tham số thực m để hàm số \(y = {x^4} - 2(m + 1){x^2} + m\) có 3 cực trị

A. \(m \le  - 1\).

B. \(m <  - 1\).

C. \(m \ge  - 1\).

D. \(m >  - 1\).

Câu 53. Tìm tất cả các tham số thực m để hàm số \(y = m{x^3} - 3(m - 1){x^2} + 3(m + 1)x + m\) có cực trị.

A. \(m \in \left( { - \infty ;\frac{1}{3}} \right)\backslash \{ 0\} \).

B. \(m \in \left( { - \infty ;\frac{1}{3}} \right)\).

C. \(m > \frac{1}{3}\).

D. \(m < 1\).

Câu 54. Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x - {m^3}\). Điều kiện của m để hàm số có cực đại, cực tiểu và phương trình đường thẳng đi qua hai điểm cực trị là

A. \(m \in R,y =  - 2x + m\).

B. \(m \in R,y =  - 2x - m\).

C. \(m < 1,y =  - 2x + m\).

D. \(m > 1,y =  - 2x + m\).