Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển chọn 22 câu trắc nghiệm ôn tập đồ thị hàm hợp vận dụng cao 8+, phần đơn điệu và cực trị hàm số, tài liệu bao gồm 6 trang, 22 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Đồ thị hàm hợp vận dụng cao 8+ phần đơn điệu + cực trị hàm số

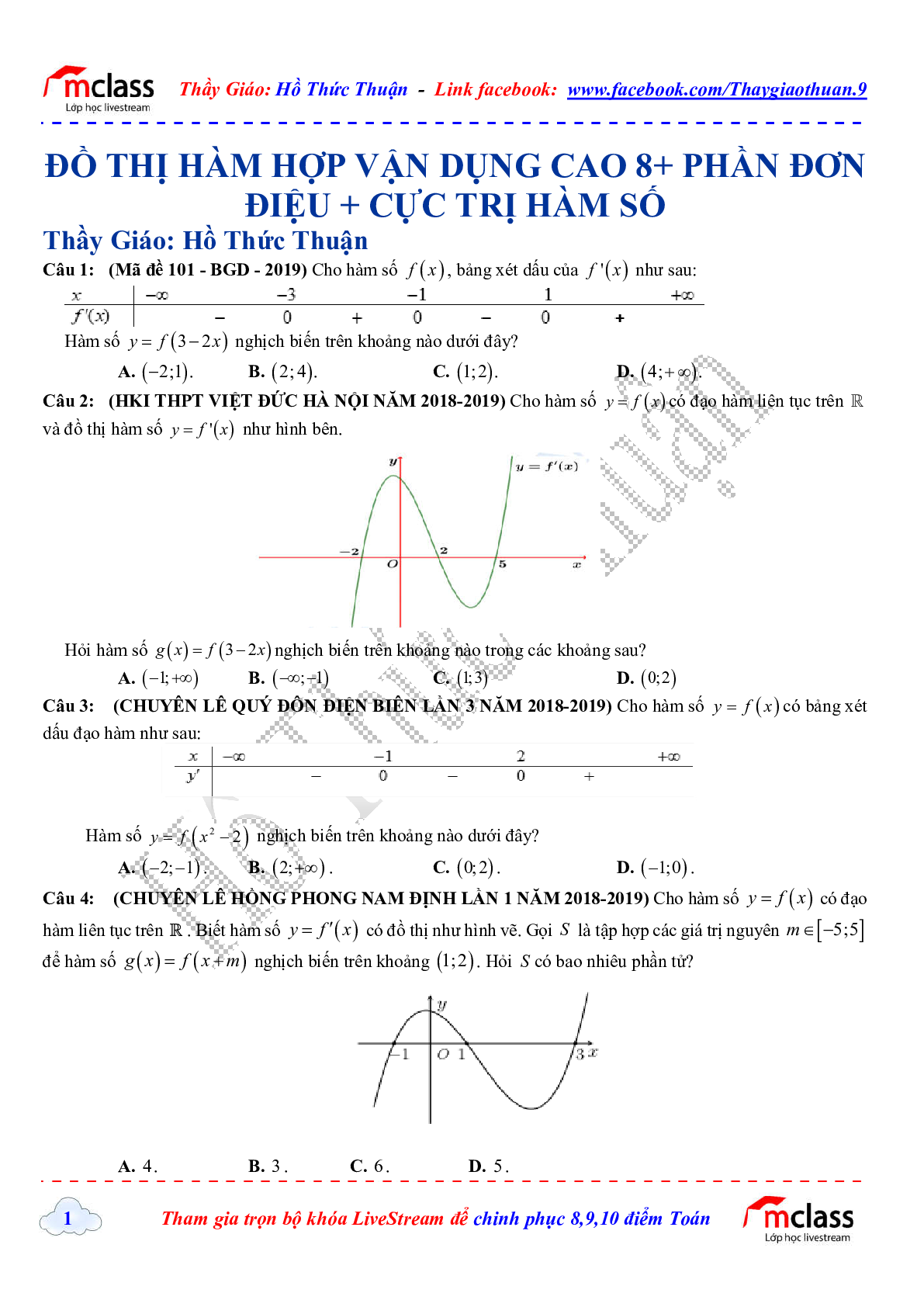
Câu 1: (Mã đề 101 - BGD - 2019) Cho hàm số f(x), bảng xét dấu của \({f^\prime }(x)\) như sau:

Hàm số y = f(3-2 x) nghịch biến trên khoảng nào dưới đây?

A. (-2;1).

B. ( 2;4).

C. (1;2).

D. \((4; + \infty )\).

Câu 2: (HKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hàm số y = f(x) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = {f^\prime }(x)\) như hình bên.

Hỏi hàm số \(g(x) = f(3 - 2x)\) nghịch biến trên khoảng nào trong các khoảng sau?

A. \(( - 1; + \infty )\)

B. \(( - \infty ; - 1)\)

C. (1;3)

D. (0; 2)

Câu 3: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau:

Hàm số  \[y = f\left( {{x^2} - 2} \right)\]nghịch biến trên khoảng nào dưới đây?

A. ( - 2; -1).

B. \((2; + \infty )\).

C. (0; 2).

D. ( -1;0).

Câu 4: (CHUYÊN LÊ HỒNG PHONG NAM ĐINH LẦN 1 NĂM 2018-2019) Cho hàm số y = f(x) có đạo hàm liên tục trên \(\mathbb{R}\). Biết hàm số \(y = {f^\prime }(x)\) có đồ thị như hình vẽ. Gọi \(S\) là tập hợp các giá trị nguyên \(m \in [ - 5;5]\) để hàm số \(g(x) = f(x + m)\) nghịch biến trên khoảng (1;2). Hỏi S có bao nhiêu phần tử?

A. 4

B. 3 .

C. 6

D. 5 .

Câu 5: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau

Hàm số \[y = 3f(x + 2) - {x^3} + 3x\]đồng biến trên khoảng nào dưới đây?

A. \(( - \infty ; - 1)\).

B. (-1;0).

C. (0;2).

D. \((1; + \infty )\).

Câu 6: (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau

Hàm số  \[y = f(x - 1) + {x^3} - 12x + 2019\]nghịch biến trên khoảng nào dưới đây?

A. \((1; + \infty )\).

B. (1;2).

C. \(( - \infty ;1)\).

D. (3;4).

Câu 7: (CHUYÊN PHAN BỘI CHÂU NGHỆ AN LẦN 1 NĂM 2018-2019) Cho hàm số f(x) có bảng xét dấu đạo hàm như sau:

Hàm số \[y = 2f(1 - x) + \sqrt {{x^2} + 1}  - x\] nghịch biến trên những khoảng nào dưới đây

A. \(( - \infty ; - 2)\).

B. \(( - \infty ;1)\).

C. ­(-2;0).

D. (-3;-2).

Câu 8: (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau

Hàm số \[y =  - 2f(x) + 2019\] nghịch biến trên khoảng nào trong các khoảng dưới đây?

A. (-4;2).

B. (-1;2).

C. (-2;-1).

D. (2;4).

Câu 9: (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Cho hàm số bậc bốn y = f(x) có đồ thị của hàm số \(y = {f^\prime }(x)\) như hình vẽ bên.

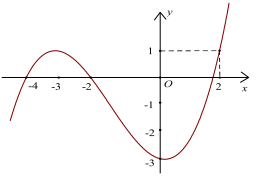
Hàm số \(y = 3f(x) + {x^3} - 6{x^2} + 9x\) đồng biến trên khoảng nào trong các khoảng sau đây?

A. (0;2).

B. (-1;1).

C. \((1; + \infty )\).

D. (-2;0).

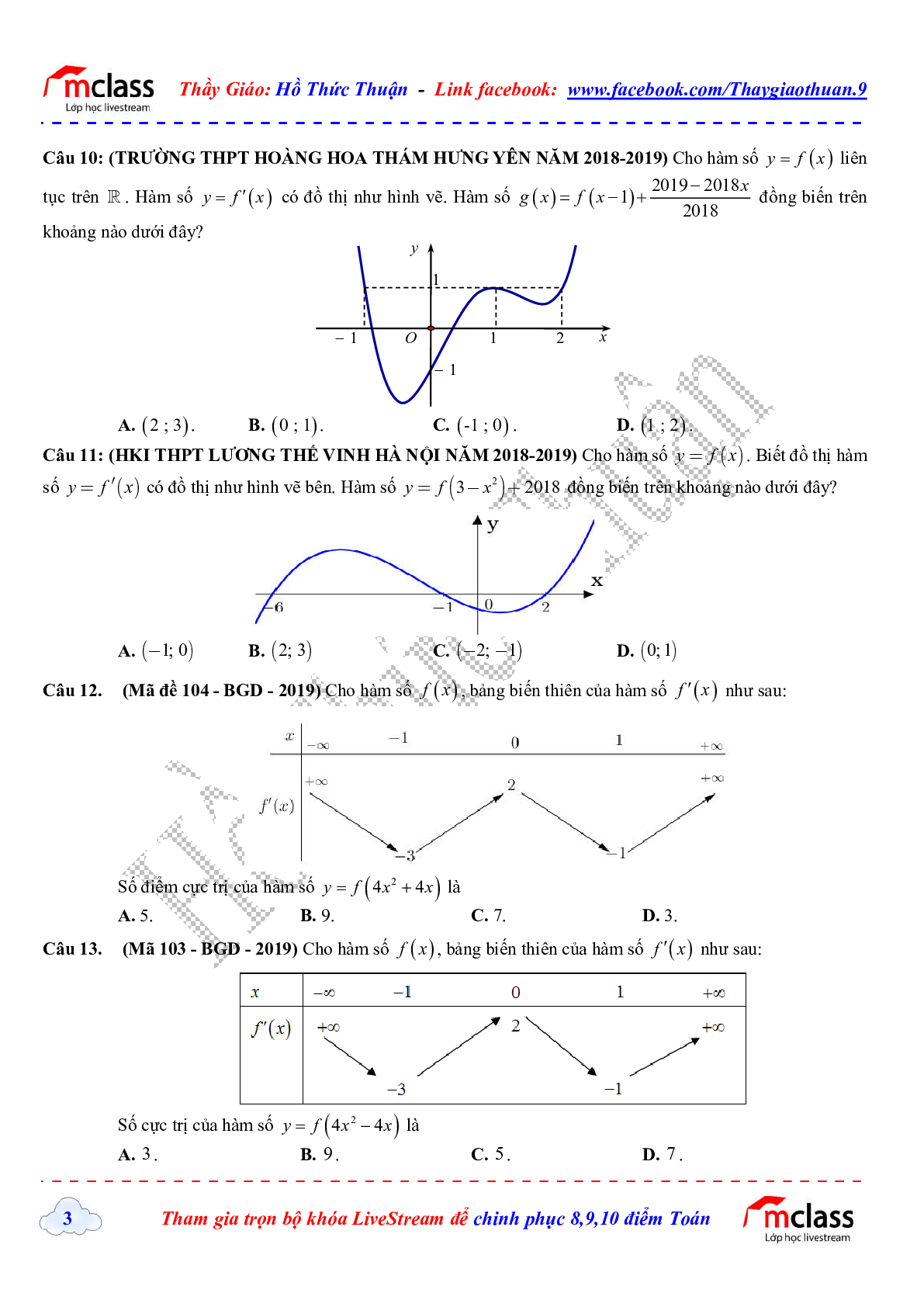
Câu 10: (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\). Hàm số \(y = {f^\prime }(x)\) có đồ thị như hình vẽ. Hàm số \(g(x) = f(x - 1) + \frac{{2019 - 2018x}}{{2018}}\) đồng biến trên khoảng nào dưới đây?

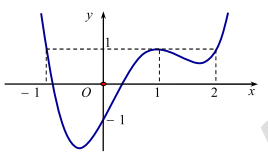
A. (2;3).

B. (0;1)

C. (-1;0).

D. (1;2).

Câu 11: (HKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hàm số y = f(x). Biết đồ thị hàm số \(y = {f^\prime }(x)\) có đồ thị như hình vẽ bên. Hàm số \(y = f\left( {3 - {x^2}} \right) + 2018\) đồng biến trên khoảng nào dưới đây?

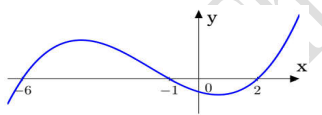
A. (-1;0).

B. (2;3).

C. (-2;-1).

D. (0;1)

Câu 12. (Mã đề 104 - BGD - 2019) Cho hàm số f(x), bảng biến thiên của hàm số \({f^\prime }(x)\) như sau:

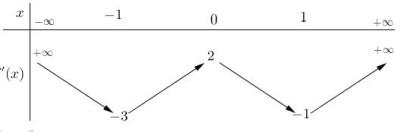
Số điểm cực trị của hàm số \[y = f\left( {4{x^2} + 4x} \right)\] là

A. 5

B. 9 .

C. 7 .

D. 3 .

Câu 13. (Mã đề 103 - BGD - 2019) Cho hàm số f(x), bảng biến thiên của hàm số \({f^\prime }(x)\) như sau:

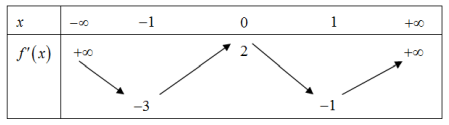
Số cực trị của hàm số \(y = f\left( {4{x^2} - 4x} \right)\) là

A. 3 .

B. 9 .

C. 5 .

D. 7 .

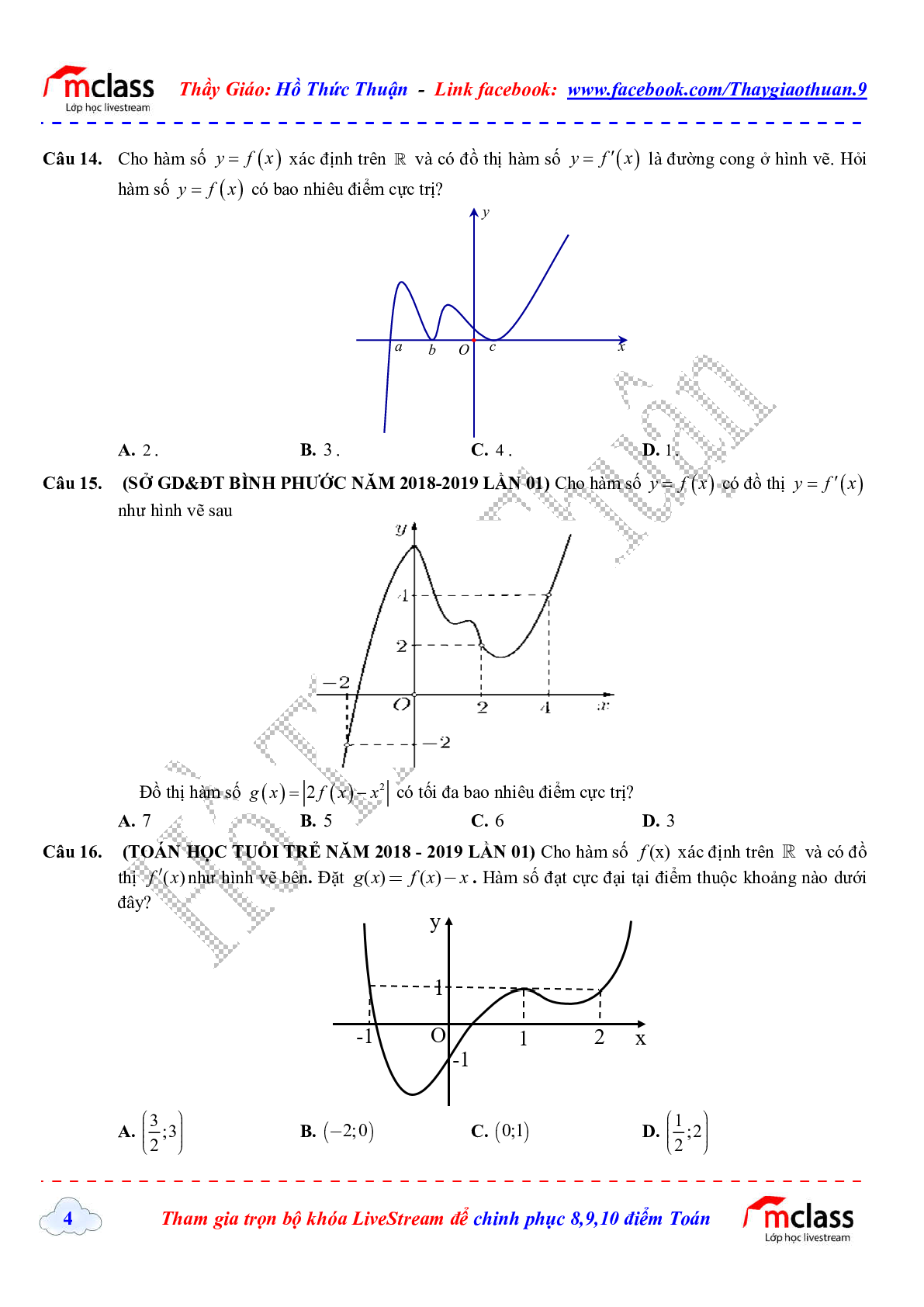
Câu 14. Cho hàm số y = f(x) xác định trên \(\mathbb{R}\) và có đồ thị hàm số \(y = {f^\prime }(x)\) là đường cong ở hình vẽ. Hỏi hàm số y = f(x)  có bao nhiêu điểm cực trị?

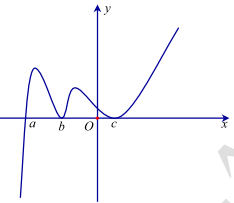
A. 2 .

B. 3 .

C. 4 .

D. 1 .

Câu 15. (SỞ GD\&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số y = f(x) có đồ thị \(y = {f^\prime }(x)\) như hình vẽ sau

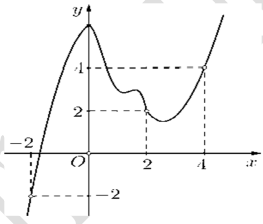
Đồ thị hàm số \(g(x) = \left| {2f(x) - {x^2}} \right|\) có tối đa bao nhiêu điểm cực trị?

A. 7

B. 5

C. 6

D. 3

Câu 16. (TOÁN HỌC TUỔI TRẺ̉ NĂM 2018 - 2019 LẦN 01) Cho hàm số f(x) xác định trên \(\mathbb{R}\) và có đồ thị \({f^\prime }(x)\) như hình vẽ bên. Đặt \(g(x) = f(x) - x\). Hàm số đạt cực đại tại điểm thuộc khoảng nào dưới đây?

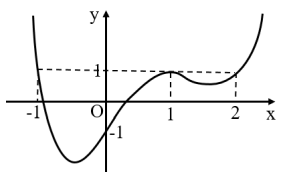
A. \(\left( {\frac{3}{2};3} \right)\)

B. (-2;0)

C. (0;1)

D. \(\left( {\frac{1}{2};2} \right)\)

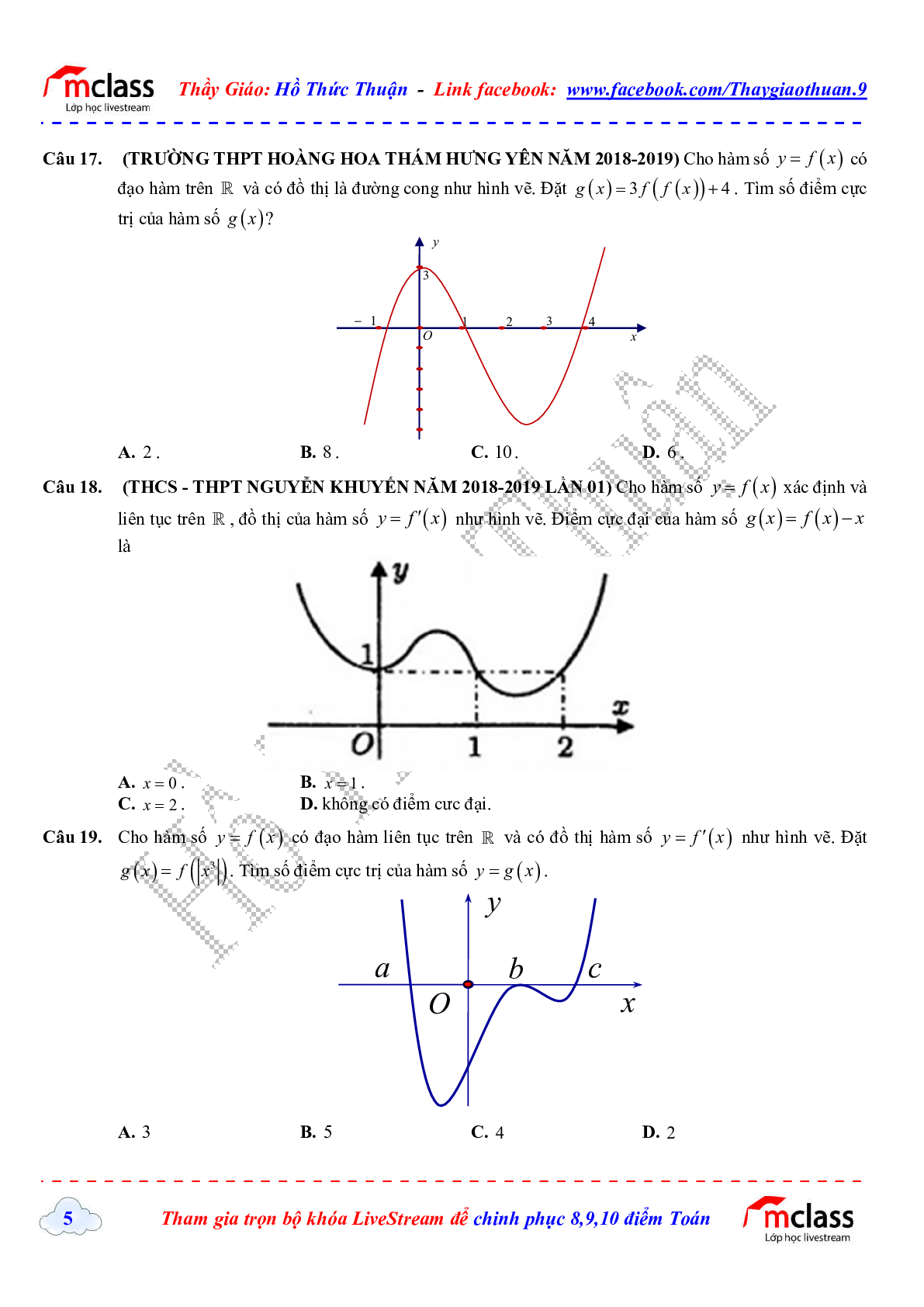
Câu 17. (TRƯỜG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hàm số y = f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ. Đặt \(g(x) = 3f(f(x)) + 4\). Tìm số điểm cực trị của hàm số g(x) ?

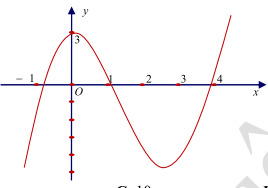
A. 2 .

B. 8 .

C. 10 .

D. 6 .

Câu 18. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y = f(x) xác định và liên tục trên \(\mathbb{R}\), đồ thị của hàm số \(y = {f^\prime }(x)\) như hình vẽ. Điểm cực đại của hàm số \(g(x) = f(x) - x\) là

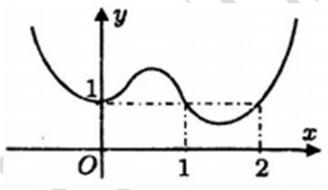
A. \(x = 0\).

B. \(x = 1\).

C. \(x = 2\).

D. không có điểm cưc đại.

Câu 19. Cho hàm số y = f(x) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = {f^\prime }(x)\) như hình vẽ. Đặt \(g(x) = f\left( {\left| {{x^3}} \right|} \right)\). Tìm số điểm cực trị của hàm số y = g(x).

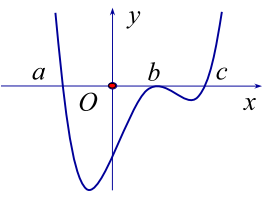
A. 3

B. 5

C. 4

D. 2

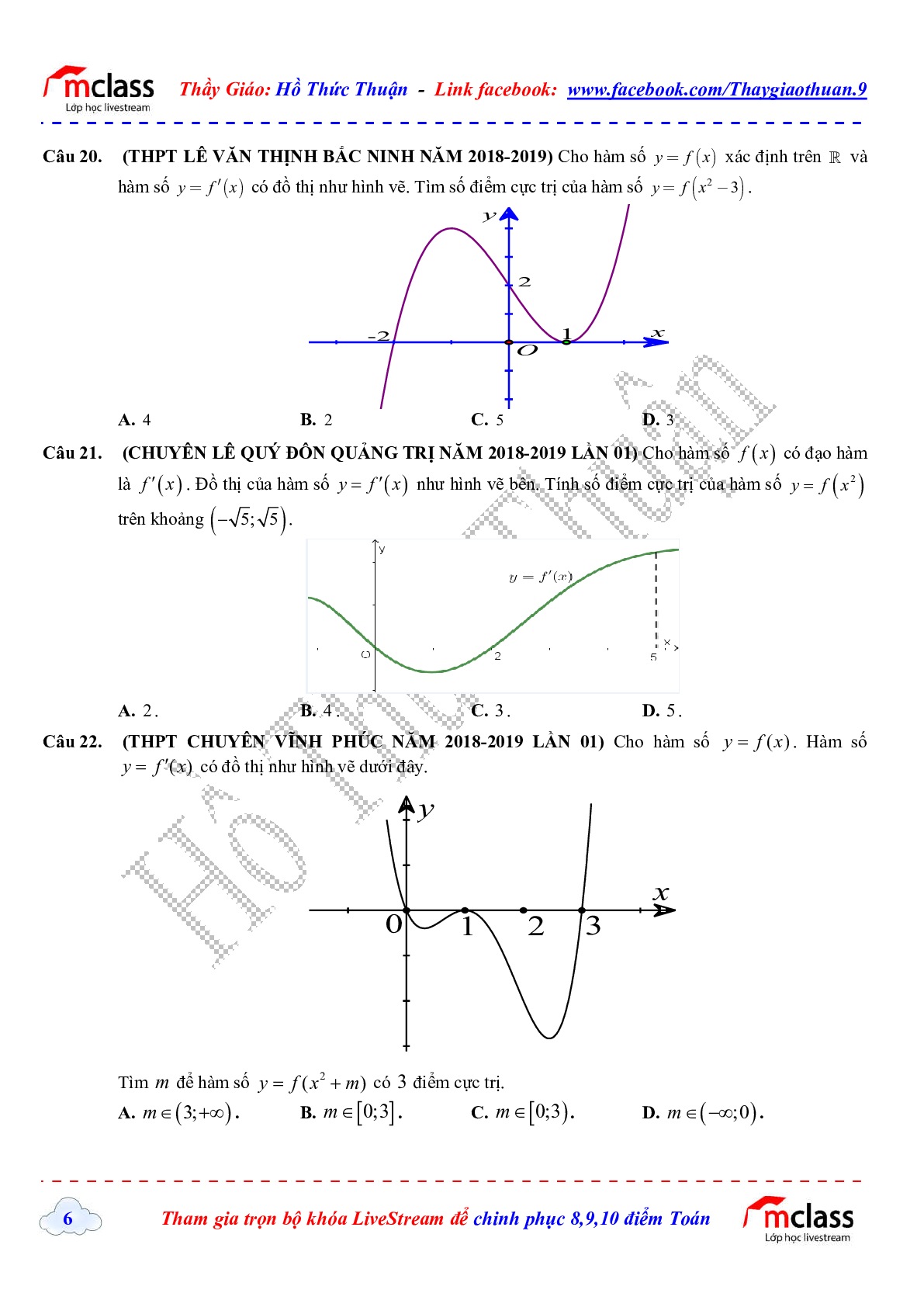
Câu 20. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\) và hàm số \(y = {f^\prime }(x)\) có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số \(y = f\left( {{x^2} - 3} \right)\).

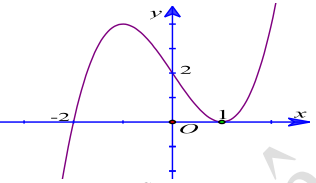
A. 4

B. 2

C. 5

D. 3

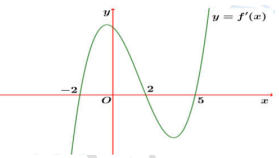
Câu 21. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hàm số f(x) có đạo hàm là \({f^\prime }(x)\). Đồ thị của hàm số \(y = {f^\prime }(x)\) như hình vẽ bên. Tính số điểm cực trị của hàm số \(y = f\left( {{x^2}} \right)\) trên khoảng \(( - \sqrt 5 ;\sqrt 5 )\).

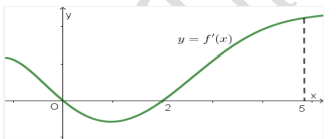
A. 2 .

B. 4 .

C. 3 .

D. 5 .

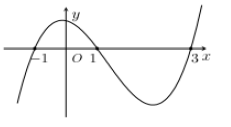
Câu 22. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hàm số y = f(x). Hàm số \(y = {f^\prime }(x)\) có đồ thị như hình vẽ dưới đây.

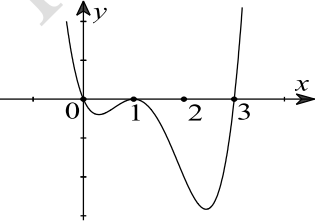
Tìm m để hàm số \(y = f\left( {{x^2} + m} \right)\) có 3 điểm cực trị.

A. \(m \in (3; + \infty )\).

B. \(m \in [0;3]\).

C. \(m \in [0;3)\).

D. \(m \in ( - \infty ;0)\).